1変数関数y=f(x)=x2の性質　：トピック一覧　　　
・グラフ/増減/値域/有界性/最大最小/逆像(平方根および√)/単射/全射/全単射/逆関数/極限/連続/極大極小　
・平方根と√の定義　
※1変数関数の具体例：y=x /  y=x3 / y=1/x  → 自然数指数の冪関数/整数指数のべき関数/有理数指数のべき関数/実数指数のべき関数
　　　　　　　　　　 定数値関数/比例/一次関数/二次関数/三次関数→多項式関数　　
　　　　　　　　　　　指数関数/対数関数　
　　　　　　　　　　　絶対値関数/三角関数　/ガンマ関数
※1変数関数に関する諸概念の定義：1変数関数一般の定義/極限/連続性/微分/定積分/広義積分/スチルチェス積分
※関数定義関連ページ：2変数関数/n変数関数/実数値関数一般/ベクトル値関数/写像一般
※総目次

  y=f(x)= x2



グラフ

 ・R＝(−∞,∞）で定義された1変数関数y=f (x)=x2のグラフは、
　・原点(0,0)でx軸に接する
　・下に凸な　
　・R2上の放物線
　である。　　




[文献]
　中学生向けの教科書で、お馴染み。
　あえて、文献をあげると、

　・松坂『解析入門1』3.1-D(p.100);








y=x~2のグラフ

・[0,∞)で定義された1変数関数y=f (x)= x2のグラフ
y=x^2の[0,∞)への制限

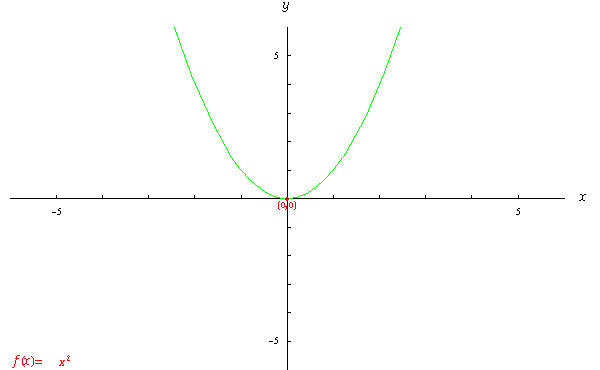
・「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」の(-∞,0]への制限
　　すなわち、「(−∞,0]で定義された1変数関数y=f (x)= x2」のグラフ


→[トピック一覧:y=f(x)=x2の性質]
→総目次

  y=f(x)= x2の増減
　 ・R＝(−∞,∞）で定義された1変数関数y=f (x)= x2は、
　　　　　　　　(−∞,＋∞)における単調関数ではない。y=x~2のグラフ




[文献]
　中学生向けの教科書で、お馴染み。
　あえて、文献をあげると、

　・松坂『解析入門1』3.1-D(p.100);



　

・「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」の(-∞,0]への制限（すなわち、「(−∞,0]で定義された1変数関数y=f (x)= x2」）　
　　は、狭義単調減少関数。
　　　　　

・「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」の[0,∞)への制限（すなわち、「[0,∞)で定義された1変数関数y=f (x)= x2」）
　　は、狭義単調増加関数。
　　　　　y=x^2の[0,∞)への制限

→[トピック一覧:y=f(x)=x2の性質]
→総目次


　 y=f(x)= x2の値域
　 ・R＝(−∞,∞）で定義された1変数関数y=f (x)= x2の値域は、[0,∞) 。
y=x~2のグラフ

・「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」の(-∞,0]への制限（すなわち、「(−∞,0]で定義された1変数関数y=f (x)= x2」）　
　　の値域も、[0,∞) 。

　　　

・「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」の[0,∞)への制限（すなわち、「[0,∞)で定義された1変数関数y=f (x)= x2」）　
　　の値域も、[0,∞) 。

　　　y=x^2の[0,∞)への制限





y=f(x)= x2は非有界
　 ・R＝(−∞,∞）で定義された1変数関数y=f (x)= x2は、下に有界だが、上に有界ではないので、
　　　　　　　　　　　有界でない。

y=f(x)= x2の最大値・最小値
　 ・R＝(−∞,∞）で定義された1変数関数y=f (x)= x2のR＝(−∞,∞）における最大値は、
　　存在しない。
・R＝(−∞,∞）で定義された1変数関数y=f (x)= x2のR＝(−∞,∞）における最小値はf(0)＝0。
　　

→[トピック一覧:y=f(x)=x2の性質]
→総目次


y=f(x)= x2による逆像、平方根、√

　※一般化：y=x3による逆像/べき関数y=xnによ る逆像




[文献]
　・『岩波数学入門辞典』平方根(p.543)
　・吉田栗田戸田『高等学校数学I』(p.53)
　　　上記2文献では、「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」による実数yの逆像を平方根と呼び、
　　　実数y>0のとき、二つある平方根のうち、正のほうを√yで表すとしている。
　・小平『解析入門I』§2.3-a) (p.89);n乗根一般。
　・ 松坂『解析入門1』3.2E-例(p.113);n乗根一般。

　・赤攝也『実数論講義』§6.5定義6.5.3(p.197)　

[解説]

・左図からわかるように、
　　R＝(−∞,∞）で定義された1変数関数y=f (x)= x2　に関しては、
　　　(i)任意の正の実数yに対して、
　　　　　yのfによる逆像 f−1(y)は、「2個の実数」からなる。
　　　(ii)y=0に対して、
　　　　　y=0のfによる逆像 f−1(y)は、「1個の実数0」のみからなる。
　　　(iii)任意の負の実数yに対して、
　　　　　yのfによる逆像 f−1(y)は、空集合。
　となるので、
　「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」は、単射ではない。
　したがって、「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」には、逆関数は存在しない。

「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」による、y= の逆像(平方根)。

y=f(x)=xによる逆像


「[0,∞)で定義された1変数関数y=f (x)= x2」による、y= の逆像(√y)。
y=f(x)=x^2による逆像
 ・ところが、「[0,∞)で定義された1変数関数y=f (x)= x2」に関しては、
　　　(i)任意の非負の実数yに対して、
　　　　　yのfによる逆像 f−1(y)は、「1個の実数」からなる。
　　　(ii)任意の負の実数yに対して、
　　　　　yのfによる逆像 f−1(y)は、空集合。
　つまり、「[0,∞)で定義された1変数関数y=f (x)= x2」は、
　　　　　単射。
　したがって、「[0,∞)で定義された1変数関数y=f (x)= x2」には、
　逆関数が存在する。

・「正の実数yの『[0,∞)で定義された1変数関数y=f (x)= x2』による逆像」を、　
　　　　　　　記号　 
y 
　または、　y1/2 　　　　
　　で表す。

・「[0,∞)で定義された1変数関数y=f (x)= x2」の逆関数「[0,∞)で定義された1変数関数x　=　f-1(y)」を、
　　　　x=f-1(y)＝ 
y 
　または、　x=f-1(y)＝y1/2 　
　　で表す。

※√を一般化した概念→  3√ / n√　

→[トピック一覧:y=f(x)=x2の性質]
→総目次


y=f(x)= x2　と全単射

・R＝(−∞,∞）で定義された1変数関数y=f (x)= x2は、単射ではない。
　※な ぜ？→下図をいじるとわかるように、
　　　　　　任意の正の実数yに対して、
　　　　　　yのfによる逆像 f−1(y)は 「2個の実数」からなるので。
　[図]　(−∞,∞）で定義された1変数関数y=f (x)= x2による、y= の逆像。

y=f(x)=x^2による逆像

・R＝(−∞,∞）で定義された1変数関数y=f (x)= x2は、Rの上への全射ではないが、
　　　　　　　　　　　　　　　　　　　　　　　　[0,∞)の上への全射ではある。






【関連事項】
　・定義の確認→1変数関数が単射/全射/全単射　
　・類例の参照→y=xの全単射の検討/y=x3の全単射の検討
　・一般化した事例の参照→自然数指数の累乗関数の全単射の検討
　　　　　　　　　　　　整数指数の累乗関数の全単射の検討　
　　　　　　　　　　　　有理数指数の累乗関数の全単射の検討　

【文献】

　・黒田『微分積分学』3.1.2-例3.2(pp.86-7)
　・ラング『ラング現代微積分学』0章§2例3(p.6)　






・[0,∞)で定義された1変数関数y=f (x)= x2は単射になる。
　※な ぜ？→下図をいじるとわかるように、
　　　　　　ど のように、実数yを 選んでも、
　　　　　　　　　実数yのfによる逆像 f−1(y)が 「1個の実数」からなる
　　　　　　　　　または、
　　　　　　　　　実数yのfによる逆像 f−1(y)は空集合　
　　　　　　となるから。
　　[図]「[0,∞)で定義された1変数関数y=f (x)= x2」による、y= の逆像。
y=f(x)=x^2による逆像
・[0,∞)で定義された1変数関数y=f (x)= x2は、Rの上への全射ではないが、
　　　　　　　　　　　　　　　　　　　　　[0,∞)の上への全射ではある。
・だから、
　　y=f (x)= x2を対応規則とする「f:[0,∞)→R」は、全単射にならないものの、
　　y=f (x)= x2を対応規則とする「f:[0,∞)→[0,∞)」は、全単射になっている。
・(−∞,0]で定義された1変数関数y=f (x)= x2は単射になる。
　(−∞,0]で定義された1変数関数y=f (x)= x2はRの上への全射ではないが、
　　　　　　　　　　　　　　　　　　　　　[0,∞)の上への全射ではある。
　だから、
　　y=f (x)= x2を対応規則とする「f:(−∞,0]→R」は、全単射にならないものの、
　　y=f (x)= x2を対応規則とする「f:(−∞,0]→[0,∞)」は、全単射になっている。




[文献]
　・加藤十吉『微分積分学原論』4.3-例9:2次関数(pp.36-7)
　・『解析演習ハンドブック1変数関数編』ex.1.1.12(p.11)　




→[トピック一覧:y=f(x)=x2の性質]
→総目次

　y=f(x)=x2の逆対応、逆関数、平方根の定義
→[R＝(−∞,∞）で定義された1変数関数y=f (x)= x2の逆関数]
→[[0,∞）で定義された1変数関数y=f (x)= x2の逆関数と√の定義]
→[(−∞,0]で定義された1変数関数y=f (x)= x2の逆関数]

※1変数関数の「逆関数（の存在）」定義
※1変数関数の具体例の「逆関数（の存在）」について：
　　　定数値関数/y=x/比例/一次関数/反比例/二次関数/べき関数
　　　指数関数/対数関数/絶対値関数/三角関数/ガンマ関数

R＝(−∞,∞）で定義された1変数関数y=f (x)= x2の逆対応・逆関数

[逆関数の存在の有無]

・「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」は単射でないから、
　「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」の逆対応は、
　　　関数の定義を満たしていない。
　　すなわち、
　　R＝(−∞,∞）で定義された1変数関数y=f (x)= x2の逆関数は存在しない。

[文献]

　・青本『微分と積分1』例1.49(p.34);例1.81(p.48):[0,∞)で定義された1変数関数y=f (x)= x2の逆関数について。証明なし.
　・小平『解析入門I』§2.3-a) (p.89);n乗根一般。
  ・ 松坂『解析入門1』3.2E-例(p.113);n乗根一般。
　・赤攝也『実数論講義』§6.5定義6.5.3(p.197):。
  ・『岩波数学入門辞典』平方根(p.543)
  ・『高等学校　数学I』(p.53)

[解説]

　・「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」のグラフを、
　　　通常とは逆に、
　　　　　「yの値を一つ決めて、それに対応するxの値(yの値の逆像)を読み取る」
　　　という方向で読み取れば(→右図)、
　　　「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」の逆対応「x　=　f-1(y)」のグラフ
　　　となる。
　・ 同一のyの値に、複数のxの値が対応付けられていることから、
　　「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」の逆対応　「x　=　f-1(y)」は、
　　　1変数関数の定義を満たしていない
　　　〜つまり、R＝(−∞,∞）で定義された1変数関数y=f (x)= x2に逆関数は存在しない〜
　　　と分かる。

[図：「y=x2のグラフ」を「逆対応のグラフ」として読む]

「R＝(−∞,∞）で定義された1変数関数y=f (x)= x2」の逆対応「x　= 　f-1(y)」
　　　　　　 y= に対応するx　=　f-1(y)の 値は…?　

y=f(x)=x^2による逆像

　・R＝(−∞,∞）で定義された1変数関数y=f (x)= x2の逆対応「x　=　f-1(y)」を、
　　慣例に従って、x,yを入れ替えて、
　　　　　　y=g(x)=　f-1(x)＝ ±√x　
　　としたグラフが下図。
　　同一のxの値に、複数のyの値が対応付けられており、関数の定義を満たしていない。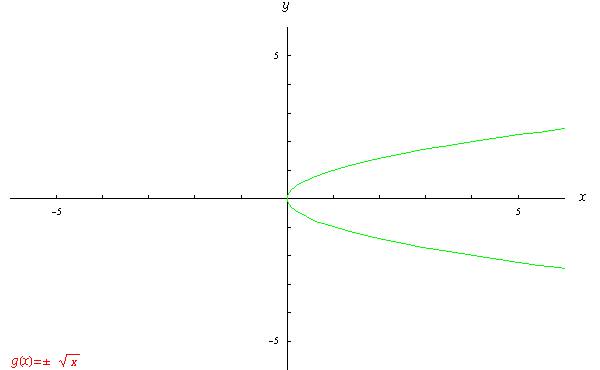
y=^2の逆対応

　　したがって、R＝(−∞,∞）で定義された1変数関数y=f (x)= x2の逆関数は存在しない。


[0,∞)で定義された1変数関数y=f (x)= x2の逆関数




[文献]
　・青本『微分と積分1』例1.49(p.34);例1.81(p.48):[0,∞)で定義された1変数関数y=f (x)= x2の逆関数について。証明なし.
　・小平『解析入門I』§2.3-a) (p.89);n乗根一般。
  ・ 松坂『解析入門1』3.2E-例(p.113);n乗根一般。
　・赤攝也『実数論講義』§6.5定義6.5.3(p.197):。
  ・『岩波数学入門辞典』平方根(p.543)
  ・『高等学校　数学I』(p.53)　




[0,∞)で定義された1変数関数y=f (x)= x2を考える(→下図)。
　　y=x^2の[0,∞)への制限

[逆関数の存在の有無]

・「[0,∞)で定義された1変数関数y=f (x)= x2」は単射になるので、
　「[0,∞)で定義された1変数関数y=f (x)= x2」の逆対応は、
　　　関数の定義を満たす。
　　すなわち、
　　　「[0,∞)で定義された1変数関数y=f (x)= x2」には、逆関数が存在する。

[逆関数の定義域]

・「[0,∞)で定義された1変数関数y=f (x)= x2」の値域は[0,∞) だから、
　「[0,∞)で定義された1変数関数y=f (x)= x2」の逆関数は、
　「[0,∞)で定義された1変数関数x=　f-1(y)」となる。

[逆関数の表現]

・「正の実数yの『[0,∞)で定義された1変数関数y=f (x)= x2』による逆像」は、
　　　　　　　記号　 
y 
　または、　y1/2 　　　　
　　で表される。
　　したがって、
　　「[0,∞)で定義された1変数関数y=f (x)= x2」の逆関数
　　　　　　　「[0,∞)で定義された1変数関数x　=　f-1(y)」
　　は、
　　　　x=f-1(y)＝ 
y 
　または、　x=f-1(y)＝y1/2 　
　　と表される。　

[ [0,∞）で定義された1変数関数y=f (x)= x2の逆関数のグラフ]

・「[0,∞)で定義された1変数関数y=f (x)= x2」のグラフを、
　　　通常とは逆に、
　　　「yの値を一つ決めて、それに対応するxの値(yの値の逆像)を読み取る」
　　という方向で読み取ると(→右図)、
　　「[0,∞)で定義された1変数関数y=f (x)= x2」の逆関数　x=f-1(y)＝ 
y 
のグラフ　
　　となる。
・慣例に従って、
　　「[0,∞)で定義された1変数関数y=f (x)= x2」の逆関数　x=f-1(y)＝ 
y 

　のx,yを入れ替えて、
　　y=f-1(x)＝ 
x 

　としたグラフが下図。
y=x^2の[0,∞)への制限の逆関数

[図：「y=x2のグラフ」を「逆関数のグラフ」として読む]

　　　　「[0,∞)で定義された1変数関数y=f (x)= x2」による、y= の逆像は…？
y=f(x)=x^2による逆像


（−∞,0]で定義された1変数関数y=f (x)= x2の逆関数

(−∞,0]で定義された1変数関数y=f (x)= x2を考える(→下図)。
　　　　

　・(−∞,0]で定義された1変数関数y=f (x)= x2は単射になるので、逆関数が存在する。
　　(−∞,0]で定義された1変数関数y=f (x)= xの逆関数は、
　　　　　　[0,∞)で定義された1変数関数x=g(y)= −√y　。
　　　　　　慣例に従って、x,yを入れ替えると、
　　　　　　[0,∞)で定義された1変数関数y=g(x)= −√x　。
　　　　　　このグラフは、下図。




→[トピック一覧:y=f(x)=x2の性質]
→総目次


y=f(x)=x2の極限
　 ・R＝(−∞,∞）で定義された1変数関数y=f (x)= x2は、
　　　　どんな実数aに対しても、　f(x)→a2 (x→a)　
※なぜ？
　　・y=g(x)=xの極限の性質より、
      y=g(x)= xは、
　　　　　どんな実数aに対しても、　g(x)→a (x→a)。
　　・「関数どおしの積」の極限は、「関数の極限」どおしの積となるという定理と、
　　　　上記で得られた「g(x)の極限値」より、
　　　　　　　　　　　g(x)2→a2 (x→a)
　　　・したがって、f (x)=g(x)2= x2は、
　　　　どんな実数aに対しても、　f(x)→a2(x→a)　。		 　


【関連事項】
・1変数関数の極限定義
・1変数関数の具体例の極限：
　　　定数値関数/y=x/比例/一次関数/反比例/二次関数/べき関数
　　　指数関数/対数関数/絶対値関数/三角関数/ガンマ関数

【文献】
　・吉永『初等解析学:実数+イプシロンデルタ+積分』例3.1.5(p.109）:
　　　　　・多項式関数一般に関して。
　　　　　・定数関数の極限、f(x)=xの極限と、関数の極限の和積による証明つき。
　・黒田『微分積分学』3.3.2-例3.16(p.102):「任意の多項式はRで連続」。
　　・証明として、
　　　定数関数とf(x)=xがRで連続だから、連続関数の和差積・定数倍も連続関数より。






→[トピック一覧:y=f(x)=x2の性質]
→総目次

  y=f(x)=x2の連続性
　 ・R＝(−∞,∞）で定義された1変数関数y=f (x)= x2は、
　　　　　R＝(−∞,∞）上の連続関数。
※なぜ？
　・y=f (x)= x2という定義より、どんな実数aに対しても、f(a)= a2
　・y=f(x)=x2の極限の性質より、どんな実数aに対しても、　f(x)→a2(x→a)
　・以上二点より、どんな実数aに対しても、　f(x)→f(a) (x→a)　
　　　つまり、R＝(−∞,∞）で定義された1変数関数y=f (x)= x2は、
　　　　　　　　　どんな実数aにおいても、連続性の定義を満たす。
　　したがって、
　　　R＝(−∞,∞）で定義された1変数関数y=f (x)= x2は、
　　　　　R＝(−∞,∞）上の連続関数。　　　　




【関連事項】
　・1変数連続関数の定義
　・1変数関数の具体例の連続性：
　　　定数値関数/y=x/比例/一次関数/反比例/二次関数/べき関数
　　　指数関数/対数関数/絶対値関数/三角関数/ガンマ関数
【文献】
　・黒田『微分積分学』3.3.2-例3.16(p.102):「任意の多項式はRで連続」。
　　　→証明：定数値関数の連続性・y=f(x)=xの連続性、連続関数の和積定数倍も連続
　・吉永『初等解析学:実数+イプシロンデルタ+積分』例3.2.7(p.115）:多項式一般。
　　　　　　　　・証明：多項式関数の極限の性質より。
　・小林昭七『微分積分読本:1変数』第2章-1(p.38):多項式一般。証明:
　　　→証明：定数値関数の連続性・y=f(x)=xの連続性、連続関数の和積も連続



　

→[トピック一覧:y=f(x)=x2の性質]
→総目次


　
1変数定数値関数の導関数