実数値関数とその属性･類型：トピック一覧　　

　・定義：実数値関数
　・定義：実数値関数の定義域/像･値/値域/逆像･原像/実数値関数の最大値･最大点･最小値･最小点　
　・定義：有界な実数値関数/単関数　

　※関数定義関連ページ：1変数関数/2変数関数/ n変数関数/ベクトル値関数/写像一般　
　※実数値関数に関する諸概念の定義：実数値関数の極限/連続性/可測関数　　
　※総目次

定義：実数値関数　

定義

実数値関数とは、
「集合X（集合ならなんでもよい）の元に対して、実数を対応づける規則」
「集合Xの部分集合D（定義域）に属す各点にたいして、実数を対応づける規則」
「集合Xの部分集合D（定義域）から、実数体Rへの、写像」
のこと。
　　f : D→R　、f :X⊃D→R　　
などと表す。　　

[文献]
松坂『集合・位相入門』４章§4-B(pp.178-182);

定義

測度論などでは、
「集合X（集合ならなんでもよい）の元に対して、
　　　　　　　　　　　　広義の実数を対応づける規則」
「集合Xの部分集合D（定義域）に属す各点にたいして、
　　　　　　　　　　　　　　　広義の実数を対応づける規則」
「集合Xの部分集合D（定義域）から、広義の実数の集合R^*への、写像」
　　f : D→R^*　、f :X⊃D→R^*　　
という、「広義の実数値関数」とでもいえるものを定義して用いる。

[文献]
志賀『ルベーグ積分30講』17講(p.127)18講(p.134):図解つき;
伊藤『ルベーグ積分入門』§10(p.60);

下位
概念

・集合Xに実数体Rを指定したケース：単なる一変数関数「f :R⊃D→R」　
・集合XにR²を指定したケース：単なる2変数関数「f :R²⊃D→R」　
・集合XにRⁿを指定したケース：単なる n変数関数「f :Rⁿ⊃D→R」　

一般化

・ベクトル値関数/写像一般　

定義：実数値関数の定義域domain　

実数値関数「f :X⊃D→R」の定義域とは、
「Xの部分集合」Dのこと。

[具体例]1変数関数の定義域/ 2変数関数の定義域/ n変数関数の定義域
[一般化]ベクトル値関数の定義域

→[トピック一覧：実数値関数とその属性]
→総目次

定義：実数値関数の像・値　

点の像

「実数値関数f によるP∈Xの像」
「P∈Xにおけるf の値」
　　f (P)
とは、
f によってP∈Xに対応付けられた実数のこと。

[具体例]1変数関数の像･値/ 2変数関数の像･値/ n変数関数の像･値
[一般化]ベクトル値関数の像･値/写像の「像」

集合の像

「実数値関数f による『定義域の部分集合A』の像」f (A)とは、
『定義域の部分集合A』に属す元のfによる像を、全部集めて出来る集合のこと。
　つまり、f :X⊃D→R　、A⊂D⊂Xにたいして、f (A)={ f (a)∈R | a∈A⊂D⊂X }　と定義される。

定義：実数値関数の値域range　

実数値関数「f :X⊃D→R」のの値域とは、
f による定義域の像
　　 f (D)={ f (a)∈R | a∈D⊂X }
のこと。

[具体例]1変数関数の値域/ 2変数関数の値域/ n変数関数の値域
[一般化]ベクトル値関数の値域　

定義：実数値関数の逆像・原像inverse image　

点の逆像

「P∈D⊂Xが実数値関数『f :X⊃D→R』による実数bの逆像である」
　　P=f ⁻¹ (b)
とは、
P∈D⊂Xのf による像が実数bであるということ
　　　　f (P)=b
をいう。
※実数bのf による逆像は、複数存在しうる。

[具体例]
　1変数関数の逆像
　 2変数関数の逆像
　 n変数関数の逆像･原像
[一般化]
　ベクトル値関数の逆像　
　写像の「逆像」

[文献]黒田『微分積分学』3.1.2(p.86；87)

集合の
逆像

「実数値関数『f :X⊃D→R』による『R上の点集合B』の逆像」
　　f ⁻¹ (B)　
とは、
定義域Dに属す元のうち、その像がBに入るもの全体の集合のこと。
つまり、f :X⊃D→R　、B⊂Rにたいして、　　
　　　　　　f ^-1 (B)＝{ a∈D⊂X | f (a)∈B⊂R}　
と定義される。

定義：実数値関数の最大値・最大点・最小値・最小点　

最大値

「実数値関数f の集合Aにおける最大値」とは、
　　「f による『定義域の部分集合A』の像」の(実数の集合としての)最大元のこと。
つまり、　　　
f :X⊃D→R　、A⊂D⊂Xという設定のもとで、「実数値関数f の集合Aにおける最大値」といえば、max f (A)を指す。
※「実数値関数f の集合Aにおける最大値」は存在する場合もあれば、存在しない場合もある。
　　→最大値・最小値定理　　

[文献]

最大点

「P∈D⊂Xが、実数値関数f の集合Aにおける最大点である」とは、
「Pのf による像」f (P)が「f の集合Aにおける最大値である」ということ。
つまり、f :X⊃D→R , P∈A⊂D⊂Xとの設定下で「Pが実数値関数f の集合Aにおける最大点である」といえば、
　　　　　f (P)=max f (A)　となることを指す。　

最小値

「実数値関数f の集合Aにおける最小値」とは、
　　「f による『定義域の部分集合A』の像」の(実数の集合としての)最小元のこと。
つまり、f :X⊃D→R　、A⊂D⊂Xという設定のもとで、「実数値関数f の集合Aにおける最小値」といえば、
　　　　　min f (A)を指す。
※「実数値関数f の集合Aにおける最小値」は存在する場合もあれば、存在しない場合もある。
　　→最大値・最小値定理　　

最小点

「P∈D⊂Xが、実数値関数f の集合Aにおける最小点である」とは、
「Pのf による像」f (P)が、「f の集合Aにおける最小値である」ということ。
つまり、f :X⊃D→R, P∈A⊂D⊂Xとの設定下で「Pが 実数値関数fの集合Aにおける最小点である」といえば
　　　　　f (P)=min f (A)となることを指す。　

定義：実数値関数が有界　

有界

「実数値関数『f :X⊃D→R』が有界である」とは、
　 f の値域がR上の点集合として有界であるということ、
　つまり、
　「定義域Dに属すあらゆる元Pに対して、| f (P)|≦M」を満たす実数M>０が存在する
　　　　　論理記号では、（∃M>０）（∀P∈D⊂X）（| f (P) |≦M）　ということ
をいう。

[文献]
Rudin『現代解析学』4.13(p.87)距離空間一般上。
杉浦『解析入門I』I§6定義4(p.55);

点集合
で
有界

「実数値関数『f :X⊃D→R』が集合Aで有界である」とは、
　「f による『定義域の部分集合A』の像」f (A)がR上の点集合として有界であるということ。
　つまり、f :X⊃D→R　、A⊂D⊂Xという設定のもと、
　「集合Aに属すあらゆる元Pに対して、| f (P)|≦M」を満たす実数M>０が存在するということ
　　　論理記号では、（∃M>０）（∀P∈A⊂D⊂X）（| f (P) |≦M）　　

定義：単関数　simple function 　　

設定

単関数は次のように設定された舞台上で定義される。
Step1：集合X (集合ならなんでもよい)を用意する。
Step2：集合Xの部分集合をとり、Eと名づける。つまり、E⊂X　
Step3：実数を全てあつめた集合(実数体)R、
　　　　　　　　　ないしは、広義の実数を全てあつめた集合R*
　　　　を用意する　　
Step4：集合Eから実数体Rへの実数値関数「 f：E→R 」
　　　　ないし、
　　　　集合Eから「広義の実数の集合R*」への関数「f：E→R*」
　　　　を用意。
　　　　つまり、
　　　　　fとは、Xの部分集合の各元ごとに、
　　　　　　それに対応する実数ないし広義の実数を一つずつ定めた写像（点関数）。
　　　　　　　　

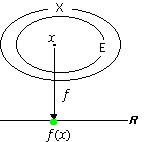
[文献]
伊藤『ルベーグ積分入門』§10(p.60);
志賀『ルベーグ積分30講』16講(p.122);18講(p.135);　
盛田『実解析と測度論の基礎』定義2.9(p.61);
志賀徳造『ルベーグ積分から確率論』p.34;
高橋『微分と積分2』§1.1定義1.1(p.2):R上の単関数
小谷『測度と積分』§2.2(p.24)

はじめに読むべき定義

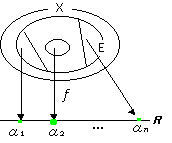
「実数値関数 f：E→R ないし 広義の実数値関数f：E→R^* が単関数である」とは、
　f のとる値が、有限nとおりの実数{α₁ ,α₂ ,α₃ ,…,α_n }に限られていて、
　　　α₁ のfによる逆像　f^−１( α₁ )={ x∈E| f(x)=α₁ }　　
　　　α₂ のfによる逆像　f^−１( α₂ )={ x∈E| f(x)=α₂ }　　
　　　α₃ のfによる逆像　f^−１( α₃ )={ x∈E| f(x)=α₃ }　　
　　　　　　：　　　　　　　　　　　　　　　
　　　α_n のfによる逆像　f^−１( α_n )={ x∈E| f(x)=α_n }　　
　が互いに素であって、
　f の定義域Eが、これらの直和 f^−１(α₁ )＋f^−１(α₂ )＋f^−１(α₃ )＋…＋f^−１(α_n )　となることをいう。　

きちんとした定義

「実数値関数 f：E→R ないし 広義の実数値関数f：E→R^* が単関数である」とは、
　定義域Eの直和分割{E₁,E₂,E₃,…,E_n}
　　　（つまり、　E＝E₁+E₂+E₃+…+E_nを満たす有限n個のの互いに素な集合E₁,E₂,E₃,…,E_n）
　　と、　
　　n個の相異なる実数α₁ , α₂ , α₃ , … , α_n　とがあって、
　　集合E_iの定義関数 χ_Ei ( )を用いて、
　　実数値関数 f：E→R ないし 広義の実数値関数f：E→R^* が　　
　　　　　f (x)=α₁χ_E1(x)+α₂χ_E2(x)+α₃χ_E3(x)+…＋α_nχ_En(x)　　
　　と表されること。
※したがって、
　　x∈E1ならば、 f(x)=α₁　、
　　x∈E2ならば、f(x)=α₂　、
　　x∈E3ならば、f(x)=α₃　、
　　：　
　　x∈E_nならば、f(x)=α_n　、
　となって、
　単関数f (x)は、有限nとおりの値しかとらない。

性質

・単関数が可測関数となるための必要十分条件　

下位
概念

・集合Xに実数体Rの部分集合を指定したケース