1変数関数の極限に関する諸定理　：　トピック一覧　


　・１変数関数の和差積商・定数倍と極限の順序交換　

　・コーシーの判定条件：普通の極限・右極限・左極限・一般化された極限/独立変数発散のときの極限　

　・単調関数と右極限・左極限

　・極限の存在条件と右極限・左極限　


※1変数関数の諸概念：
　1変数関数とその属性　/　極限の定義　/　無限小解析　/　連続性　/　微分　/　リーマン積分　
※極限関連ページ：
　数列の極限の性質
　2変数関数の極限の性質 / n変数関数の極限の性質 / n変数ベクトル値関数の極限の性質　
※総目次
 

1変数関数の和差積商・定数倍と極限の順序交換　






lim
 f(x)  ＝A 、　 lim
g(x)  ＝B  とすると、
x→x0
 		x→x0


【1. sum-difference limit theorem】


　　
　　　※なぜ？→証明

【2】


　　 　(c:定数)
　　　※なぜ？→証明 　




[文献]
　・吹田・新保『理工系の微分積分学』(p.20)
　・神谷浦井『経済学のための数学入門』(p.69) 




　　
　




【関数一般への拡張】


　→2変数関数の和差積商・定数倍と極限の順序交換　
　→n変数関数の和差積商・定数倍と極限の順序交換
　→ベクトル値関数のベクトル和と極限の順序交換/ベクトル値関数のスカラー倍と極限の順序交換　




【3. product limit theorem】


　　　
　　※なぜ？→証明

【4. quotient limit theorem】


　　　A≠0で、
　　　 　
　　　　※なぜ？→証明
　

定理：コーシーの判定条件 Cauchy Criterion for Limits of Function　[ x→ x0のとき] 


　x→x0のときf(x)が収束するための必要十分条件は、

　任意の（どんな）正の実数εに対して（でも）、
　その各々に応じて、ある正数δが存在し、
　　　　「　0＜|x−x0|＜δかつ0＜|x'−x0|＜δならば、　　|f(x)−f(x')|＜ε　」
　つまり「　x,x'∈ ( x0−δ, x0)∪( x0 , x0+δ)ならば、　　|f(x)−f(x') |＜ε　」
  を満たす、ということ、
  すなわち、
　∀ε>0　∃δ>0　（　x,y∈Uδ(a)∩(D−{a}) ⇒ |f(x)−f(y)|<ε　）　　
　　　　　　　　　(D: fの定義域、Uδ(a):aのδ近傍)　


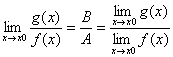
[文献]
　・吹田・新保『理工系の微分積分学』(p.20)
　・小平『解析入門I』78-9.;杉浦『解析入門』61-62;
　・住友『大学一年生の微積分学』124;
　・Fischer,Intermediate Real Analysis,238-239;
　・Lang, Undergraduate Analysis, 140-141 



※なぜ？→証明
 

【左極限・右極限等への拡張】 x→x0＋0のときの判定条件/x→x0−0のときの判定条件/一般化された条件
【関数一般への拡張】 2変数関数の場合のコーシー判定条件/n変数関数の場合のコーシー判定条件/ベクトル値関数の場合のコーシー判定条件    



→[トピック一覧：1変数関数の極限の性質]　　
→総目次　

定理：コーシーの判定条件　Cauchy Criterion for Limits of Function　[x→x0＋0のとき]


　　　[杉浦『解析入門I』p. 61→53は、片側極限も含む一般的な議論を展開]


　　　※広義積分の収束についてのコーシーの判定条件で使われているが、
　　　　これを明示したテキストが見当たらないので、
　　　　　1. x→x0のときの判定条件をベースに、自力でカスタマイズしつつ、
　　　　　2. 杉浦杉浦『解析入門I』p. 61→53の、より一般的な議論から特殊具体的を導く
　　　　ことによって、以下を作成した。よって要確認。
　以下の命題P,Qは同値である。
　命題P: x→x0＋0のときf(x)が収束する
　命題Q: 任意の正数εに対して、その各々に応じて、ある正数δが存在し、
　　　　　　　　　「0＜x−x0＜δかつ0＜x'−x0＜δならば、|f(x)−f(x')|＜ε」
　　　　　　つまり「x, x'∈( x0 , x0 +δ)ならば、|f(x)−f(x') |＜ε」
　　　　　を満たすということ、
　　すなわち、 ∀ε>0  ∃δ>0    ∀ x, x'  (x, x'∈( x0 , x0 +δ)⇒|f(x)−f(x') |＜ε)
※なぜ？→証明
  cf. x→ x0のときの判定条件/x→x0−0のときの判定条件/一般化された条件
※利用例→広義積分の収束についてのコーシーの判定条件　

→[トピック一覧：1変数関数の極限の性質]　　
→総目次　


定理：コーシーの判定条件Cauchy Criterion for Limits of Function　[ x→x0−0 のとき]


　　　[杉浦『解析入門I』p.61→53は、片側極限も含む一般的な議論を展開]

　※広義積分の収束についてのコーシーの判定条件で使われているが、
　　これを明示したテキストが見当たらないので、
　　　1. x→x0のときの判定条件をベースに、自力でカスタマイズしつつ、
　　　2. 杉浦『解析入門I』p.61→53の、より一般的な議論から特殊具体的を導く
　　ことによって、以下を作成した。よって要確認。
以下の命題P,Qは同値である。
命題P: x→x0−0のときf(x)が収束する
命題Q: 任意の正数εに対して、ある正数δが存在し、
　　　　　　　　　「−δ＜x−x0＜0かつ−δ＜x'−x0＜0ならば、|f(x)−f(x')|＜ε」
　　　　　　つまり「x, x'∈( x0−δ, x0 )ならば、|f(x)−f(x')|＜ε」
　　　　を成り立たせる、ということ、
　　すなわち、(∀ε>0)(∃δ>0) (∀ x, x') (x, x'∈( x0−δ, x0 )⇒ |f(x)−f(x')|＜ε)
※なぜ？→証明
cf. x→x0のときの判定条件/ x→x0＋0のときの判定条件/一般化された条件
※利用例→広義積分の収束についてのコーシーの判定条件　

→[トピック一覧：1変数関数の極限の性質]　　
→総目次　

定理:コーシーの判定条件 Cauchy Criterion for Limits of Function[x→x0/x0＋0/−0の判定条件の一般化]


　　　[『解析入門I』p. 61-2→53]
 
設定:以下で登場するB, x0については、
　B：関数f(x)の定義域の部分集合　　　　（つまり、集合Bは定義域に含まれる何らかの区間及びその合併）
　x0：x0∈「Bの閉包」(B∪「Bの境界」)　（つまり、x0はBで表される区間の内部か境界にある）
　　としておく。この設定が成り立たない場合、以下は、定義されないことになる。
本題:以下の命題P,Qは同値である。
命題P: 　xがB内でx0に近づくとき、f(x)が収束する。すなわち　f(x)→A (x→x0 , x∈B)　　
命題Q: 任意の正数εに対して、
　　　　　　「 x, x'∈Bかつ|x−x0|＜δかつ|x'−x0|＜δならば、|f(x)−f(x') |＜ε」
　　　つまり「x, x'∈B∩( x0−δ, x0+δ)ならば、|f(x)−f(x') |＜ε」
　　を成り立たせる、ある正数δが存在するということ、
　　すなわち、(∀ε>0)(∃δ>0) (∀ x, x') (x, x'∈B∩( x0−δ, x0+δ)⇒|f(x)−f(x') |＜ε)
※以上の議論は、
　B= (fの定義域)∩{ x |x≠x0}とすると、 x→ x0のときのコーシーの判定条件になり、
　　　∵B= {x|x≠x0}なら「x,x'∈B∩( x0−δ, x0+δ)ならば」を
　　　　　　　　　「x, x'∈( x0−δ, x0)∪( x0 , x0+δ)ならば」と言い換えても同じ。
　B= (fの定義域)∩{ x |x＞x0}とすると、 x→ x0+0のときのコーシーの判定条件になり、
　　　∵B= { x |x＞x0}なら「x,x'∈B∩( x0−δ, x0+δ)ならば」を「x, x'∈( x0 , x0+δ)ならば」と言い換えても同じ。
　B= (fの定義域)∩{ x |x＜x0}とすると、 x→ x0−0のときのコーシーの判定条件になる。
　　　∵B= { x |x＜x0}なら「x,x'∈B∩( x0−δ, x0+δ)ならば」を「x, x'∈( x0−δ, x0)ならば」と言い換えても同じ。

　※なぜ？→証明

　cf. x→x0のときの判定条件 / x→x0＋0のときの判定条件/x→x0−0のときの判定条件


→[トピック一覧：1変数関数の極限の性質]　　
→総目次　

定理：コーシーの判定条件　[ x→∞のとき]　


　[吹田新保『理工系の微分積分学』23.]　


　x→∞のときf(x)が収束するための必要十分条件は、
　任意の正数εに対して、
　　　　　「　x,x'＞K　ならば、　|f(x)−f(x')|＜ε　」
　を成り立たせるある数Kが存在するということ。
　　　すなわち、(∀ε>0)(∃K >0) (∀ x, x') ( x,x'＞K⇒|f(x)−f(x') |＜ε)
　これは、以下のように言い換えることもできる。
　　x→∞のときf(x)が収束するための条件は、
　　　　任意のの正数εに対して、
　　　　ある数Kをとると
　　　　　x＞K, h＞0　ならば　| f(x＋h)−f(x) |＜ε　
　　　　が成り立つことである。

　※証明：　x→x0のときのコーシーの判定条件の証明をベースに、自分で書いたもの。要確認。
　※利用例→広義積分の収束についてのコーシーの判定条件、　
　　
　　

　
→[トピック一覧：1変数関数の極限の性質]　　
→総目次　


単調関数と右極限・左極限

定理：fが開区間(a,b)で単調のとき、aでの右極限、bでの左極限が、ともに存在する。
　[吹田新保『理工系の微分積分学』21]

定理：fが開区間 (a,b)で狭義増加のとき、a＜c＜bなるcにつき
　　
　　　[吹田新保『理工系の微分積分学』22]


→[トピック一覧：1変数関数の極限の性質]　　
→総目次　

　


定理：

極限が存在するための条件は、右極限・左極限がともに存在して一致することである。　[吹田・新保『理工系の微分積分学』22.]


　
→[トピック一覧：1変数関数の極限の性質]　　
→総目次　

　

（reference）

『岩波数学辞典（第三版）』.項目166(pp436).
吉田耕作・栗田稔・戸田宏『平成元年3/31文部省検定済高等学校数学科用　高等学校　微分・積分　新訂版』啓林館、pp.28-33.
小平邦彦『解析入門I (軽装版) 』岩波書店、2003年、pp.78-9。
吹田・新保『理工系の微分積分学』学術図書出版社、1987年、pp.20-23.
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、p.95.
和達三樹『理工系の数学入門コース1・微分積分』岩波書店、1988年、pp.27-28.
杉浦光夫『解析入門』東京大学出版会、1980年、pp.57-63.
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.32-36;42-44.
住友洸『大学一年生の微積分学』現代数学社、1987年、p.124。
Chiang, Fundamental Methods of Mathematical Economics: Third Edition, McGraw Hill,1984. pp.145-147.
Fischer,Emanuel.Intermediate Real Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Heidelberg Berlin,1983,pp. 228-231; 238-239.
Lang,Serge.Undergraduate Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1983,pp.135-143.