|
|
|
定義: 2変数関数の点x0で微分可能differentiable・点x0における微分係数・導値differential coefficient |
|
図解
|

[java script1.1を使用]
|
|
|
|
直感的な
定義
|
[直感的な定義]
「z=f (x,y )は点 (x0,y0)で微分可能・全微分可能」とは、
z=f (x,y )が表す曲面{(x, y, z ) | z=f (x,y ) }に点(x0,y0, f (x0,y0 ))で接する平面
{(x, y, z ) | z= A (x-x0 )+ B (y-y0 ) +f ( x0,y0 ) }
を定められることをいい、
この接平面の法線ベクトル(A,B,1)の
第1・第2成分からなる2次元数ベクトル(A,B)を、
「点 (x0,y0)におけるf (x,y )の導値・微分係数」と呼ぶ。
つまり、
「点 (x0,y0)におけるf (x,y )の導値・微分係数」とは、
・z=f (x,y )が表す曲面に点(x0,y0, f (x0,y0 ))で接する平面のx軸方向への傾き
と
・z=f (x,y )が表す曲面に点(x0,y0, f (x0,y0 ))で接する平面のy軸方向への傾き
との組
のことである。
※微分係数(A,B)は勾配ベクトルに等しくなる[→定理]
※z= A (x-x0 )+ B (y-y0 ) +f ( x0,y0 )で表せない接平面も存在しうる。
それは、どういうときかというと…。
点 (x0,y0)で接するあらゆる平面は、
{(x, y, z ) | r(x- x0)+s(y- y0)+t (z- f ( x0,y0 ))=0}
で表せる。
t≠0ならば、
平面の方程式r(x- x0)+s(y- y0)+t (z- f ( x0,y0 ))=0について、
両辺をtで割って
(r/t) (x- x0)+(s/t) (y- y0)+ z- f ( x0,y0 )=0
移項して、
z =-(r/t) (x- x0)-(s/t) (y- y0)+f ( x0,y0 )
とできるので、
この平面を、z= A (x-x0 )+ B (y-y0 ) +f ( x0,y0 )のかたちで表せ、
この平面の法線ベクトルを(A,B,1)かたちで表せる。
ところが、
t=0ならば、
平面の方程式r(x- x0)+s(y- y0)+t (z- f ( x0,y0 ))=0は、
r(x- x0)+s(y- y0) =0
となってしまい、zが消去されてしまうので、
z= A (x-x0 )+ B (y-y0 ) +f ( x0,y0 )のかたちに変形しようがない。 |
[文献-数学]
・高木『解析概論』p. 55 ;
・吹田新保『理工系の微分積分学』6章§3Ⅱ(p.164) :2変数関数;
・小形『多変数の微分積分』pp. 46-50:2変数関数。ここでの説明とは別の説明。
・志賀『解析入門30講』25講(pp.193-5) :2変数関数;
・高橋『微分と積分2』§3.2 (p.71): 2変数関数;
・笠原『微分積分学』定義2.1(p.38);命題2.2(p.39)定義5.1(p.153):2変数関数
・杉浦『解析入門』Ⅱ§5定義1 (p.120):n変数実関数;
・杉浦『解析演習』Ⅱ章§2-2.2(p. 88-9) :n変数実関数
・『岩波数学辞典』333G全微分(p.985);
・黒田『微分積分学』8.3.2定義8.9(pp.285) :n変数実関数.
・Lang,Undergraduate Analysis,15-§2(pp.321-2);
・ルディン『現代解析学』9.10(p.207) :n変数ベクトル値関数.
・清野「多変数関数の微分」第5回(東京大学07 年度全学自由研究ゼミナール)
[文献-数理経済学]
・岡田『経済学・経営学のための数学』1.6(p.44):2変数関数
・de la Fuente, Mathematical Methods and Models for Economists, PartI-4-3 (p.170) :n変数ベクトル値関数.
・入谷久我『数理経済学入門』定義5.10(p.131) :n変数実関数.
・原・梶井『経済学のための数学』1.3.3全微分(p.10). |
|
| |
このように、
法線ベクトルの第三成分が0となる接平面(z軸に平行な接平面)は、
z= A (x-x0 )+ B (y-y0 ) +f ( x0,y0 )で表せない。
ここでは、このような接平面を接平面から除外して、
z= A (x- x0 )+ B (y-y0 ) +f ( x0,y0 )で表せる接平面のみを接平面と呼び、
z= A (x- x0 )+ B (y-y0 ) +f ( x0,y0 )で表せる接平面が定まることを、
微分可能と呼ぶ。
[→杉浦『解析入門』例12 (p.86)] |
[ 一般化]
・2変数関数の(全)微分可能
・多変数関数の(全)微分可能
・ベクトル値関数の(全)微分可能
|
|
厳密な
定義
|
「
z=f (x,y )は点P0=(x0,y0)で(全)微分可能で、点P0=(x0,y0)における微分係数は(A, B)である」
ということの定義は、
厳密には、次の数式で与えられる。
※ 表現1・表現2・表現3・表現4 はどれも同じ。
※ これらの定義は、1変数関数の微分定義2を、2変数関数へ拡張したもの。 |
|
|
[ 表現1a-ベクトル演算・増分を用いずに] |
|
「 z=f (x,y )は点(x0,y0)で(全)微分可能で、点(x0,y0)における微分係数は(A, B)である」とは、
「定点(x0,y0)に対して、ある一定の実数A,Bが存在して、
どの方向からであれ、いかなる経路を通ってであれ、定点(x0,y0)へ近づく動点(x,y)は、
{ f ( x,y )-(A(x-x0) + B (y-y0 ) + f ( x0,y0 ) )}/d ( (x,y), (x0,y0) ) →0 ( (x,y)→(x0,y0) )
を満たす」
ということ。
ランダウの記号を用いて表すと、
「点(x0,y0)に対して、ある一定の実数A,Bが存在して、
どの方向からであれ、いかなる経路を通ってであれ、定点(x0,y0)へ近づく動点(x,y)は、
f ( x,y )-( A(x-x0) + B (y-y0 ) + f ( x0,y0 ) )=o ( d ( (x,y), (x0,y0) ) ) ( (x,y)→(x0,y0) )
を満たす」
となる。
* d ( (x,y), (x0,y0) ) は、
点(x,y)から点(x0,y0)へのユークリッド距離{ (x-x0)2+(y-y0)2}1/2
を表す。 |
[文献]
笠原『微分積分学』定義5.1(p.153);
高橋『微分と積分2』§3.2 (p.71)
※微分係数(A,B)は勾配ベクトルに等しくなる[→定理] |
|
* この微分可能の定義は、
点( x0 , y0 )に対して、ある一定の実数A,Bが存在して、
「点(x,y)を点(x0,y0)に近づけたときの、
点(x,y)における《点(x0, y0, f ( x0,y0 ) )を通って、(A,B,1)を法線ベクトルとする平面A(x-x0) + B (y-y0 ) + f ( x0,y0 )》と《y= f ( x,y )》との誤差
f ( x,y )-(A(x-x0) + B (y-y0 ) + f ( x0,y0 ) )
が0に近づくスピードは、
d ( (x,y), (x0,y0) ) が0に近づくスピードよりも、速くなる」
ということを意味し、
ランダウの記号を用いて表すと、
「点(x0,y0)に対して、ある一定の実数A,Bが存在して、
f ( x,y )-( A(x-x0) + B (y-y0 ) + f ( x0,y0 ) )=o ( d ( (x,y), (x0,y0) ) ) ( (x,y)→(x0,y0) )
を満たす」
と表せる。 |
|
[ 表現1 b-ベクトル演算を用いずに・増分を用いて] |
|
「
z=f (x,y )は点(x0,y0)で(全)微分可能で、点(x0,y0)における微分係数は(A, B)である」とは、
「点(x0,y0)に対して、ある一定の実数A,Bが存在して、
どの方向からであれ、いかなる経路を通ってであれ、定点(x0,y0)へ近づく動点(x0+Δx, y0+Δy)は、
{ f ( x0+Δx, y0+Δy )-(AΔx + BΔy + f ( x0,y0 ) )}/ ∥(Δx,Δy)∥ →0 ( (Δx,Δy) →(0,0) )
を満たす」
ということ。
* ∥(Δx,Δy)∥ は、(Δx,Δy)のユークリッドノルム{ (Δx)2+(Δy)2}1/2 を表す。
これは、点(x0+Δx, y0+Δy)から点(x0,y0)へのユークリッド距離
d ( (x0+Δx, y0+Δy), (x0,y0) ) ={ (x0+Δx-x0)2+(y0+Δy-y0)2}1/2
に等しい。 |
[文献]
入谷久我『数理経済学入門』定義5.10(p.131) :n変数実関数.
※微分係数(A,B)は勾配ベクトルに等しくなる[→定理] |
|
* この微分可能の定義は、
点( x0 , y0 )に対して、ある一定の実数A,Bが存在して、
「『点(x0,y0)からの増分』(Δx,Δy)を(0,0)に近づけたときの、
点(x0+Δx, y0+Δy)における《点(x0, y0, f ( x0,y0 ) )を通って、(A,B,1)を法線ベクトルとする平面A(x-x0) + B (y-y0 ) + f ( x0,y0 )》と《y= f ( x,y )》との誤差
f ( x0+Δx, y0+Δy )-(A(x0+Δx-x0) + B (y0+Δy-y0 ) + f ( x0,y0 ) )=f ( x0+Δx, y0+Δy )-(AΔx + BΔy + f ( x0,y0 ) )
が0に近づくスピードは、
∥(Δx,Δy)∥ が0に近づくスピードよりも、速くなる」
ということを意味し、
ランダウの記号を用いて表すと、
「点(x0,y0)に対して、ある一定の実数A,Bが存在して、
f ( x0+Δx, y0+Δy )-( AΔx + BΔy + f ( x0,y0 ) )=o ( ∥(Δx,Δy)∥ ) ( (Δx,Δy) →(0,0) )
を満たす」
と表せる。
|
|
[ 表現1 c-ベクトル演算を用いて] |
|
|
「
z=f (x)は実2次元数ベクトルx 0で(全)微分可能で、x0における微分係数はaである」とは、
「x0に対して、ある一定の実2次元数ベクトルaが存在して、
どの方向からであれ、いかなる経路を通ってであれ、定点x0近づく動点x0+hは、
{ f ( x0+h )-(a・h + f (x0) )}/∥h∥ →0 (h→0 )
を満たす」
ということ。
あるいは、
「z=f (x)は実2次元縦ベクトルx 0で(全)微分可能で、x0における微分係数は実2次元横ベクトルaである」とは、
「実2次元縦ベクトルx0に対して、ある一定の実2次元横ベクトルaが存在して、
実2次元縦ベクトルhを、h→0 とすると、
{ f ( x0+h )-(ah+ f (x0) )}/∥h∥ →0
が満たされる」
ということ。
* a・hは、aとhとの内積を表す。
ahは、実2次元横ベクトルaと実2次元縦ベクトルhとの行列積を表す。
(どちらも、結果は同じとなる)
+は、実2次元数ベクトル空間に定められているベクトル和を表す。
-は、実数体に定義されている引き算を表す。
0は2次元零ベクトルを表し、0は実数の0を表す。
* ∥h∥ は、hのユークリッドノルムを表す。
これは、x0+hからx0へのユークリッド距離
d ( x0+h, x0 ) =∥(x0+h)-x0∥
に等しい。
* この微分可能の定義は、前述の表現1bを、以下の要領でベクトルを使って表現しなおしたもの。
・点(x0,y0) → 実2次元縦ベクトルx 0
・実数A,B → 実2次元横ベクトルa
・増分(Δx,Δy) → 実2次元縦ベクトルh
・点(x0+Δx, y0+Δy) → 実2次元縦ベクトルx0+h
・AΔx + BΔy → 内積a・h または、行列積ah
だから、この定義が意味するところは、表現1bとなんら変わらない。
|
[文献]
杉浦『解析入門』Ⅱ§5 定義1(5.4)(p.120)
|
|
|
[ 表現3b-ベクトル演算を用いずに、増分を用いて] |
|
|
「
z=f (x,y )は点P=(x0,y0)で(全)微分可能で、点P=(x0,y0)における微分係数は(A, B)である」とは、
「点(x0,y0)に対して、ある一定の実数A,Bが存在して、
どの方向からであれ、いかなる経路を通ってであれ、定点(x0,y0)に近づく動点(x0+Δx , y0+Δy)は、
Δz=f ( x0+Δx , y0+Δy )-f ( x0, y0 )=AΔx+ BΔy + o ( ∥(Δx,Δy)∥ ) ( (Δx,Δy)→(0,0) )
を満たす」
ということ。
* これは、
「点(x0,y0)に対して、ある一定の実数A,Bが存在して、
『 xをx0から「無限小の増分Δx」だけ増やし、yをy0から「無限小の増分Δy」だけ増やしたときの、f (x,y )の値の増分
Δz=f ( x0+Δx , y0+Δy )-f ( x0, y0 )
を、
(「無限小の増分Δx」の実数A倍)+(「無限小の増分Δy」の実数B倍)+(「無限小の増分(Δx,Δy)のノルム」より高次の無限小)
として表せる』
ということ」
を意味する。
* ランダウの記号o ( ∥(Δx,Δy)∥ )は、
「Δx,Δyの関数」のうち、
(Δx,Δy)→(0,0)としたときに、
「∥(Δx,Δy)∥が0に近づくよりも速いスピードで0に近づく」
ものを表す。 |
[文献]
・『岩波数学辞典』333G全微分(p.985):n変数関数.
・志賀『解析入門30講』25講(pp.193-5) :2変数関数;
※微分係数(A,B)は勾配ベクトルに等しくなる[→定理]
|
|
[ 表現3c-ベクトル演算を用いて] |
|
|
「
z=f (x)は実2次元数ベクトルx 0で(全)微分可能で、x0における微分係数はaである」とは、
「x0に対して、ある一定の実2次元数ベクトルaが存在して、
どの方向からであれ、いかなる経路を通ってであれ、定点x0近づく動点x0+hは、
Δy=f ( x0+h )-f (x0)=a・h + o ( ∥h∥ ) ( h → 0 )
を満たす」
ということ。
あるいは、
「z=f (x)は実2次元縦ベクトルx 0で(全)微分可能で、x0における微分係数は実2次元横ベクトルaである」とは、
「実2次元縦ベクトルx0に対して、ある一定の実2次元横ベクトルaが存在して、
実2次元縦ベクトルhを、h→0 とすると、
f ( x0+h )-f (x0)=ah+ o ( ∥h∥ ) ( h → 0 )
が満たされる」
ということ。
* a・hは、aとhとの内積を表す。
ahは、実2次元横ベクトルaと実2次元縦ベクトルhとの行列積を表す。
(どちらも、結果は同じとなる)
+は、実2次元数ベクトル空間に定められているベクトル和を表す。
-は、実数体に定義されている引き算を表す。
0は2次元零ベクトルを表し、0は実数の0を表す。
* ∥h∥ は、hのユークリッドノルムを表す。
これは、x0+hからx0へのユークリッド距離
d ( x0+h, x0 ) =∥(x0+h)-x0∥
に等しい。
* この微分可能の定義は、前述の表現1bを、以下の要領でベクトルを使って表現しなおしたもの。
・点(x0,y0) → 実2次元縦ベクトルx 0
・実数A,B → 実2次元横ベクトルa
・増分(Δx,Δy) → 実2次元縦ベクトルh
・点(x0+Δx, y0+Δy) → 実2次元縦ベクトルx0+h
・AΔx + BΔy → 内積a・h または、行列積ah
だから、この定義が意味するところは、表現3bとなんら変わらない。
|
[文献]杉浦『解析入門』Ⅱ§5 定義1(5.4)(p.120)
※微分係数(A,B)は勾配ベクトルに等しくなる[→定理] |
|
|
|
|
|
[ 表現4a-ベクトル演算・増分を用いずに] |
|
|
|
「
z=f (x,y )は点(x0,y0)で(全)微分可能で、点(x0,y0)における微分係数は(A, B)である」とは、
点(x0,y0)に対して、ある一定の実数A,Bが存在して、
f ( x,y )=f ( x0,y0 )+A(x-x0) + B (y-y0 ) +ε(x,y ) d ( (x,y), (x0,y0) )
と書くとき、(x,y) → (x0,y0)のとき、ε(x,y )→(0,0) を満たす
ということ。
* 表現2aでランダウの記号を用いない表現の一例。
|
[ 文献]
小平『解析入門Ⅱ』§6.2-b(p.267);
※微分係数(A,B)は勾配ベクトルに等しくなる[→定理]
|
|
[ 表現4b-ベクトル演算を用いずに・増分を用いて] |
|
|
「
z=f (x,y )は点(x0,y0)で(全)微分可能で、点(x0,y0)における微分係数は(A, B)である」とは、
点(x0,y0)に対して、ある一定の実数A,Bが存在して、
Δz=f ( x0+Δx , y0+Δy )-f ( x0, y0 )=AΔx+ BΔy + ε(x,y ) ∥(Δx,Δy)∥
と書くとき、(Δx,Δy)→(0,0)のとき、ε(x,y )→(0,0) を満たす
ということ。
|
[文献]
高木『解析概論』p. 55 :2変数関数;
吹田新保『理工系の微分積分学』6章§3Ⅱ(p.164) :2変数関数;
※微分係数(A,B)は勾配ベクトルに等しくなる[→定理] |
|
|
|
|
定理: 2変数関数の点(x0, y0)での微分可能性と偏微分可能性、微分係数と偏微分係数 |
|
定理
|
1. z=f (x,y )が点(x0,y0)で(全)微分可能ならば、
z=f (x,y )は、点(x0,y0)で、xについてもyについても偏微分可能。
2. z=f (x,y )が点(x0,y0)で(全)微分可能ならば、
点(x0,y0)における微分係数は、
点(x0,y0)における勾配ベクトル
grad f (x0,y0)=(∂f (x0,y0)/∂x , ∂f (x0,y0)/∂x)
に等しい。
※ z=f (x,y )が、点(x0,y0)で、xについてもyについても偏微分可能だとしても、
z=f (x,y )が点(x0,y0)で(全)微分可能とは限らない。
|
[文献]
・Lang,Undergraduate Analysis, 15-§2Theorem2.1(pp.322-3):証明つき;
・志賀『解析入門30講』25講(pp.194-5) :2変数関数:証明つき;
・杉浦『解析入門』Ⅱ§5定理5.2 (p.121): n変数実関数。方向微分から導出。
・高橋『微分と積分2』§3.2 定理3.11(p.72): 2変数関数;
・高木『解析概論』p.56;小平『解析入門Ⅱ』p.267;
・吹田新保『理工系の微分積分学』p.164. |
|
証明 |
「z=f (x,y )は点(x0,y0) で(全)微分可能で、点(x0,y0) における微分係数は(A, B)である」とは、
「点(x0,y0)に対して、ある一定の実数A,Bが存在して、
どの方向からであれ、いかなる経路を通ってであれ、
定点(x0,y0)へ近づく動点(x0+Δx, y0+Δy)は、
{ f ( x0+Δx, y0+Δy )-(AΔx + BΔy + f ( x0,y0 ) )}/ ∥(Δx,Δy)∥ →0 ( (Δx,Δy) →(0,0) )
を満たす」
ということであった。
だから、「z=f (x,y )は点(x0,y0) で(全)微分可能で、点(x0,y0) における微分係数が(A, B)である」ならば、
(i)左右から直進して、定点(x0,y0)へ近づく動点
つまり、動点(x0+Δx, y0+Δy)にΔy=0という制限を加えて、
(x0+Δx, y0)と表される動点だけを考えた特殊ケースでも、
(ii)上下から直進して、定点(x0,y0)へ近づく動点
つまり、動点 (x0+Δx, y0+Δy) )にΔx=0という制限を加えて、
(x0, y0+Δy) と表される動点だけを考えた特殊ケースでも、
{ f ( x0+Δx, y0+Δy )-(AΔx + BΔy + f ( x0,y0 ) )}/ ∥(Δx,Δy)∥ →0 ( (Δx,Δy) →(0,0) )
が満たされる。
特殊ケース(i) (ii)のそれぞれにおいて、
{ f ( x0+Δx, y0+Δy )-(AΔx + BΔy + f ( x0,y0 ) )}/ ∥(Δx,Δy)∥ →0 ( (Δx,Δy) →(0,0) )
を具体的に展開してみよう。 |
[文献]
志賀『解析入門30講』25講(pp.194-5)。 |
|
(i)
左右から直進して、定点(x0,y0)へ近づく動点だけを考えた特殊ケース、
つまり、
動点(x0+Δx, y0+Δy)にΔy=0という制限を加えて(x0+Δx, y0)と表される動点だけ
を考えた特殊ケースでは、
{ f ( x0+Δx, y0+Δy )-(AΔx + BΔy + f ( x0,y0 ) )}/ ∥(Δx,Δy)∥ →0 ( (Δx,Δy) →(0,0) )
は、Δy=0だから、
{ f ( x0+Δx, y0 )-(AΔx + f ( x0,y0 ) )}/ ∥(Δx,0)∥ →0 ( (Δx, 0) →(0,0) ) …(1-1)
となる。
ユークリッドノルムの定義より、∥(Δx,0)∥=Δx だから、
(1)は、
{ f ( x0+Δx, y0 )-(AΔx + f ( x0,y0 ) )}/Δx →0 ( (Δx, 0) →(0,0) ) …(1-2)
となる。
ここで2変数関数の極限(Δx, 0) →(0,0) は、
実質的には1変数の極限操作Δx→0だけをしているにすぎないから、
2変数関数の極限をとる(2)は、
{ f ( x0+Δx, y0 )-(AΔx + f ( x0,y0 ) )}/Δx→0 (Δx→0) …(1-3)
という1変数関数の極限に還元される。
{ f ( x0+Δx, y0 )-(AΔx + f ( x0,y0 ) )}/Δx =( f ( x0+Δx, y0 )-f ( x0,y0 ) )/Δx-A
であるから、
(1-3)は、
( f ( x0+Δx, y0 )-f ( x0,y0 ) )/Δx-A →0 (Δx→0)
となり、
したがって、( f ( x0+Δx, y0 )-f ( x0,y0 ) )/Δx → A (Δx→0) …(1-4)
(1-4)は、
「f ( x, y ) は、点 ( x0 , y0 )で、xに関して偏微分可能であり、
点(x0 , y0 )におけるf ( x, y )の偏微分係数∂f (x0,y0)/∂xはAである」
ということの定義に他ならない。 |

|
|
(ii)
上下から直進して、定点(x0,y0)へ近づく動点だけを考えた特殊ケース、
つまり、
動点 (x0+Δx, y0+Δy) )にΔx=0という制限を加えて、(x0, y0+Δy) と表される動点だけ
を考えた特殊ケースでは、
{ f ( x0+Δx, y0+Δy )-(AΔx + BΔy + f ( x0,y0 ) )}/ ∥(Δx,Δy)∥ →0 ( (Δx,Δy) →(0,0) )
は、Δx=0だから、
{ f ( x0, y0+Δy )-(BΔy + f ( x0,y0 ) )}/ ∥(0,Δy)∥ →0 ( (0,Δy) →(0,0) ) …(2-1)
となる。
ユークリッドノルムの定義より、∥(0,Δy)∥=Δy だから、
(2-1)は、
{ f ( x0, y0+Δy )-(BΔy + f ( x0,y0 ) )}/Δy →0 ( (0,Δy) →(0,0) ) …(2-2)
となる。
ここで2変数関数の極限(0,Δy) →(0,0) は、
実質的には1変数の極限操作Δy→0だけをしているにすぎないから、
2変数関数の極限をとる(2-2)は、
{ f ( x0, y0+Δy )-(BΔy + f ( x0,y0 ) )}/Δy →0 (Δy→0) …(2-3)
という1変数関数の極限に還元される。
{ f ( x0, y0+Δy )-(BΔy + f ( x0,y0 ) )}/Δy =( f ( x0, y0+Δy )-f ( x0,y0 ) )/Δy-B
であるから、
(2-3)は、
( f ( x0, y0+Δy )-f ( x0,y0 ) )/Δy-B →0 (Δy→0)
となり、
したがって、( f ( x0, y0+Δy )-f ( x0,y0 ) )/Δy → B (Δy→0) …(2-4)
(2-4)は、
「f ( x, y ) は、点 ( x0 , y0 )で、yに関して偏微分可能であり、
点(x0 , y0 )におけるf ( x, y )の偏微分係数∂f (x0,y0)/∂yはBである」 |
|
|
以上から、
「
z=f (x,y )は点(x0,y0) で(全)微分可能で、点(x0,y0) における微分係数が(A, B)である」ならば、
(i)左右から直進して、定点(x0,y0)へ動点(x,y)を近づけたケースから、
「f ( x, y ) は、点 ( x0 , y0 )で、xに関して偏微分可能であり、
点(x0 , y0 )におけるf ( x, y )の偏微分係数∂f (x0,y0)/∂xはAである」
ことが明らかになり、
(ii)上下から直進して、定点(x0,y0)へ動点(x,y)を近づけたケースから、
「f ( x, y ) は、点 ( x0 , y0 )で、yに関して偏微分可能であり、
点(x0 , y0 )におけるf ( x, y )の偏微分係数∂f (x0,y0)/∂yはBである」
ことが明らかになった。
つまり、
z=f (x,y )が点(x0,y0)で(全)微分可能ならば、
z=f (x,y )は、点(x0,y0)で、xについてもyについても偏微分可能であって、
点(x0,y0)における微分係数は、
点(x0,y0)における勾配ベクトル
grad f (x0,y0)=(∂f (x0,y0)/∂x , ∂f (x0,y0)/∂x)
に等しい。
|
|
|
※ |
z =f (x,y )が、点(x0,y0)で、xについてもyについても偏微分可能だとしても、
z=f (x,y )が点(x0,y0)で(全)微分可能とは限らない。
z=f (x,y )が、点(x0,y0)で、xについてもyについても偏微分可能なのに、(全)微分可能でない例をあげる。 |
|
例 1:次の関数は、点(0,0)において、x,yについて偏微分可能なのに、(全)微分可能でない。
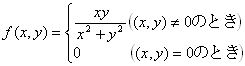 |
→吹田新保『 理工系の微分積分学』6章§3Ⅱ(p.164)
Lang,Undergraduate Analysis, 15-§2Theorem2.1(p.323): |
|
例 2:次の関数は、点(0,0)において、x,yについて偏微分可能なのに、(全)微分可能でない。
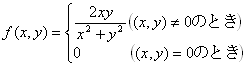 |
→杉浦『 解析入門』Ⅱ§5例3 (p.122) |
|
例 3:次の関数は、点(0,0)において、
x,yについて偏微分可能であるばかりか、あらゆる方向に方向微分可能なのに、
(全)微分可能でない。
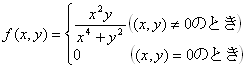 |
→杉浦『 解析入門』Ⅱ§5例4 (pp.122-3) |
|
例 4:次の関数は、点(0,0)において、x,yについて偏微分可能なのに、(全)微分可能でない。
f (x,y )=min{|x|,|y|}
|
→笠原『 微分積分学』5.1-例1(p.154):2変数関数
|
|
|
|
|
定理: 2変数関数に点(x0, y0)で接する接平面の方程式 |
|
定理
|
z=f (x,y )が点(x0,y0)で(全)微分可能ならば、
z=f (x,y )が表す曲面
{(x, y, z ) | z=f (x,y )}
に、
点( x0 , y0, f ( x0 , y0 ))で接する接平面の方程式は、
z=(∂f (x0,y0)/∂x ) (x-x0 )+(∂f (x0,y0)/∂y ) (y-y0 ) +f ( x0,y0 )
※解説
この方程式で表された平面が、たしかに、
曲面 z = f ( x , y )に点( x0 , y0, f ( x0 , y0 ))で接する接平面であることは、
以下の諸点より確かめられる。
1.接点( x0 , y0, f ( x0 , y0 ))を通っている。
2.曲面のx軸方向での傾きと、この平面のx軸方向での傾きは、ともに等しい。
※この平面をxで偏微分してみよ。
3.曲面のy軸方向での傾きと、この平面のy軸方向での傾きは、ともに等しい。
※この平面をyで偏微分してみよ。
4.この曲面とこの平面について、
xでの偏微分係数、yでの偏微分係数の両方が、等しければ、
θ方向微分係数の計算式より、
すべての方向θについて、方向微分係数(傾き)も等しくなる。 |
[文献]
・杉浦『解析入門』Ⅱ§5定義2 (p.120:n変数実関数。
・小形『多変数の微分積分』pp.55-61.
・志賀『解析入門30講』25講(pp.194-5) :2変数関数:証明つき
・高橋『微分と積分2』§3.2 定理3.11(p.72): 2変数関数;
|
|
証明 |
「
z=f (x,y )は点 (x0,y0)で微分可能・全微分可能」とは、
z=f (x,y )が表す曲面{(x, y, z ) | z=f (x,y ) }に点(x0,y0, f (x0,y0 ))で接する平面
{(x, y, z ) | z= A (x-x0 )+ B (y-y0 ) +f ( x0,y0 ) }
を定められることであった。
(全)微分可能ならば、微分係数(A,B)は勾配ベクトル
grad f (x0,y0)=(∂f (x0,y0)/∂x , ∂f (x0,y0)/∂x)
に等しくなるのだった[→定理]。
だから、A=∂f (x0,y0)/∂x , B=∂f (x0,y0)/∂x を、
{(x, y, z ) | z= A (x-x0 )+ B (y-y0 ) +f ( x0,y0 ) }
に代入すれば、接平面が得られたことになる。 |
|
|
|
|
定義: 2変数関数の全微分total differential |
|
|
z=f (x,y )が点(x0,y0)で(全)微分可能であるとき、
点( x0 , y0, f ( x0 , y0 ))でz=f (x,y )に接する接平面
z=g(x,y) = (∂f (x0,y0)/∂x ) (x-x0 )+(∂f (x0,y0)/∂y ) (y-y0 ) +f ( x0,y0 )
のうえで、
xについての増分Δx、yについての増分Δyにたいして、
z=g(x,y)がどれだけ増減するかを示す値
Δg= g(x+Δx,y+Δy)-g(x,y)
= (∂f (x0,y0)/∂x ) (x+Δx-x0 )+(∂f (x0,y0)/∂y ) (y+Δy-y0 ) +f ( x0,y0 )
-{ (∂f (x0,y0)/∂x ) (x-x0 )+(∂f (x0,y0)/∂y ) (y-y0 ) +f ( x0,y0 )}
= (∂f (x0,y0)/∂x ) Δx+(∂f (x0,y0)/∂y ) Δy
を「点(x0,y0)におけるf (x,y )の全微分」とよび、
d f ,
fx (x0,y0) dx+fy (x0,y0) dy
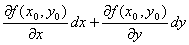
等で表す。
※このように、
「点(x0,y0)におけるf (x,y )の全微分」d fは、
接平面z=g(x,y)の増分Δg= g(x+Δx,y+Δy)-g(x,y)
なのであって、
z=f (x,y )そのものの増分Δf= f(x+Δx,y+Δy)-f(x,y)
とは別の概念であることに注意されたい。
|
[文献]
・笠原『微分積分学』定義5.2(p.154):2変数関数
・岡田『経済学・経営学のための数学』1.6(p.45)
・高橋『微分と積分2』§3.2 (p.71): 2変数関数;
[類概念]
. 1変数関数の微分differential,
|
|
※ |
z =f (x,y )が領域Dの各点で全微分可能であるとき、
点( x0, y0 )∈Dにおけるz=f (x,y)の全微分
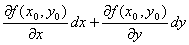
の値は、点( x0, y0 ) によって変わってくるから、領域D上の点( x0, y0 )の関数。
x0, y0をx,yと書き直した領域D上の関数
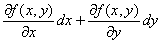
と書ける。 |
|
|
|
|
|
|
|