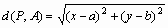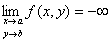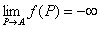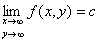2変数関数の極限・収束・発散の定義：トピック一覧　　

　　・定義：2変数関数、2変数関数の収束･極限値/累次極限/∞への発散/−∞への発散　　
　　・定理：2変数関数の極限と累次極限との関係/関数の収束と点列･数列の収束の関連性　

　※他のタイプの関数の極限の具体例：１変数関数の収束･極限値/ n変数関数の収束･極限値/実数値関数の極限/
　　　　　　　　　　　　　　　　　　　　ベクトル値関数の極限/距離空間のあいだの写像の極限　
　※2変数関数に関する諸概念の定義：2変数関数の諸属性/極限の性質/連続性/偏微分/全微分/矩形上の積分/点集合上の積分　
　→参考文献・総目次

定義：2変数関数　

定義

2変数関数とは、
「2個の実数の組(x,y)に対して、実数zを対応づける規則」
「2次元平面R²上の点集合（定義域）Dに属す各点Pにたいして、
　　　　　　　　　　　　　　　　　　　実数zを対応づける規則」
「2次元平面R²の部分集合Dから、実数体Rへの、写像」
のこと。
z=f (x,y)　、z=f (P)　、f : D→R　、f :R²⊃D→R　　などと表す。

→2変数関数の諸属性　

[文献]
西村『経済数学早分かり』3章§1.1関数とは(p.104)
小平
『解析入門�U』§6.1(p253);§6.4(p309);
笠原『微分積分学』1.4(pp.22-3)。
杉浦『解析入門I』I§6(p.50);
黒田『微分積分学』8.2.1(p.276);
��木『解析概論』8.函数(p.19)

定義の
ベクトル
表現

2個の実数の組(x,y)とは、実2次元数ベクトルのことにほかならないから、
2変数関数とは、
「実2次元数ベクトルx=(x,y)にたいして、実数zを対応づける規則」。
「実2次元数ベクトル空間R²の部分集合（定義域）Dの各元xに対して、
　　　　　　　　　　　　　　　　　　実数体Rの元zを対応づける規則」
「実2次元数ベクトル空間R²の部分集合から、実数体Rへの、写像」
などといっても同じ。
z=f (x)　、f: D→R　、f :R²⊃D→R　　などと表す。

関連

2変数関数の諸属性/極限の性質/連続性/偏微分/全微分/矩形上の積分/点集合上の積分　

定義：2変数関数の収束convergence・極限値limit　

→はじめに読むべき定義/ε-δ論法による定義/近傍概念による定義　

はじめに
読むべき
定義

「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が実数cに収束する」
「点P(x,y)を点A(a,b)に近づけたときの、関数f (x,y)の極限値は実数cである」
　　　f ( x,y )→c ( x→a , y→b )　f ( P )→c ( P → A )　　
　　　　　　　　　　　
　　　　　　　
とは、
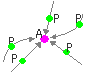
どの方向からであれ、いかなる経路を通ってであれ、
動点P(x,y)を、定点A(a,b)に一致させることなく定点A(a,b)に近づけると、
動点P(x,y)の定点A(a,b)への接近方向・接近経路にかかわらず、
関数f (x,y)の値が同じ１つの実数値cに近づくことをいう。
　　
※留意点　　
　　　(1)極限の定義において、点Pと点Aが一致することは除外している。　　
　　　　　点Aが関数f (x,y)の定義域に含まれているとは限らない。　
　　　(2) 点Pの点Aへの接近方向・接近経路によって、
　　　　　f (x,y)が近づく値が異なるときには、
　　　　　「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)がcに収束しない」
　　　　　「点P(x,y)を点A(a,b)に近づけたとき、
　　　　　　　　関数f (x,y)に極限値は存在しない」という。　
※この定義は一見わかりやすい。
　ところが、「近づく」とはいかなる事態を指すのか、という点が、
　明らかにされておらず、
　この「収束」「極限」定義は、実のところは不正確で、
　証明での使用に耐えられない。
　そこで、
　「近づく」の意味を明確化するために、
　「収束」「極限」概念は、次のように厳密に定義される。　

cf.2変数関数の累次極限　

[他のタイプの関数の極限]
・１変数関数の収束･極限値
・ n変数関数の収束･極限値
・実数値関数の極限
・ベクトル値関数の極限
・距離空間のあいだの写像の極限

[活用例]
・2変数関数の連続性の定義
・2変数関数の偏微分の定義

[文献]
和達『微分積分』pp.112-114;
矢野・田代『社会科学者のための基礎数学改訂版』p. 91. 　
高橋『経済学とファイナンスのための数学』pp.141-142.;
小平『解析入門�U』定義6.1(p.259);
黒田『微分積分学』定義8.6(p.277);
��木『解析概論』9極限(p.20).　

→「2変数関数の収束・極限の定義」先頭

厳密な
定義：
ε-δ
　論法

「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が実数cに収束する」
「点P(x,y)を点A(a,b)に近づけたときの、関数f (x,y)の極限値は実数cである」
　　　　f ( x,y )→c ( x→a , y→b )　f ( P )→c ( P → A )　　
　　　　　　　　　　　
　　　　　　　
とは、
任意の（どんな）正の実数εに対して（でも）、ある正の実数δをとると、
　　０＜d( P, A )＜δ ⇒ d ( f (P), c )＜ε　　　
が成り立つ
ということ。
この定義を、論理記号で表せば、
（∀ε>０）（∃δ>０）（∀P∈R² ）（０＜d( P, A )＜δ⇒d ( f (P), c )＜ε ）　
となる。
　　　　＊　d ( P, A )は、2次元平面R²上での点Pと点Aとの距離を、
　　　　　　d ( f (P), c )は、R上のf (P)とcとの距離| f (P)−c|を表す。　

[文献]
小平『解析入門�U』p.259;
笠原『微分積分学』1.4[2](p.28);
吹田新保『理工系の微分積分学』pp.158-159.
高橋『経済学とファイナンスのための数学』p. 143;
��木『解析概論』p.20.
ルディン『現代解析学』4.1(p.81):距離空間一般上。

※ユークリッド距離が定められたユークリッド空間R²における極限概念　　　　　
　2変数関数f (x,y)、すなわち、「2次元平面R²の部分集合から、実数体Rへの、写像」について、
　収束・極限を扱う際には、
　特別な目的がない限り、
　2次元平面R²上の距離をユークリッド距離で定めて、2次元平面R²をユークリッド平面R²とし、　
　実数体Rの距離をユークリッド距離で定めて、Rを1次元ユークリッド空間Rとする設定のもとで
　考えるのが普通。　
　この設定下では、
　　　　　　
　　　　d ( f (P), c )=| f (P)−c|=| f (x,y)−c|　　
　だから、
　「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が実数cに収束する」
　「点P(x,y)を点A(a,b)に近づけたときの、関数f (x,y)の極限値は実数cである」
　の定義は、具体的には
　　┌任意の（どんな）正の実数εに対して（でも）、
　　｜ある正の実数δが存在して、
　　｜　　　「　　
　　｜　　　　　　　　ならば 　| f (x,y)−c|＜ε　」　　
　　└を成り立たせる
　　（∀ε>０）（∃δ>０）（∀x,y∈R ）（⇒| f (x,y)−c|＜ε ）　
　となる。

※2次元数ベクトル空間の上に定義されたユークリッド空間R²における極限概念　　　　　
　R²にベクトルの加法･スカラー乗法･自然な内積(標準内積)･ユークリッドノルム‖‖が定義されており、
　R²を実2次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
　任意の実2次元数ベクトルx, y∈R²のユークリッド距離は‖x−y‖　と表せる。
　このユークリッド距離を定義したユークリッド平面R2のもとでは、　
　d( P, A )＝‖P−A‖　
　だから、
　「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が実数cに収束する」
　「点P(x,y)を点A(a,b)に近づけたときの、関数f (x,y)の極限値は実数cである」
　の定義は、
　　┌任意の（どんな）正の実数εに対して（でも）、
　　｜ある正の実数δが存在して、
　　｜　　　「　０＜‖P−A‖＜δ　ならば 　| f (P)−c|＜ε　」　
　　｜　　　　　　　　　　
　　└を成り立たせる
　　（∀ε>０）（∃δ>０）（∀P∈R² ）（０＜‖P−A‖＜δ⇒| f (P)−c|＜ε ）　
　と表せる。　　　
　ただし、上記のPは、「点P(x,y)」を表す実2次元数ベクトル(x,y)、
　　　　　上記のAは、「点A(a,b)」を表す実2次元数ベクトル(a,b)
　である。　　　

→「2変数関数の収束・極限の定義」先頭

近傍を
用いた
定義

「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が実数cに収束する」
「点P(x,y)を点A(a,b)に近づけたときの、関数f (x,y)の極限値は実数cである」
　　　　　　　　　　　
　　　　　　　
とは、
　実数cの任意の（どんな）「R上のε近傍U_ε(c)」に対して（でも）、
　ある「R²上の点Aの除外δ近傍U*_δ(A)」が存在して、
　　　　　f ( U*_δ(A) ) ⊂U_ε(c)　
　を満たす
ということ。
この定義を別の表現でいうと、
　任意の（どんな）正の実数εに対して（でも）、ある正の実数δが存在して、
　　　　　　　　「　f ( U*_δ(A) ) ⊂U_ε(c)　　」
　　　　すなわち「　(x,y)∈U*_δ(A) ならば、　f(x,y) ∈U_ε(c)」
　を成り立たせる、
ということ。
この定義を、論理記号で表せば、
（∀U_ε(c)）（∃U*_δ(A)）（ f ( U*_δ(A) ) ⊂U_ε(c) ）　
（∀ε>０）（∃δ>０）（ f ( U*_δ(A) ) ⊂U_ε(c) ）　
（∀ε>０）（∃δ>０）（∀P∈R² ）（ P∈U*_δ(A) ⇒ f (P) ∈U_ε(c)）　
となる。

[文献]
笠原『微分積分学』1.4[2](p.28);

※ユークリッド距離が定められたユークリッド空間R²における極限概念　　　　　
　2変数関数f (x,y)、すなわち、「2次元平面R²の部分集合から、実数体Rへの、写像」について、
　収束・極限を扱う際には、
　特別な目的がない限り、
　2次元平面R²上の距離をユークリッド距離で定めて、2次元平面R²をユークリッド平面R²とし、　
　実数体Rの距離をユークリッド距離で定めて、Rを1次元ユークリッド空間Rとする
　設定のもとで考えるのが普通。　
　この設定のもとでは、
　点A(a,b)の「R²上の除外δ近傍U*_δ(A)」は、
　　　　　　
　実数cの「R上のε近傍U_ε(c)」は、(c−ε,c＋ε)　
　だから、
　「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が実数cに収束する」
　「点P(x,y)を点A(a,b)に近づけたときの、関数f (x,y)の極限値は実数cである」
　の定義は、具体的には
　　┌任意の（どんな）正の実数εに対して（でも）、
　　｜ある正の実数δが存在して、
　　｜　　　　　　　
　　｜　　　　　　　　ならば 　f (P)∈(c−ε,c＋ε)　　　
　　└を成り立たせる
　となる。

※2次元数ベクトル空間の上に定義されたユークリッド空間R²における極限概念　
　R²にベクトルの加法･スカラー乗法･自然な内積(標準内積)･ユークリッドノルム‖‖が定義されており、
　R²を実2次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
　任意の実2次元数ベクトルx, y∈R²のユークリッド距離は‖x−y‖　と表せる。
　このユークリッド距離を定義したユークリッド平面R2のもとでは、　
　点A(a,b)の「R²上の除外δ近傍U*_δ(A)」は、U^*_δ(A)＝{ Q∈R² | ０＜‖Q−A‖＜ε }　
　実数cの「R上のε近傍U_ε(c)」は、(c−ε,c＋ε)　
　だから、
　「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が実数cに収束する」
　「点P(x,y)を点A(a,b)に近づけたときの、関数f (x,y)の極限値は実数cである」
　の定義は、
　　┌任意の（どんな）正の実数εに対して（でも）、
　　｜ある正の実数δが存在して、
　　｜　　　P∈U^*_δ(A)＝{ Q∈R² | ０＜‖Q−A‖＜ε }　
　　｜　　　ならば 　　
　　｜　　　f (P)∈(c−ε,c＋ε)　　
　　└を成り立たせる
　と表せる。　　　
　ただし、上記のPは、「点P(x,y)」を表す実2次元数ベクトル(x,y)、
　　　　　上記のAは、「点A(a,b)」を表す実2次元数ベクトル(a,b)
　である。　　　

→[トピック一覧：2変数関数の極限]
→総目次

定義：2変数関数の累次極限　

定義

2変数関数の極限に対して、
　　
　　
を累次極限とよぶ。

[文献]
吹田・新保『理工系の微分積分学』p. 159. .

定理：2変数関数の極限と累次極限　

定理

2変数関数の極限
　　　　
が存在するなら、
二つの累次極限　　
　　　
　　　
が存在して、ともにcに等しい。
　　（ただし、{　}内の極限は存在するものとする）　

[文献]
吹田・新保『理工系の微分積分学』p. 159.

例

以下の原点での極限は？
　　　　
　　原点での二つの累次極限は存在する。　
　　
　　　　　
　　しかし、このように、原点への近づけ方で値が変わるため、
　　同時にx→０,y→０としたときの極限　　
　　　　　
　　は存在しない。

→[トピック一覧：2変数関数の極限]
→総目次

定理：2変数関数の収束の、点列・数列の収束への言い換え　

定理1

次の命題P,Q,Rは互いに言い換え可能である。
つまり、命題P⇔命題Q⇔命題R。
命題P：
　点P(x,y)を点A(a,b)に近づけたとき、
　　　関数f ( P )=f (x,y)が実数cに収束する　
　これを記号で表すと、
　　　f ( P )→c ( P → A )　
　　　f (x,y)→c ( x→a , y→b )　
　　　　　
　　　　
　など。　

→ 1変数関数の収束の、数列の収束への言い換え
→ n変数関数の収束の、点列･数列の収束への言い換え
→実数値関数の収束の、点列・数列の収束への言い換え
→ベクトル値関数の収束の、点列の収束への言い換え
→距離空間の間の写像の収束の、点列の収束への言い換え

[文献]
吹田・新保『理工系の微分積分学』p. 159.
小平『解析入門�U』p.259:証明略;
杉浦『解析入門I』p.53:証明付;
��木『解析概論』9極限(p.22):証明付.
ルディン『現代解析学』4.1(p.81):距離空間一般上。

命題Q：
　どんなR²上の点列{ P_n }={ P₁ , P₂ , P₃,…}={ (x₁ ,y₁ ) , (x₂ ,y₂ ), (x₃ ,y₃ ),…}についてであれ、　
　　1. その点列{ P_n }={ P₁ , P₂ , P₃,…}={ (x₁ ,y₁ ) , (x₂ ,y₂ ), (x₃ ,y₃ ),…}が点A(a,b)に収束し、　
　　 かつ 　
　　2. その点列の各項 P₁ , P₂ , P₃,…がどれも点Aと一致しない　
　限り、　
　その点列の各項 P₁ , P₂ , P₃,…を２変数関数f によりR上に写した像の数列　
　　　　{ f ( P_n ) }={ f ( P₁ ), f ( P₂ ) , f ( P₃ ) ,… }={ f ( x₁ ,y₁ ) , f (x₂ ,y₂ ), f (x₃ ,y₃ ),… }
　は実数cに収束する。
　つまり、
　　任意のR²上の点列{ P_n }={ P₁ , P₂ , P₃,…}={ (x₁ ,y₁ ) , (x₂ ,y₂ ), (x₃ ,y₃ ),…}について、
　　　P_n→A (n→∞) かつ　P₁≠A , P₂≠A , P₃≠A ,…ならば、f (P_n)→c (n→∞)　　
　論理記号で表すと、
　　　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ f (P_n)→c (n→∞)）

命題R：いかなる「実数aに収束する数列{ x₁ , x₂ , x₃ ,…}」と
　　　　　　　　「実数bに収束する数列{ y₁ , y₂ , y₃ ,…}」に対しても、
　　　　（ただし、x₁≠a , x₂≠a , x₃≠a ,… 、y₁≠b , y₂≠b , y₃≠b ,… ）
　　　　数列
　　　　　　{ f ( P_n ) }={ f ( P₁ ) , f ( P₂ ), f ( P₃ ),…}={ f ( x₁ ,y₁ ) , f (x₂ ,y₂ ), f (x₃ ,y₃ ),…}
　　　　が実数cに収束する。
　　　　つまり、
　　　（∀ { x_n } { y_n } ）
　　　　　　（（(∀n) (x_n ≠a かつ y_n ≠b ) かつ x_n→a (n→∞) かつ y_n→b (n→∞)）⇒ f (x_n ,y_n)→c (n→∞)）
※なぜ？
　・「命題P⇒命題Q」となるわけ→証明　　
　・「命題Q⇒命題P」となるわけ→証明　　
　・「命題Q⇔命題R」となるのは、点列の収束と数列の収束の関係による。　

定理2

点P(x,y), 点A(a,b)とする。　　
P → A のとき、
f ( P )が収束するための必要十分条件は、
点A(a,b)に収束するどんな点列{ P_n }（ただし、P_n∈D, P_n ≠A ）に対しても、
数列 { f ( P_n ) }が収束することである。
　　　　※極限値の値をだしていないことに注意。

活用例

コーシーの判定条件　

定義：∞に発散する　

はじめに
読むべき
定義

「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が∞に発散する」　
　　　f ( x,y )→＋∞( x→a , y→b )　　　f ( P )→＋∞ ( P → A )　
　　　　　　　
とは、
点P(x,y)を、点A(a,b)に一致させることなく点A(a,b)に近づけるとき、　
関数f(x,y)が限りなく大きくなることをいう。
※この定義は一見わかりやすい。
　ところが、
　「近づく」「限りなく大きくなる」とはいかなる事態を指すのかという点が、
　明らかにされておらず、
　この「発散」定義は不正確で、証明のなかでは使いものにならない。
　そこで、
　「近づく」「限りなく大きくなる」の意味を明確化するために、
　「発散」概念は、次のように厳密化される。　

→1変数関数の発散

→ n変数関数の発散

[文献]
高木・押切
『解析Ｉ・微分』p.25.

厳密な
定義

「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が∞に発散する」　
　　　f ( x,y )→＋∞( x→a , y→b )　　　f ( P )→＋∞ ( P → A )　
　　　　　　　
とは、
任意の（どんな大きな）実数Kに対して(でも)、ある正の実数δをとると、
　　　「０＜d( P, A )＜δ ならば f (x,y)＞K　」　　　　
が成りたつ
ということ。
この定義を、論理記号で表せば、
（∀K∈R）（∃δ>０）（０＜d( P, A )＜δ⇒f (x,y)＞K ）　
となる。
　　＊　d ( P, A )は、2次元平面R²上での点Pと点Aとの距離を表す。　

杉浦
『解析入門I』I§6定義8(p.60);

Euclid平面
において

2変数関数f (x,y)、すなわち、「2次元平面R²の部分集合から、実数体Rへの、写像」について、
収束・極限・発散等を扱う際には、
特別な目的がない限り、
2次元平面R²上の距離をユークリッド距離で定めて、2次元平面R²をユークリッド平面R²とする
設定のもとで考えるのが普通。　
この設定下では、
　　　　　
だから、
「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が∞に発散する」　
の定義は、具体的には
　　┌任意の（どんな大きな）実数Kに対して（でも）、
　　｜ある正の実数δをとると、
　　｜　　　「　
　　｜　　　　　　　　ならば　f (x,y)>K　」　　
　　└を成り立たせる
　　（∀K∈R）（∃δ>０）（⇒ f (x,y) > K ）　
となる。

数ベクトル空間
の上に
定義された
Euclid平面
において

R²にベクトルの加法･スカラー乗法･自然な内積(標準内積)･ユークリッドノルム‖‖が定義されており、
R²を実2次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実2次元数ベクトルx, y∈R²のユークリッド距離は‖x−y‖　と表せる。
このユークリッド距離を定義したユークリッド平面R2のもとでは、　
　d( P, A )＝‖P−A‖　
だから、
「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が∞に発散する」の定義は、
　　┌任意の（どんな大きな）実数Kに対して（でも）、
　　｜ある正の実数δが存在して、
　　｜　　　「　０＜‖P−A‖＜δ　ならば 　f (x,y)>K　　」　
　　└を成り立たせる
　　（∀K∈R）（∃δ>０）（０＜‖P−A‖＜δ⇒f (x,y)>K ）　
　と表せる。　　　
　ただし、上記のPは、「点P(x,y)」を表す実2次元数ベクトル(x,y)、
　　　　　上記のAは、「点A(a,b)」を表す実2次元数ベクトル(a,b)
　である。　　　

定義：−∞に発散する　

はじめに
読むべき
定義

「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が−∞に発散する」　
　　f ( x,y )→−∞ ( x→a , y→b )　、　f ( P )→−∞ ( P → A )　
　　　　
とは、
点P(x,y)を、点A(a,b)に一致させることなく点A(a,b)に近づけるとき、　
関数f(x,y)が限りなく小さくなることをいう。
※この定義は一見わかりやすい。
　ところが、
　「近づく」「限りなく小さくなる」とはいかなる事態を指すのかという点が、
　明らかにされておらず、
　この「発散」定義は不正確で、証明のなかでは使いものにならない。
　そこで、
　「近づく」「限りなく小さくなる」の意味を明確化するために、
　「発散」概念は、次のように厳密化される。　

→1変数関数の発散
→ n変数関数の発散

[文献]
高木・押切
『解析Ｉ・微分』p.25.

厳密な
定義

「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が−∞に発散する」　
　　f ( x,y )→−∞ ( x→a , y→b )　、　f ( P )→−∞ ( P → A )　
　　　　
とは、
任意の（どんな小さな）実数Kに対して(でも)、ある正の実数δをとると、　　
　　　「０＜d( P, A )＜δ ならば f (x,y)<K　」　　　　
が成りたつ
ということ。
この定義を、論理記号で表せば、
（∀K∈R）（∃δ>０）（０＜d( P, A )＜δ⇒f (x,y)<K ）　
となる。
　　＊　d ( P, A )は、2次元平面R²上での点Pと点Aとの距離を表す。　

杉浦
『解析入門I』I§6定義8(p.60);

Euclid平面
において

2変数関数f (x,y)、すなわち、「2次元平面R²の部分集合から、実数体Rへの、写像」について、
収束・極限・発散等を扱う際には、
特別な目的がない限り、
2次元平面R²上の距離をユークリッド距離で定めて、2次元平面R²をユークリッド平面R²とする
設定のもとで考えるのが普通。　
この設定下では、
　　　
だから、
「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が−∞に発散する」　
の定義は、具体的には
　　┌任意の（どんな小さな）実数Kに対して（でも）、
　　｜ある正の実数δをとると、
　　｜　　　「　
　　｜　　　　　　　　ならば　f (x,y)<K　」　　
　　└を成り立たせる
　　（∀K∈R）（∃δ>０）（⇒ f (x,y) < K ）　
となる。

数ベクトル空間
の上に
定義された
Euclid平面
において

R²にベクトルの加法･スカラー乗法･自然な内積(標準内積)･ユークリッドノルム‖‖が定義されており、
R²を実2次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実2次元数ベクトルx, y∈R²のユークリッド距離は‖x−y‖　と表せる。
このユークリッド距離を定義したユークリッド平面R2のもとでは、　
　d( P, A )＝‖P−A‖　
だから、
「点P(x,y)を点A(a,b)に近づけたとき、関数f (x,y)が−∞に発散する」の定義は、
　　┌任意の（どんな小さな）実数Kに対して（でも）、
　　｜ある正の実数δが存在して、
　　｜　　　「　０＜‖P−A‖＜δ　ならば 　f (x,y)<K　　」　
　　└を成り立たせる
　　（∀K∈R）（∃δ>０）（０＜‖P−A‖＜δ⇒f (x,y)<K ）　
　と表せる。　　　
　ただし、上記のPは、「点P(x,y)」を表す実2次元数ベクトル(x,y)、
　　　　　上記のAは、「点A(a,b)」を表す実2次元数ベクトル(a,b)
　である。