n次元ユークリッド空間 : トピック一覧
・自然な内積:自然な内積の定義、自然な内積の性質、自然な内積と内積・計量実ベクトル空間一般
・ユークリッドノルム:ユークリッドノルムの定義、ノルム・ノルム空間一般との関係
・ユークリッド距離:ユークリッドノルムから定められる距離の定義、ユークリッド距離との関係、実n次元数ベクトル空間からユークリッド空間
・ユ―クリッド空間における基本概念:直交、角、単位ベクトル、単位ベクトル化
※計量実ベクトル空間Rn関連ページ:ノルム・ノルム空間の定義/内積・計量実ベクトル空間の定義
※ユークリッド空間Rn関連ページ:内積の性質/正規直交系・正規直交基底の定義/直交系・直交基底と内積/直交系・正規直交系の性質/正規直交基底の存在と構成/計量同型写像
※ユークリッド空間Rnの部分空間関連ページ:ユークリッド空間の部分空間の基底/直交補空間/部分空間の直交/ユークリッド空間の部分空間の正規直交基底の存在/直交射影
定義:実n次元数ベクトル空間における(自然な)内積・標準内積
【舞台設定】
R:実数体
Rn:実n次元数ベクトル空間
x, y:実n次元数ベクトル。具体的に書くと、x1, x2, …, xn∈Rとして、x=( x1, x2, …, xn )∈Rn 、 y1, y2, …, yn∈Rとして、y=( y1, y2, …, yn )∈Rn
【本題】
実n次元数ベクトル空間Rnにおいて、実n次元数ベクトルx=( x1, x2, …, xn ), y=( y1, y2, …, yn )の(自然な)内積 x・y は、
x・y=x1y1+x2y2+…+xnyn 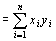
と定義される。
※実n次元数ベクトルx,yの(自然な)内積 x・y は、実数。
※実n次元数ベクトルx,yが横ベクトルのとき、行列の積を用いて、 x・y=xty=( x1, x2, …, xn)t( y1, y2, …, yn )
実n次元数ベクトルx,yが縦ベクトルのとき、行列の積を用いて、x・y=txy とも表せる。
※内積によって定義される概念:内積により定まるノルム、ベクトルの直交、ベクトルのなす角
※自然な内積は内積の一例、自然な内積の性質
※(自然な)内積以外の内積〈 x,y 〉の例については、ホフマン・クンツェ『線形代数学II』8.1例1(p.92)を参照。
【文献】
砂田『行列と行列式』例7.5(p.239);神谷浦井『経済学のための数学入門』§3.2.3(p.124);志賀『ベクトル解析30講』第11講(pp.80-81):なぜ数ベクトル空間でこのような内積が使われるのかまで説明; 斎藤『線形代数入門』2章§6(p.61);4章§6例1(p.120);永田『理系のための線形代数の基礎』4.1(p.113-4);佐武『線形代数学』Ⅰ§6(p.31);ホフマン『線形代数学II』8.1例1(p.92);草場『線形代数』定義5.2(p.128);
杉浦『解析入門I』I§4定義2(p.36);西村『経済数学早わかり』2章§1.4(p.33);布川『線形代数と凸解析』例4.1(p.64);柳井竹内『射影行列・一般逆行列・特異値分解』§1.1.1(p.1;4);佐和『回帰分析』2.1.4内積と射影(p.21)
定理:自然な内積の性質
【舞台設定】
R:実数体
Rn:実n次元数ベクトル空間
x, y:実n次元数ベクトル
具体的に書くと、x1, x2, …, xn∈Rとして、x=( x1, x2, …, xn )∈Rn 、 y1, y2, …, yn∈Rとして、y=( y1, y2, …, yn )∈Rn
【本題】
実n次元数ベクトル空間 Rn における 実n次元数ベクトルx=( x1, x2, …, xn ) , y=( y1, y2, …, yn ) の(自然な)内積x・yは、次に示す4つの性質を満たす。
※活用例:自然な内積と、内積・計量実ベクトル空間
[性質1:線形性1]
任意の実n次元数ベクトルx1,x2,y∈Rnにたいして、(x1+x2)・y=x1・y+x2・y
任意の実n次元数ベクトルx,y1,y2∈Rnにたいして、x・( y1+y2 ) =x・y1+x・y2
すなわち、∀x1,x2,y∈Rn ( (x1+x2)・y=x1・y+x2・y )、 (∀x,y1,y2∈Rn) ( x・( y1+y2 ) =x・y1+x・y2 )
※なぜ?→証明
[性質2:線形性2]
任意の実n次元数ベクトルx,y∈Rnと任意の実数aにたいして、(ax)・y=a (x・y), x・(ay)=a (x・y)
すなわち、∀x,y∈Rn ∀a∈R ( (ax)・y=a (x・y) かつ x・(ay)=a (x・y) )
※なぜ?→証明
[性質3:正値性]
任意の実n次元数ベクトルx∈Rnにたいして、x・x≧0 であって、
x・x=0となるのはxが零ベクトルである場合のみに限る。
すなわち、∀x∈Rn ( ( x・x≧0 ) かつ ( x・x=0⇔x=〇) ) あるいは、∀x∈Rn ( ( x・x≧0 ) かつ ( x≠〇⇒x・x>0) )
※だから、自分自身と直交する実n次元数ベクトルは、零ベクトルだけ。
※なぜ?→証明
[性質4:対称性]
任意のx,y∈Rnにたいして、x・y=y・x
すなわち、∀x,y∈Rn ( x・y=y・x )
※なぜ?→証明
【文献】
神谷浦井『経済学のための数学入門』§3.2.3(p.124);砂田『行列と行列式』§7.1(p.238);志賀『ベクトル解析30講』第11講(pp.80-81):なぜ数ベクトル空間でこのような内積が使われるのかまで説明;
斎藤『線形代数入門』2章[6.1](p.61);4章§6例1(p.120);永田『理系のための線形代数の基礎』4.1(p.113-4);佐武『線形代数学』Ⅰ§6(p.31);草場『線形代数』§5.1(p.127);杉浦『解析入門I』I§4命題4.2(p.36);布川『線形代数と凸解析』定義4.1例4.1(p.64);佐和『回帰分析』2.1.4内積と射影(p.21)柳井竹内『射影行列・一般逆行列・特異値分解』§1.1.1(p.2)
定理:(自然な)内積は、内積の定義を満たし、計量実ベクトル空間を設定する。
[神谷浦井『経済学のための数学入門』§3.2.3(p.124);砂田『行列と行列式』§7.1(p.238)
志賀『ベクトル解析30講』第11講(pp.80-81):なぜ数ベクトル空間でこのような内積が使われるのかまで説明;
斎藤『線形代数入門』2章[6.1](p.61);4章§6例1(p.120);永田『理系のための線形代数の基礎』4.1(p.113-4);
佐武『線形代数学』Ⅰ§6(p.31);]
(舞台設定)
R:実数体R
Rn:実n次元数ベクトル空間
x, y:実n次元数ベクトル
具体的に書くと、x1, x2, …, xn∈Rとして、x=( x1, x2, …, xn )∈Rn
y1, y2, …, yn∈Rとして、y=( y1, y2, …, yn )∈Rn
(本題)
・実n次元数ベクトルx, yの(自然な)内積x・yは、
実n次元数ベクトル空間Rnにおける内積〈 x, y 〉の定義を満たし、
(つまり、(自然な)内積x・yは、内積〈 x, y 〉の一例)
したがって、(自然な)内積が定義された実n次元数ベクトル空間Rnも、
計量実ベクトル空間(計量線形空間・内積空間)の定義を満たす。
※なぜ?→自然な内積の線形性・正値性・対称性は、内積〈 x, y 〉の定義そのもの。
※(自然な)内積以外の内積〈 x, y 〉の例については、
ホフマン・クンツェ『線形代数学II』8.1例1(p.92)を参照。
定義:実n次元数ベクトル空間におけるユークリッドノルム
[神谷浦井『経済学のための数学入門』§3.2.3(p.121-2);砂田『行列と行列式』§7.1(pp.241-2);
松坂『集合・位相入門』§5-B例1(pp.277-8);矢野『距離空間と位相構造』1.1.1例1.3(pp.4-5)
志賀『ベクトル解析30講』第11講(pp.80-81);佐武『線形代数学』Ⅰ§6(p.33);草場『線形代数』定義5.1(p.127);
斎藤『線形代数入門』2章§6(p.62);4章§6例1(p.120);永田『理系のための線形代数の基礎』4.1(p.114);
杉浦『解析入門I』I§4(p.36);;西村『経済数学早わかり』2章§1.4(p.33);布川『線形代数と凸解析』定義4.3(p.66);;
佐和『回帰分析』2.1.4内積と射影(p.21)柳井竹内『射影行列・一般逆行列・特異値分解』§1.1.1(p.1;4) ]
(舞台設定)
R:実数体R
Rn:実n次元数ベクトル空間
v:実n次元数ベクトル。
具体的に書くと、v1, v2, …, vn∈Rとして、v=( v1, v2, …, vn )∈Rn
x・y:実n次元数ベクトルx, yの(自然な)内積。これによって、Rnは計量実ベクトル空間となる。
(本題)
1. 任意の実n次元数ベクトルv=( v1, v2, …, vn )∈Rn にたいして、
∥v∥=「v・vの負でない平方根」
と定義する。
つまり、
∀v=( v1, v2, …, vn )∈Rn にたいして、
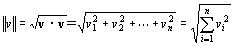
と定義する。
2. 上記の∥v∥は、次の性質をもち、実n次元数ベクトル空間におけるノルムの定義を満たす。
(1) 非負性 任意のv∈Rnにたいして、∥v∥≧0 であって、
∥v∥=0となるのはvが零ベクトルである場合のみに限る。
論理記号で表すと、(∀v∈Rn) ( ( ∥v∥≧0 ) かつ (∥v∥=0⇔v=〇) )
あるいは、(∀v∈Rn) ( ( ∥v∥≧0 ) かつ (v≠〇⇒∥v∥>0) )
(2) 線形性 任意のv∈Rnと任意の実数aにたいして、∥av∥=|a|∥v∥
論理記号で表すと、(∀v∈Rn) (∀a∈R) (∥av∥=|a|∥v∥ )
(3) 三角不等式 任意のx,y∈Rnにたいして、∥x+y∥≦∥x∥+∥y∥
※ただし、不等式左辺の+は実n次元数ベクトル空間に定義されたベクトル和、
不等式右辺の+は、実数の足し算。
論理記号で表すと、(∀x,y∈Rn) ( ∥x+y∥≦∥x∥+∥y∥ )
※なぜ?
・∥v∥は、自然な内積の正値性と∥v∥の定義により、(1)非負性を満たす。
・∥v∥は、内積の性質によって、(2)線形性を満たす。
・∥v∥は、内積の性質によって、(3)三角不等式を満たす。
3. 上記の∥v∥を、ユークリッドノルムと呼ぶ。
実n次元数ベクトル空間において単に「ノルム」といえば、このユークリッドノルムを指すのが普通。
4. ユークリッドノルムをノルムとして指定してやることによって、
ノルム空間( Rn , ∥ ∥ )が設定される。
5. 定義より、∥v∥2=v・v であるから、
実n次元数ベクトルx, yが横ベクトルのとき、
行列の積を用いて、∥v∥2= v・v=vtv=( v1, v2, …, xn )t( y1, y2, …, yn )
実n次元数ベクトルx, yが縦ベクトルのとき、
行列の積を用いて、∥v∥2= v・v=tvv
とも表せる。
※上位概念:実n次元数ベクトル空間における内積により定まるノルム、一般の計量実ベクトル空間における内積により定まるノルム
定義:ユークリッドノルムから定められる距離・ユークリッド距離
[神谷浦井『経済学のための数学入門』§3.2.3(p.123);松坂『集合・位相入門』§5-A(p.277);
矢野『距離空間と位相構造』1.1.1距離関数(p.5);志賀『固有値問題30講』8講(p.61);
杉浦『解析入門I』I§4(pp.37-8);;柳井竹内『射影行列・一般逆行列・特異値分解』§1.1.1(p.2) ]
(舞台設定)
R:実数体R
Rn:実n次元数ベクトル空間
x, y:実n次元数ベクトル
具体的に書くと、x1, x2, …, xn∈Rとして、x=( x1, x2, …, xn )∈Rn
y1, y2, …, yn∈Rとして、y=( y1, y2, …, yn )∈Rn
x・y:実n次元数ベクトルx, yの(自然な)内積。これによって、Rnは計量実ベクトル空間となる。
∥x∥:計量実ベクトル空間Rnにおけるユークリッドノルム((自然な)内積を用いて定義される)
(Rn,∥∥):計量実ベクトル空間Rnに、内積により定義されたユークリッドノルム∥ ∥を定義した、
ノルム空間
(本題)
1.
任意の実n次元数ベクトルx, yに対し、
d(x, y)=∥x-y∥
とおくと、d(x, y)は、Rnにおけるx, y間の距離の定義を満たす。
∵ノルムから定められた距離一般は距離の定義を満たす(∵)。
d(x, y) は、ノルムから定められた距離の定義を満たす
(∵ユークリッドノルムはノルムの定義を満たす)。
したがって、d(x, y) は、距離の定義を満たす。
2.
d(x, y)=∥x-y∥ を、ユークリッドノルムから定められる距離という。
3.
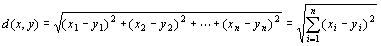
となる。
つまり、ユークリッドノルムから定められる距離は、ユークリッド距離にほかならない。
なぜなら、
d(x, y)=∥x-y∥ =∥( x1, x2, …, xn )-( y1, y2, …, yn )∥
=∥( x1, x2, …, xn )+( -y1, -y2, …, -yn )∥ ∵逆ベクトルの定義
=∥( x1-y1, x2-y2, …, xn-yn )∥ ∵ベクトル和の定義
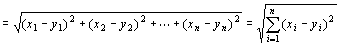
∵ユークリッドノルムの定義
※上位概念:実n次元数ベクトル空間におけるノルムから定められた距離、一般の計量実ベクトル空間においてノルムから定められる距離
定理:計量実ベクトル空間、ノルム空間、距離空間・ユークリッド空間
[神谷浦井『経済学のための数学入門』§3.2.3(p.123);松坂『集合・位相入門』§5-A(p.277);
矢野『距離空間と位相構造』1.1.1距離関数(p.5);志賀『固有値問題30講』8講(p.63);
砂田『行列と行列式』§7.1(a)定理7.9 (pp.240-1).]
(舞台設定)
R:実数体R
Rn:実n次元数ベクトル空間
x, y:実n次元数ベクトル
具体的に書くと、x1, x2, …, xn∈Rとして、x=( x1, x2, …, xn )∈Rn
y1, y2, …, yn∈Rとして、y=( y1, y2, …, yn )∈Rn
x・y:実n次元数ベクトルx, yの(自然な)内積。これによって、Rnは計量実ベクトル空間となる
∥x∥:計量実ベクトル空間Rnにおけるユークリッドノルム((自然な)内積を用いて定義される)
(Rn,∥∥):計量実ベクトル空間Rnに、内積により定義されたユークリッドノルム∥ ∥を定義した、
ノルム空間
(本題)
次の手順で、実n次元数ベクトル空間Rnからユークリッド空間をつくることができる。
Step1: 実n次元数ベクトル空間Rnに、(自然な)内積を定義して、Rnを計量実ベクトル空間とする。
Step2: 計量実ベクトル空間Rnに、(自然な)内積を用いてユークリッドノルム∥ ∥を定義して、
Rnにノルム空間(Rn , ∥ ∥ )を設定する。
Step3: ノルム空間(Rn , ∥ ∥ )に、ユークリッドノルム∥ ∥を用いてユークリッド距離dを定義して、
距離空間(Rn,d )、すなわちユークリッド空間を設定する。
※実n次元数ベクトル空間Rnがユークリッド空間と、ことわりなく、呼ばれる場合、
暗黙の了解事項として、(自然な)内積、ユークリッドノルム、ユークリッド距離が定義されている。
※上位概念:内積から定まるノルム一般を用いたRn上のノルム空間の設定・ノルムから定められる距離一般を用いたRn上の距離空間の設定、一般の計量実ベクトル空間からのノルム空間・距離空間の設定
定義:直交する orthogonal
[斎藤『線形代数入門』4章§6計量線形空間(p.120);神谷浦井『経済学のための数学入門』§3.2.3(p.125);
永田『理系のための線形代数の基礎』4.1(p.114);志賀『ベクトル解析30講』第11講(p.80);
志賀『固有値問題30講』9講(p.67);草場『線形代数』§5.1(p.129);
杉浦『解析入門I』I§4注意1(p.37);布川『線形代数と凸解析』定義4.4(p.68);
佐和『回帰分析』2.1.4内積と射影(p.21); 。]
(舞台設定)
R :実数体R
Rn:実n次元数ベクトル空間
x, y:実n次元数ベクトル
具体的に書くと、x1, x2, …, xn∈Rとして、x=( x1, x2, …, xn )∈Rn
y1, y2, …, yn∈Rとして、y=( y1, y2, …, yn )∈Rn
x・y:実n次元数ベクトルx, yの(自然な)内積。これによって、Rnは計量実ベクトル空間となる。
∥x∥:計量実ベクトル空間Rnにおけるユークリッドノルム((自然な)内積を用いて定義される)
d (x, y):ユークリッドノルムから定められたユークリッド距離
(Rn,d ):n次元ユークリッド空間
(本題)
・n次元ユークリッド空間(Rn,d )において実n次元数ベクトルx,yが直交するとは、
実n次元数ベクトルx,yの自然な内積がゼロであるということ。
・実n次元数ベクトルx,yが直交することを、記号「x⊥y」で表す。
・つまり、n次元ユークリッド空間においては、x⊥y ⇔ x・y=x1y1+ x2y2+…+xnyn=0
※自分自身と直交する実n次元数ベクトルは、零ベクトルだけ。→自然な内積の正値性
※上位概念:一般の計量実ベクトル空間における直交、内積一般による計量実ベクトル空間Rnにおける直交
※活用例:直交系、正規直交系、直交基底、正規直交基底
定義:ベクトルのなす角angle
[永田『理系のための線形代数の基礎』4.1(p.115);志賀『ベクトル解析30講』第11講(pp.79-80);
杉浦『解析入門I』I§4注意1(p.37);草場『線形代数』§5.1(p.129);;;
佐和『回帰分析』2.1.4内積と射影(p.21);柳井竹内『射影行列・一般逆行列・特異値分解』定義1.1(p.2) ]
(舞台設定)
R :実数体R
Rn:実n次元数ベクトル空間
x, y:実n次元数ベクトル
具体的に書くと、x1, x2, …, xn∈Rとして、x=( x1, x2, …, xn )∈Rn
y1, y2, …, yn∈Rとして、y=( y1, y2, …, yn )∈Rn
x・y:実n次元数ベクトルx, yの(自然な)内積。これによって、Rnは計量実ベクトル空間となる。
∥x∥:計量実ベクトル空間Rnにおけるユークリッドノルム((自然な)内積を用いて定義される)
d (x, y):ユークリッドノルムから定められたユークリッド距離
(Rn,d ):n次元ユークリッド空間
(本題)
・
※上位概念:一般の計量実ベクトル空間における直交、内積一般による計量実ベクトル空間Rnにおける角
定義:単位ベクトル
[砂田『行列と行列式』§7.1(pp.241-2);]
(舞台設定)
R:実数体R
Rn:実n次元数ベクトル空間
x, y:実n次元数ベクトル
具体的に書くと、x1, x2, …, xn∈Rとして、x=( x1, x2, …, xn )∈Rn
y1, y2, …, yn∈Rとして、y=( y1, y2, …, yn )∈Rn
x・y:実n次元数ベクトルx, yの(自然な)内積。これによって、Rnは計量実ベクトル空間となる。
∥x∥:計量実ベクトル空間Rnにおけるユークリッドノルム((自然な)内積を用いて定義される)
d (x, y):ユークリッドノルムから定められたユークリッド距離
(Rn,d ):n次元ユークリッド空間
(本題)
n次元ユークリッド空間(Rn,d )における単位ベクトルとは、
ユークリッドノルム∥x∥=1
すなわち、
∥x∥2 = x12+x22+…+ xn2 = 1
を満たす実n次元数ベクトルx のこと。
定理:単位ベクトル化
[永田『理系のための線形代数の基礎』補題4.2.1(p.116);]
(舞台設定)
R:実数体R
Rn:実n次元数ベクトル空間
x, y:実n次元数ベクトル
具体的に書くと、x1, x2, …, xn∈Rとして、x=( x1, x2, …, xn )∈Rn
y1, y2, …, yn∈Rとして、y=( y1, y2, …, yn )∈Rn
x・y:実n次元数ベクトルx, yの(自然な)内積。これによって、Rnは計量実ベクトル空間となる。
∥x∥:計量実ベクトル空間Rnにおけるユークリッドノルム((自然な)内積を用いて定義される)
d (x, y):ユークリッドノルムから定められたユークリッド距離
(Rn,d ):n次元ユークリッド空間
(本題1)
任意の実n次元数ベクトルx∈Rnについて、
xが零ベクトルでないならば、
「xのユークリッドノルムの逆数(スカラーになる)」と、実n次元数ベクトルxとのスカラー積
( 1/∥x∥ ) x
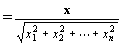
は、
n次元ユークリッド空間(Rn,d )における単位ベクトルとなる。
以上を論理記号でかくと、
(∀x∈Rn)( x≠〇 ⇒ ∥ ( 1/∥x∥ ) x ∥=1 )
(本題2)
( 1/∥x∥ ) xをつくることを、xの単位ベクトル化という。
※どうして、∥ ( 1/∥x∥ ) x ∥=1 といえるのか?→詳細
※どうして、( 1/∥x∥ ) xは、xと直交する全ての実n次元数ベクトルと直交するといえるのか?
・ユークリッドノルムの非負性より、 x≠〇ならば、∥x∥>0
したがって、 x≠〇ならば、1/∥x∥>0 …(1)
・{( 1/∥x∥ ) x }・y =( 1/∥x∥ ) ( x・y)=( x・y)/∥x∥ …(2)
∵自然な内積の線形性2
・ x≠〇 かつ x・y=0 ならば、任意の実n次元数ベクトルx,yにたいして、(1)(2)と x・y=0より、
{( 1/∥x∥ ) x }・y =0
が成り立つ。
つまり、x≠〇ならば、xと直交する全ての実n次元数ベクトルと、( 1/∥x∥ ) xは、xと直交する。
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、項目317バナッハ空間(pp.922-):ノルムとノルム空間の解説が含まれている;項目341ヒルベルト空間B.(pp.1006-7):内積の定義が含まれている.
線形代数のテキスト
ホフマン・クンツェ『線形代数学II』8.1内積(pp.91-7)、培風館、1976年。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、4.1内積(p.114);。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§6ベクトル空間の公理化(p.117)。
志賀浩二『数学30講シリーズ:線形代数30講』朝倉書店、1988年。
志賀浩二『数学30講シリーズ:ベクトル解析30講』朝倉書店、1988年、第11講(pp.78-80)。
藤原毅夫『理工系の基礎数学2:線形代数』岩波書店、1996年。
斎藤正彦『線形代数入門』東京大学出版会、1966年、4章§6計量線形空間(p.120)。
砂田利一『現代数学への入門:行列と行列式』2003年、§7.1-(a)内積 (pp.238-9).
草場公邦『線形代数(増補版)』(森毅、斉藤正彦責任編集『すうがくぶっくす』2巻)朝倉書店、1999年、5.1(pp.127-130)。
柳井晴夫・竹内啓『UP応用数学選書10:射影行列・一般逆行列・特異値分解』 東京大学出版会、1983年、§1.1.1。
木村英紀『線形代数:数理科学の基礎』東京大学出版会、2003年、3.3内積とノルム(p.55)。
解析学のテキスト
杉浦光夫『解析入門I』東京大学出版会、1987年、I章§4(pp.33-38)。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§3.2.3(p.124)。
布川昊,谷野哲三,中山弘隆『線形代数と凸解析』コロナ社、1991年、4.1.1内積と直交(pp.65-70)。
数理統計学のテキスト
佐和隆光『回帰分析』 朝倉書店、1979年、2.1ベクトルとベクトル空間。
久米均『数理統計学』コロナ社、1984年、1.線形代数1.6.計量ベクトル空間(p.6)。
![]()
![]()