|
��[�g�s�b�N�ꗗ�F���1�ϐ����ƈ��2�ϐ����Ƃ̍�����]�@ �����ڎ� |
|
��[�g�s�b�N�ꗗ�F���1�ϐ����ƈ��2�ϐ����Ƃ̍�����]�@ �����ڎ� |
|
��[�g�s�b�N�ꗗ�F���1�ϐ����ƈ��2�ϐ����Ƃ̍�����]�@ �����ڎ� |
|
��[�g�s�b�N�ꗗ�F���1�ϐ����ƈ��2�ϐ����Ƃ̍�����]�@ �����ڎ� |
|
��[�g�s�b�N�ꗗ�F���1�ϐ����ƈ��2�ϐ����Ƃ̍�����]�@ �����ڎ� |
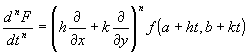
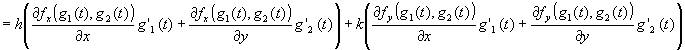
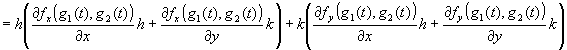
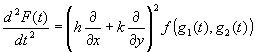
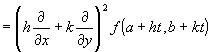
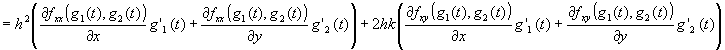
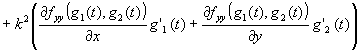 �@���������̔���
�@���������̔���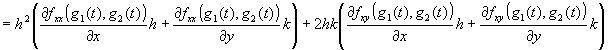
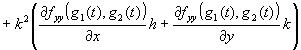
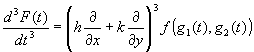
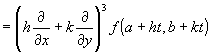
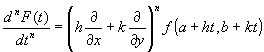
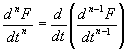
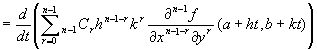
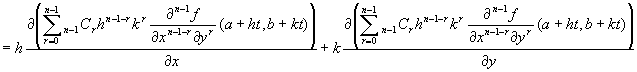
|
��[�g�s�b�N�ꗗ�F���1�ϐ����ƈ��2�ϐ����Ƃ̍�����]�@ �����ڎ� |