R2上の閉区間・閉矩形(長方形)K={ (x ,y ) | a≦x≦b, c≦y≦d }=[a,b]×[c,d] }があるとする。
(→下図黄色部分)
閉区間 [a,b]を、a=x0<x1<x2<…<xm-1<xm=bを分点としたm個の小閉区間に分割し
― つまり、[a,b]を、I1=[a,x1], I2=[x1,x2],…,Im=[xm-1,b] (a=x0<x1<x2<…<xm-1<xm=b)に分割し―、
閉区間 [c,d]を、c=y0<y1<y2<…<yn-1<yn=dを分点としたn個の小閉区間に分割することで、
― つまり、[c,d]を、J1=[a, y1], J2=[y1,y2],…,Jn=[yn-1,b] (c=y0<y1<y2<…<yn-1<yn=d)に分割することで―
mn個の小矩形subrectangle Kij = Ii × Jj ={ (x,y) | xi-1≦x≦xi , yj-1≦y≦yj } (i=1,2,…,m、 j=1,2,…,n ) に、
矩形Kは分割される。
これを矩形の分割a partition of the rectangleないし矩形網[高木『解析概論』]と呼び、記号⊿で表す。
また、Kを小矩形Kij(i=1,2,…,m、 j=1,2,…,n )にわける線分を、
⊿の分割線[黒田『微分積分』347.]、⊿の割線[吹田新保『理工系の…』190ページ23行以降]
などとよぶ。

分割のメッシュの細かさを示す指標として、以下の二つがとりあげられる。
これらは、記号|⊿|、δなどで表される。
(杉浦『解析入門I』207:は1次元同様に、分割⊿の幅(mesh)と呼んでいる。)
1.すべての小矩形の最長辺 [高木『解析概論』p.325;吹田,新保『理工系の微分積分学』189;.]
すなわち、xi- xi-1 (i=1,2,…,m)とyj-yj-1 (j=1,2,…,n) すべてのなかの最大値、
2. 小矩形の直径の最大値
[小平『解析入門II』317;黒田『微分積分』347;杉浦『解析入門I』207:n次元区間一般]
すなわち、mn個ある小矩形Kij (i=1,2,…,m、 j=1,2,…,n ) の対角線
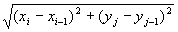
のなかの、最大値。
定義:リーマン和 Riemann sum
[高木『解析概論』p.325-6;小平『解析入門II』317-8;吹田,新保『理工系の微分積分学』189;黒田『微分積分』348.
杉浦『解析入門I』207:n次元区間一般]
cf.1変数関数のリーマン和・スチルチェス和、
(舞台設定)
K: Kは、R2上の閉区間 { (x ,y ) | a≦x≦b, c≦y≦d }=[a,b]×[c,d]を表すとする。
Kij: Kの分割⊿によってできたmn個の小矩形を
Kij ={ (x ,y ) | xi-1≦x≦xi , yj-1≦y≦yj }=[ xi-1, xi ]×[ yj-1, yj ] (i=1,2,…,m, j=1,2,…,n )
ただし、x0= a, xm=b, y0= c, yn =dとする。
で表すとする。
f(x ,y ): ここでは、関数f(x ,y )として、Kの上で定義された有界関数のみを考える。
(本題)
まず、 Kij (i=1,2,…,m, j=1,2,…,n )の各々から、
代表点Pij =(ζij ,ηij )∈Kij ={ (x,y) | xi-1≦x≦xi , yj-1≦y≦yj }を一つ、勝手に選ぶ。(下図参照)

以下のように、積:f (Pij )・(Kijの面積)=f (ζij ,ηij )( xi- xi-1)(yj- yj-1)
を、mn個全てのKij (i=1,2,…,m, j=1,2,…,n )について足し合せる。

これを、
関数fの 、(分割⊿・代表点{ Pij }とした際の)リーマン和 Riemann sum
という。
※分割⊿、代表点{ Pij }のとりかたは、いろいろであるから、
関数fのリーマン和は、
分割⊿、代表点{ Pij }のとりかたに応じて、値を変えうる。
つまり、関数fのリーマン和は、分割⊿、代表点{ Pij }のある種の関数となっている。
分割を細かくしていったときに、この関数が収束するかどうかという問題が、
下記の積分可能の有無の問題に他ならない。
定義:(閉矩形)上で積分可能、2重積分 double integral
[吹田・新保『理工系の微分積分学』189; 高木『解析概論』p.325-6。
※小平『解析入門II』317-20;黒田『微分積分』348.は連続関数に限定して議論するゆえ、すべて可積分に。]
(舞台設定)
K: Kは、R2上の閉区間 { (x ,y ) | a≦x≦b, c≦y≦d }=[a,b]×[c,d]を表すとする。
f(x ,y ): ここでは、関数f(x ,y )として、Kの上で定義された有界関数のみを考える。
(本題)
Kの分割⊿を限りなく細かくしていくと、
分割⊿の取り方、それによってできた小矩形 Kijの代表点Pij (i=1,2,…,m, j=1,2,…,n )の取り方によらず、
f(x ,y )のリーマン和R[ f ; ⊿ ; {Pij } ] が一定値J に収束するとき、
( すなわち、|⊿|→0で、R[ f ; ⊿ ; {Pij } ] → Jとなるとき、)
※正確に書けば、
任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
分割⊿の取り方、
それによってできた小矩形 Kijの代表点Pij (i=1,2,…,m, j=1,2,…,n )の取り方によらず、
|R[ f ; ⊿ ; {Pij } ]-J|<ε 」
を成り立たせる、ある正の実数δが存在するとき、
※これを、記号で表すとR[ f ; ⊿ ; {Pij } ] → J(|⊿|→0)
ないし、
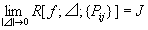 、
、
f はK上でリーマン積分可能、リーマン可積分である、という。
また、このとき、値Jを
1.
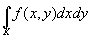
と書いて、「 f のK上の(あるいはKにおける)積分」と呼ぶ。
あるいは、
2.
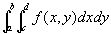
と書いて、「 f のK上の(あるいはKにおける) 重積分(あるいは2重積分)」と呼ぶ。
また、Kを積分範囲[黒田『微分積分』348.]と呼ぶ。
※もちろん、
(i) |⊿|→0で、R[ f ; ⊿ ; {Pij } ] → Jとなって積分可能となる場合もあれば、
(ii) |⊿|→0で、R[ f ; ⊿ ; {Pij } ] → Jとならず、積分可能とならない場合もある。
いかなる条件下で、(ii)ではなく、(i)となるのかについては、
リーマン可積分条件を見よ。
( reference )
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、202項積分法(pp.520-525)→リーマン積分、
高木貞治『解析概論:改訂第3版』岩波書店、1983年、第8章90-92節pp.325-332. .
吹田・新保『理工系の微分積分学』学術図書出版社、1987年、第7章1節(pp.189-196).
小平邦彦『解析入門II』 (軽装版)岩波書店、2003年、第7章(pp.317-330.)。連続関数に限定
黒田成俊『21世紀の数学1:微分積分』共立出版、2002年、第10章1節(pp.346-352.)。連続関数に限定。
高橋一『経済学とファイナンスのための数学』新世社、1999年、第3章3.8節I(pp. 106-108):矩形上ではなく、いきなり一般の積分範囲上。
杉浦光夫『解析入門I』東京大学出版会、1980年、pp.205-229:矩形上;pp.254-279:一般の積分範囲。(2重積分についてというよりもむしろ、主にn変数関数全般についてリーマン積分を論じている。)
Walter Rudin,Principles of Mathematical Analysis,Mcgraw-Hill,1953-1976.
=ウォ-ルタ-・ルディン『現代解析学』共立出版、1971年、第6章。
高橋陽一郎『岩波講座現代数学への入門:微分と積分2』 岩波書店、1995年、5章2節(pp.138-146.):。このテキストは、リーマン積分とルベーク積分の間という特殊な立場を進んで行っている気がする。ついていってよいのかどうか。
片山孝次『微分積分学』(現代数学レクチャーズB-8)、培風館、1980年、p.202.極めて簡潔な要約。
和達三樹『理工系の数学入門コース1:微分積分』岩波書店、1988年、pp.138-9. アイデアだけ。厳密な議論なし。
小形正男『理工系数学のキーポイント7:多変数の微分積分』岩波書店、1996、87-89. アイデアだけ。厳密な議論なし。
Lang,Serge.Undergraduate Analysis(Undergraduate
Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg
Tokyo,1983,Chapter 19. Multiple Integrals. (pp.468-482.)。

