陰関数定理
→参考文献・総目次
I.
2変数で方程式が1つのケース。
陰関数の存在の十分条件
[吹田新保『理工系の微分積分学』169-170; 小形『多変数の微分積分』201-204.神谷浦井『経済学のための数学入門』239-240.]
[設定]
点
P0(x0,y0)の近傍で定義されたC1級関数で、
点P0(x0,y0)においてゼロをとる関数F(x,y) を考える。
(すなわち、F (x0,y0) = 0 )
[本題1]
点P0におけるyについての偏微分係数Fy(x0,y0)≠0ならば、
x= x0を含む適当な開区間Iと正数δをとれば、
各x∈Iに対して、
F (x,y) = 0、|y− y0|<δを満たすyがただ一つ定まり、
I上の関数y=f(x)とできる。
[本題2:陰関数の導関数]
このI上の関数y=f(x)はC1級であり、
f'(x)=−Fx ( x, f(x) ) / Fy ( x, f(x) )
[証明]→吹田新保『理工系の微分積分学』170-171:非常に丁寧。;
[本題3:]
上の定理において、関数F(x,y) がCn級関数ならば、
y=f(x)もCn級関数となる。
II. 3変数で方程式が1つのケース。
陰関数の存在の十分条件
[吹田新保『理工系の微分積分学』171]
[設定]
点
P0(x0,y0,z0)の近傍で定義されたC1級関数で、
点P0(x0,y0,z0)においてゼロをとる関数F(x,y,z) を考える。
(すなわち、F (x0,y0,z0) = 0 )
[本題1]
点P0におけるzについての偏微分係数Fz(x0,y0,z0)≠0ならば、
点 (x0,y0)の適当な近傍Uをとれば、
U上のC1級関数z=f(x,y)で、
z0=f(x0,y0)
F(x,y, f(x,y))=0 ( (x,y)∈U )
を満たすものがただ一つ存在する。
[本題2:陰関数の導関数]
∂f/∂x =−Fx ( x,y, f(x,y) ) / Fz (x,y, f(x,y))
∂f/∂y =−Fy ( x,y, f(x,y) ) / Fz (x,y, f(x,y))
[本題3:]
上の定理において、関数F(x,y,z) がCn級関数ならば、
y=f(x,y)もCn級関数となる。
III.
m変数で方程式が2つのケース[小形『多変数の微分積分』204-205.]
[設定]
g1(x1,x2,…,xm,y1,y2)=0
g2(x1,x2,…,xm,y1,y2)=0
となる二つのC1級関数g1(x1,x2,…,xm,y1,y2)、g2(x1,x2,…,xm,y1,y2)を考える。
[本題1]
関数g1 g2のx1,x2,…,xmを固定してあらわに書かないで、y1,y2の関数として書きなおしたものを、
G1(y1,y2)=z1, G2(y1,y2)=z2 とおく。
G1(y1,y2)=z1, G2(y1,y2)=z2のヤコビアンが非ゼロ、つまり、
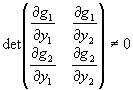
ならば、陰関数y1=f1(x1,x2,…,xm), y2=f2(x1,x2,…,xm) が一意的に与えられる。
[本題3:]
上の定理において、関数g1(x1,x2,…,xm,y1,y2)、g2(x1,x2,…,xm,y1,y2)がCn級関数ならば、
f1(x1,x2,…,xm), f2(x1,x2,…,xm)もCn級関数となる。
VI.
m変数で方程式がn個のケース[神谷浦井『経済学のための数学入門』239-244.]
(
reference)
経済数学系
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、pp.239-244. 逆関数定理(1変数関数→n変数関数)→陰関数定理(1変数関数→n変数関数)→比較静学
Chiang, Fundamental Methods of Mathematical Economics: Third Edition, McGraw Hill,1984、pp.204-214陰関数定理→比較静学
西村和雄『経済数学早わかり』日本評論社、1982年、pp.130-132:陰関数の微分;148-153:陰関数定理→ラグランジュ乗数法。
岡田章『経済学・経営学のための数学』東洋経済新報社、2001年、pp.130-135。
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.152-4。
理工系向け数学教科書
小形正男『理工系数学のキーポイント7:多変数の微分積分』岩波書店、1996、pp. 201-205. 逆関数定理→陰関数定理→ラグランジュ未定乗数法
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.169-172;p.261.
解析学入門書
高木貞治『解析概論 改訂第三版』岩波書店、1983年、pp. 294-299.
小平邦彦『解析入門II』(軽装版)岩波書店、2003年、pp.393-402。
高橋陽一郎『岩波講座現代数学への入門:微分と積分2』 岩波書店、1995年、pp.105-115。
杉浦光夫『解析入門II』岩波書店、1980年、pp.3-16.
住友洸(たけし)『
大学一年生の微積分学』現代数学社、1987年,pp.98-100「逆写像存在定理」。