���Δ����\/�W���̌����@
���Δ����\/�W���̒�`
���Δ����\/�W���̑��쉻1�@
���Δ����\/�W���̑��쉻2
���Δ����\/�W���̌v�Z
���ӁF�_( x0, y0 )�ɂ����� f (x,y) ��x�Ɋւ���Δ����\/�Δ����W��
�@step1.
�@step4. |
|
���ӁF�_( x0, y0 )�ɂ����� f (x,y) ��y�Ɋւ���Δ����W��
�@step1.
�@step2.
�@step4.
|
|
���Δ����\/�W���̐}���@ ���Δ����\/�W���̌����@ ���Δ����\/�W���̒�` ���Δ����\/�W���̑��쉻1�@ ���Δ����\/�W���̑��쉻2 ���Δ����\/�W���̌v�Z |
����L�́u�Δ����\�v�u�Δ����W���v�̌��ӂ́A
�@�@1�ϐ����́u�����\�v�u�����W���v�̊T�O�������āA
�@�@���̂悤�ɒ�`�����B
| �@ | �@ | |
|
|
�Ez=f (x,y )���A����R2��̂����̈�D�Œ�`���ꂽ2�� �����A �@�_ (x0, y0)���̈�D���������� ���_�Ƃ���B�@ �Ey��y0�ɌŒ肵��x������1�� �����Ƃ���f (x, y0)���A �@x = x0�ɂ����āAx�ɂ��������\�ł��邱�Ƃ��A �@�@�uf (x,y )���_ (x0, y0)�ɂ�����x�ɂ��ĕΔ����\partially differentiable�v �@�Ƃ����A�@ �@x��1�� ����f (x, y0)��x = x0�ɂ����������W�����A �@�@�u�_ (x0, y0)�ɂ�����f (x,y )�� �@�@�@�@�@x�Ɋւ����Δ����W�� partially differential coefficient�v �@�Ƃ�ԁB �@�u�_( x0, y0 )�ɂ�����f (x,y )��x�Ɋւ���Δ����W���v���A �@�ȉ��̋L���ŕ\���B �@�@�@ �@�@�@ f x ( x0, y0 )�@ �Ex��x0�ɌŒ肵��y������1�� �����Ƃ���f (x0, y)���A �@y = y0�ɂ����āAy�ɂ��������\�ł��邱�Ƃ��A �@�@�uf (x,y )���_(x0, y0)�ɂ�����y�ɂ��ĕΔ����\partially differentiable�v �@�Ƃ����A�@ �@x��1�� ����f (x0, y)��y= y0�ɂ����������W�����A �@�@�u�_ (x0, y0)�ɂ�����f (x,y ) �� �@�@�@�@y�Ɋւ����Δ����W�� partially differential coefficient�v �@�Ƃ�ԁB �@�u�_( x0, y0 )�ɂ�����f (x,y )��y�Ɋւ���Δ����W���v���A �@�ȉ��̋L���ŕ\���B �@�@�@�@ 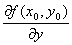 �@�@�@�@ f y ( x0, y0 )�@ ��1�ϐ����́u�����\�v�u�����W���v�̓�ʂ�̑��쉻�ɏ]���āA �@�u�Δ����\�v�u�Δ����W���v�̒�`���A �@��ʂ�ɑ��쉻�����B�@�@ |
[����] �E���c�w�o�ϊw�E�o�c�w�̂��߂̐��w�x1.6(p.42) �E���J�v��w�����o�ϊw�����x��` 7.1(p.163) �Fn�ϐ�����.�@ �Ede la Fuente, Mathematical Methods and Models for Economists, PartI-4-2-Definition2.2 (pp.163-4) �Fn�ϐ������l��. �E���Y�w��͓����x�U��3��`2 (p.108)�Fn�ϐ�m�l�x�N�g���l���G �E���Y�w��͉��K�x�U �́�2-2.1(p. 88) �Fn�ϐ������l�� �E����u���ϐ��� ���̔���-��3���v�i������w07 �N�x�S�w���R�����[�~�i�[���j �E���E����w�o �ϊw�̂��߂̐��w�x1.3.1�Δ���(p.8). cf. 1
�ϐ����̔����W��/
n�ϐ����̕Δ���/�x�N�g���l
���̕Δ��� |
|
���Δ����\/�W���̐}���@ ���Δ����\/�W���̌����@ ���Δ����\/�W���̒�` ���Δ����\/�W���̑��쉻1�@ ���Δ����\/�W���̑��쉻2 ���Δ����\/�W���̌v�Z |
|
���쉻1 |
�E�uf (x,y )���_ (x0, y0)�ɂ�����x�ɂ��ĕΔ����\�ł���v�Ƃ́A |
| �@ |
�E�u�_( x0, y0 )�ɂ�����f (x,y )��x�Ɋւ���Δ����W���v |
| �@ |
�E�uf (x,y )���_ (x0, y0)�ɂ�����y�ɂ��ĕΔ����\�ł���v�Ƃ́A |
| �@ |
�E�u�_ ( x0, y0 )�ɂ�����f (x,y )��y�Ɋւ���Δ����W���v �@�@�@�@ 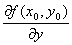 �@�@�@�@ f y ( x0, y0 )�@ �@�Ƃ́A �@�@f (x,y )���_ (x0, y0)�ɂ�����y�ɂ��ĕΔ����\�ł���Ƃ��́A �@�@�L�����Ɍ��l �@�@�@�@ 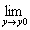 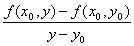 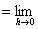 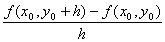 �@�@ �@�@�@�@�������B |
| �@ |
[���Δ����W���̐擪�ɖ߂�] |
|
���Δ����\/�W���̐}���@ ���Δ����\/�W���̌����@ ���Δ����\/�W���̒�` ���Δ����\/�W���̑��쉻1�@ ���Δ����\/�W���̑��쉻2 ���Δ����\/�W���̌v�Z |
|
���쉻2 |
�E�uf
(x,y )���_(x0, y0)��x�ɂ��ĕΔ����\�ł����āA |
�@ |
| �@ |
�E�uf
(x,y )���_(x0, y0)��y�ɂ��ĕΔ����\�ł����āA |
�@ |
| �@ | [���Δ����W���̐擪�ɖ߂�] |
|
|
���Δ����\/�W���̐}���@ ���Δ����\/�W���̌����@ ���Δ����\/�W���̒�` ���Δ����\/�W���̑��쉻1�@ ���Δ����\/�W���̑��쉻2 ���Δ����\/�W���̌v�Z |
|
�v�Z |
[��v�Z] |
�@ |
|
|
[Mathematica�ɑ��ĕΔ����W�����v�Z�����閽��]�@�@ |
[����] �E���ѓ����wMathematica�ɂ����ϕ��x10.2(p.93) |
|
���Δ����\/�W���̐}���@ ���Δ����\/�W���̌����@ ���Δ����\/�W���̒�` ���Δ����\/�W���̑��쉻1�@ ���Δ����\/�W���̑��쉻2 ���Δ����\/�W���̌v�Z ��[�g�s�b�N�ꗗ�F2�ϐ����̕Δ���] �����ڎ� |
��`�F���� partial derivative
�y�����z���c�w�o�ϊw�E�o�c�w�̂��߂̐��w�x1.6(p.42)/���`�w���ϐ��̔����ϕ��x22.�y��`�z
�Ez=f (x,y)���̈�D�̊e�_��x�Ɋւ����Δ����\�ł���Ƃ��A
�@�_( x0, y0 )��D�ɂ�����x�Ɋւ����Δ����W���@
�@�@
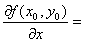
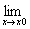
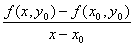
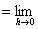
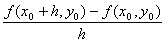
�@�̒l�́A�_( x0, y0 )�ɂ���ĕς���Ă��邩��A�̈�D����_( x0, y0 )�̊��B
�@x0, y0��x,y�Ə����������̈�D��̊�
�@�@�@�@
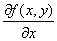
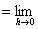
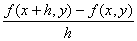
�@���Ax�Ɋւ���z=f (x,y)���Γ����ƌĂԁB
�Ez=f (x,y)���̈�D�̊e�_��y�Ɋւ����Δ����\�ł���Ƃ��A
�@�_( x0, y0 )��D�ɂ�����y�Ɋւ����Δ����W���@
�@�@
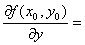
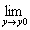
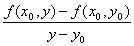
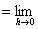
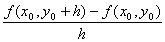
�@�̒l�́A�_( x0, y0 ) �ɂ���ĕς���Ă��邩��A�̈�D����_( x0, y0 )�̊��B
�@x0, y0 �� x,y �Ə����������̈�D��̊�
�@�@�@�@
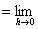
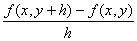
�@���Ay�Ɋւ���z=f (x,y)���Γ����ƌĂԁB
�y�L�@�z
�Ez=f (x,y) ��x�Ɋւ���Γ�����\���L���B�@
�@�@�@fx�@ zx�@�@
�@�@�@
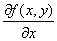 �@
�@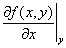 �@
�@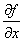 �@
�@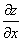 �@
�@�Ez=f (x,y) ��y�Ɋւ���Γ�����\���L���B�@
�@�@�@fx�@ zx�@�@
�@�@�@
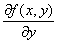 �@
�@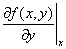 �@
�@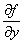 �@
�@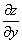 �@
�@���u�@�f��f�@�f��x�@�v�ƓǂށB
�y���z
�@�E2�ϐ����̕Γ����͓��R2�ł���B�������ׂ�ƁA���z�x�N�g���i�i�u���j�ɂȂ�B
�@�E�Δ����\�����A�����͏o�Ă��Ȃ��B�@[�����w��͓���II�xp.266]�@�@�@
�@�@�@��1�ϐ����̔����\���ƘA����/2�ϐ����̑S�����\��/2�ϐ����̘A�����@
�y�v�Z�z
[��v�Z]
�@���Ƃ��A
�@z=f (x,y)=20-x2-4y2�@��x�Ɋւ���Γ��������߂�Ȃ�A
�@1. z=f (x,y)=20-x2-4y2�@��y��萔�Ƃ݂Ȃ��A
�@�@z=f (x,y)=20-x2-4y2�@���A
�@�@�@x��1�ϐ���z=g (x)= -x2+(20-4y2)
�@�@�Ƃ��Ĉ����B
�@2. 1�ϐ����̓����̌����������āA
�@�@z=g (x)= -x2+(20-4y2)�����������߂�B
�@3. ���܂���z=g (x)= -x2+(20-4y2)������g'(x)=-2x���A
�@�@x�Ɋւ���Γ����ł���B
[Mathematica�ɑ��ĕΔ����W�����v�Z�����閽��]�@�@
�@�E���̃R�[�h�����s����ƁA�@�@f (x,y)=20-x^2-4y^2 ��x�Ɋւ���Γ�����
�@�@�v�Z�����B�@�@�@
�@�@�@�@�@�@Module[{f}, f[x_,y_]:=20-x^2-4y^2;Derivative[1,0][f][x,y]]�@�@
�@�E���̃R�[�h�����s����ƁA
�@�@�_(2,1)�ɂ�����f (x,y)=20-x^2-4y^2 ��y�Ɋւ���Γ�����
�@�@�v�Z�����B�@�@�@
�@�@�@�@�@�@Module[{f}, f[x_,y_]:=20-x^2-4y^2;Derivative[0,1][f][x,y]]�@�@
�@* ���
�@�@Derivative[n,m][f][x,y]�Ƃ́A
�@�@��f���Ax�ɂ���n�K�Ay�ɂ���m�K���Γ��������߂閽�߁B
|
��[�g�s�b�N�ꗗ�F2�ϐ����̕Δ���] �����ڎ� |
�ireference�j
���ؒ厡�w��͊T�_�@������O���x��g���X�A1983�N�A2��21�Δ���(p. 54).���{���w��ҏW�w��g���w���T�i��O�Łj�x ��g���X�A1985�N�B
��쌒���Y�E�c��ÍG�w�Љ�Ȋw�҂̂��߂̊�b���w�@�������x�։ؖ[�App.91-3.
�_�J�a��E�Y�䌛�w�o�ϊw�̂��߂̐��w�����x������w�o�ʼn�A1996�N�App.223-225.
�����M�F�w��͓���II�x (�y����)��g���X�A2003�N p.265;272.�B
�a�B�O���w���H�n�̐��w����R�[�X1�E�����ϕ��x��g���X�A1988�N�App.116-119.
���c�E�V�ہw���H�n�̔����ϕ��w�x�w�p�}���o�ŎЁA1987�N�Bpp.161-4.
���Y���v�w��͓����x��g���X�A1980�N�App.107-112. �@�������A�����Ȃ葽�����B
������w�o�ϊw�ƃt�@�C�i���X�̂��߂̐��w�x�V���ЁA1999�N�App.57-58�B
�����z��Y�w��g�u�����㐔�w�ւ̓���F�����Ɛϕ�2�x ��g���X�A1995�N�App.72-77�B
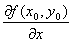 �@
�@