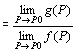2変数関数の極限の性質：トピック一覧　　

　　・極限値どおしの演算[極限値の和差/定数倍/積/商]　　
　　・コーシーの判定条件　　

　※関連ページ：1変数関数の極限の性質/ n変数関数の極限の性質/ベクトル値関数の極限の性質
　※2変数関数に関する諸概念の定義：2変数関数の諸属性/極限/連続性/偏微分/全微分/矩形上の積分/点集合上の積分　
　→参考文献・総目次

定理：2変数関数の極限値どおしの演算

舞台
設定

f,g：平面R²上の点集合D（定義域）Dに属す各点Pにたいして実数を対応づける2変数関数。
A=(x₀, y₀)：平面上の点集合D上の定点。つまり、A=(x₀, y₀)∈D⊂R²
P=(x, y)：平面上の点集合D上の動点。つまり、つまり、P=(x, y)∈D⊂R²　

定理1

→証明

[ sum-difference limit theorem ]　
f ( P )→c (P→A)かつg ( P )→d (P→A)　ならば、{f (P)±g (P)}→c+d ( P→A )
つまり、P→Aとしたときにf (P),g (P)が収束するならば、
　　　　　　　　

cf.
1変数関数の極限値どおしの演算
n変数関数の極限値どおしの演算
ベクトル値関数の極限値のベクトル和
ベクトル値関数の極限値のスカラー倍

[文献]
吹田新保『理工系の微分積分学』p.23;
小平『解析入門�U』pp.259-260:証明略
杉浦『解析入門I』定理6.6(pp.57-63)：Rⁿ→R^mの関数一般について
��木『解析概論』9極限(p.21):証明略.

定理2

→証明

f ( P )→d (P→A)　ならば、任意の実数cに対して、cf (P)→cd ( P→A )
つまり、P→Aとしたときに、f(P)が収束するならば、任意の実数cに対して、
　　　　　　　　　　　

定理3

→証明

[ product limit theorem ]　
f ( P )→c (P→A)かつg ( P )→d (P→A)　ならば、{f (P)g (P)}→cd ( P→A )
つまり、P→Aとしたときに、f (P),g (P)が収束するならば、　
　　　　　　　　　

定理4

→証明

[quotient limit theorem]　　
f ( P )→c (P→A)かつg ( P )→d (P→A)かつc≠０　ならば、{g (P)/f (P)}→d/c ( P→A )
つまり、P→Aとしたときにf (P),g (P)が収束し、
　　　　　かつ、このときのf(P)の極限値が０でないならば、　
　　　　　　　　 　

→[トピック一覧：2変数関数の極限の性質]
→総目次　

証明→定理1

P→Aとしたときにf(P)が実数値cへ収束し、かつ、g(P)が実数値dへ収束する
　　　　つまり、f ( P )→c (P→A)かつg ( P )→d (P→A)　
と仮定する。…(0)
[予備作業]
・関数の収束と点列･数列の収束を関係付ける定理より、
　f ( P )→c ( P → A )　
　　⇔　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ f (P_n)→c (n→∞)） …(1-1)
　g ( P )→d ( P → A )　
　　⇔　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ g (P_n)→d (n→∞)）…(1-2)
・2変数関数h( P )=f ( P )±g ( P )　を定義する。
　関数の収束と点列･数列の収束を関係付ける定理より、
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ h (P_n)→e (n→∞)） 　
　　⇔h ( P )→e ( P→A )　
　ここで、h( P )を、f ( P )±g ( P )に戻すと、　
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ {f (P_n)±g (P_n)}→e (n→∞)）
　　⇔　{f (P)±g (P)}→e ( P→A )　…(1-3)
・収束数列の演算則より、
　数列{ f (P₁), f (P₂), f (P₃),…}、{ g(P₁), g(P₂), g(P₃),…}について　
　　　f (P_n)→c (n→∞) かつ g(P_n)→d (n→∞)　　　　
　ならば、
　　f (P_n)±g (P_n)→c+d　 (n→∞)　　　…(1-4)
[本題]
・仮定(0)「f ( P )→c (P→A)かつg ( P )→d (P→A)」のもとで、
　　(1-1)　(1-2)　(1-4)より、
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ f (P_n)→c (n→∞)かつg (P_n)→d (n→∞)　
　　　　　　　　　　　　　　　　　　　　　　　　　　　⇒　f (P_n)±g (P_n)→c+d (n→∞)　　）
　　　…(1-5)　
・(1-5)は、(1-3)を用いて、{f (P)±g (P)}→c+d ( P→A )　と言い表せる。
　したがって、
　仮定(0)「 f ( P )→c (P→A) かつ g ( P )→d (P→A)」のもとで、
　{f (P)±g (P)}→c+d ( P→A )である　。

→戻る

証明→定理2

P→Aとしたときにf(P)が実数値dへ収束する、つまり、f ( P )→d (P→A)　
と仮定する。…(0)
[予備作業]
・関数の収束と点列･数列の収束を関係付ける定理より、
　f ( P )→d ( P → A )　
　　⇔　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ f (P_n)→d (n→∞)） …(1)
・2変数関数h( P )=cf ( P )　（cは任意の実数）を定義する。
　関数の収束と点列･数列の収束を関係付ける定理より、
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ h (P_n)→e (n→∞)） 　
　　⇔h ( P )→e ( P→A )　
　ここで、h( P )を、cf ( P )に戻すと、　
　（∀{ P_n }）（（P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒（∀c∈R）（cf (P_n)→e (n→∞)））
　　⇔　（∀c∈R）（cf (P)→e ( P→A )）　…(2)
・収束数列の演算則より、
　数列{ f (P₁), f (P₂), f (P₃),…}について、f (P_n)→d (n→∞)ならば、任意の実数cに対し、cf (P_n)→cd (n→∞)
　　（f (P_n)→d (n→∞)）⇒（（∀c∈R）（cf (P_n)→cd (n→∞)））　　　　　　　
　　　　…(3)
[本題]
・仮定(0)「f ( P )→d (P→A)」のもとで、
　　(1),(3)より、
　(∀{ P_n }) (( P_n→A (n→∞)かつ(∀n) (P_n ≠A))⇒(f (P_n)→d (n→∞))⇒(∀c∈R)(cf (P_n)→cd (n→∞)））
　　　…(4)　
・(4)は、(2)を用いて、（∀c∈R）（cf (P)→cd ( P→A )）　と言い表せる。
　したがって、
　仮定(0)「 f ( P )→d(P→A) 」のもとで、（∀c∈R）（cf (P)→cd ( P→A )）である　。

→戻る

証明→定理3

P→Aとしたときにf(P)が実数値cへ収束し、かつ、g(P)が実数値dへ収束する
　　　　つまり、f ( P )→c (P→A)かつg ( P )→d (P→A)　
と仮定する。…(0)
[予備作業]
・関数の収束と点列･数列の収束を関係付ける定理より、
　f ( P )→c ( P → A )　
　　⇔　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ f (P_n)→c (n→∞)） …(1-1)
　g ( P )→d ( P → A )　
　　⇔　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ g (P_n)→d (n→∞)）…(1-2)
・2変数関数h( P )=f ( P )g ( P )　を定義する。
　関数の収束と点列･数列の収束を関係付ける定理より、
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ h (P_n)→e (n→∞)） 　
　　⇔h ( P )→e ( P→A )　
　ここで、h( P )を、f ( P )g ( P )に戻すと、　
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ f (P_n)g (P_n)→e (n→∞)）
　　⇔　f (P)g (P)→e ( P→A )　…(2)
・収束数列の演算則より、
　数列{ f (P₁), f (P₂), f (P₃),…}、{ g(P₁), g(P₂), g(P₃),…}について　
　　　f (P_n)→c (n→∞) かつ g(P_n)→d (n→∞)　　　　
　ならば、
　　f (P_n)g (P_n)→cd　 (n→∞)　　　…(3)
[本題]
・仮定(0)「f ( P )→c (P→A)かつg ( P )→d (P→A)」のもとで、
　　(1-1)　(1-2)　(3)より、
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ f (P_n)→c (n→∞)かつg (P_n)→d (n→∞)　
　　　　　　　　　　　　　　　　　　　　　　　　　　　⇒　f (P_n)g (P_n)→cd (n→∞)　　）
　　　…(4)　
・(4)は、(2)を用いて、f (P)g (P)→cd ( P→A )　と言い表せる。
　したがって、
　仮定(0)「 f ( P )→c (P→A) かつ g ( P )→d (P→A)」のもとで、
　{f (P)g (P)}→cd ( P→A )である　。

→戻る

証明→定理4

P→Aとしたときにf(P)が実数値cへ収束し、かつ、g(P)が実数値dへ収束し、かつ、c≠０
　　　　つまり、f ( P )→c (P→A)かつg ( P )→d (P→A)かつc≠０　　
と仮定する。…(0)
[予備作業]
・関数の収束と点列･数列の収束を関係付ける定理より、
　f ( P )→c ( P → A )　
　　⇔　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ f (P_n)→c (n→∞)） …(1-1)
　g ( P )→d ( P → A )　
　　⇔　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ g (P_n)→d (n→∞)）…(1-2)
・2変数関数h( P )=g (P)/f (P)　を定義する。
　関数の収束と点列･数列の収束を関係付ける定理より、
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ h (P_n)→e (n→∞)） 　
　　⇔h ( P )→e ( P→A )　
　ここで、h( P )を、g (P)/f (P)に戻すと、　
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ g (P)/f (P)→e (n→∞)）
　　⇔　g (P)/f (P)→e ( P→A )　…(2)
・収束数列の演算則より、
　数列{ f (P₁), f (P₂), f (P₃),…}、{ g(P₁), g(P₂), g(P₃),…}について　
　　　f (P_n)→c (n→∞) かつ g(P_n)→d (n→∞)　かつ c≠０　　　
　ならば、
　　g (P_n)/f (P_n)→d/c　 (n→∞)　　　…(3)
[本題]
・仮定(0)「f ( P )→c (P→A)かつg ( P )→d (P→A)かつc≠０」のもとで、
　　(1-1)　(1-2)　(3)より、
　（∀{ P_n }）（（ P_n→A (n→∞)かつ(∀n) (P_n ≠A) ）⇒ f (P_n)→c (n→∞)かつg (P_n)→d (n→∞)　
　　　　　　　　　　　　　　　　　　　　　　　　　　　⇒　g (P_n)/f (P_n)→d/c (n→∞)　）
　　　…(4)　
・(4)は、(2)を用いて、g (P)/f (P)→d/c ( P→A )　と言い表せる。
　したがって、
　仮定(0)「 f ( P )→c (P→A) かつ g ( P )→d (P→A)かつc≠０」のもとで、
　g (P)/f (P)→d/c ( P→A )である　。

→戻る

→[トピック一覧：2変数関数の極限の性質]
→総目次　

定理：コーシーの判定条件　[P→ Aのとき]

舞台
設定

f：平面R²上で定義された2変数関数。　
A=(x₀, y₀)：平面R²上の定点。つまり、A=(x₀, y₀)∈R²
P=(x, y)：平面R²上の動点。つまり、P=(x, y)∈R²　

Cf.
　1変数関数の場合
　 n変数関数の場合
　ベクトル値関数の場合　

[文献]
小平『解析入門�U』定理6.1(pp.259-260):証明略。
杉浦『解析入門I』定理6.10(pp.61-62):証明付.
��木『解析概論』9極限(pp.22-3).

定理

次の命題S,命題T,命題Rは互いに言い換え可能である。
つまり、命題S⇔命題T⇔命題R

命題S :
　P→Aのとき、関数f (P)が収束する　
命題T :
　任意の正数εに対して、ある正数δをとると
　　任意のP,Q∈R²　にたいして、　　
　　　「（０＜d (P,A)＜δかつ０＜d (Q,A)＜δ）ならば、|f (P)−f (Q)|＜ε」
　　　　　　　　　　　　　　＊　d ( P, A )は点Pと点Aとの距離を表す。
　が成り立つ。
　論理記号では、
　(∀ε>０) (∃δ>０)
　　　(∀P,Q∈R²) ((０<d (P,A)<δかつ０<d(Q,A)<δ）⇒|f (P)−f (Q)|＜ε)
命題U :
　任意の正数εに対して、あるR²上の点Aの除外δ近傍U*_δ(A)をとると、
　　任意のP,Q∈U*_δ(A)にたいして、|f (P)−f (Q)|＜εが成り立つ。
　論理記号では、
　(∀ε>０) (∃U*_δ(A)) (∀P,Q∈U*_δ(A))) (|f (P)−f (Q)|＜ε)
　　　　

活用例

証明

[命題S⇒ 命題Tの証明]

・2変数関数の収束の定義より、
　　命題S「f ( P )→c (P→A)」⇔「（∀ε/2>０）（∃δ>０）（∀P∈R² ）（０＜d( P, A )＜δ⇒|f (P)−c|＜ε/2 ）」
　　命題S「f ( P )→c (P→A)」⇔「（∀ε/2>０）（∃δ>０）（∀Q∈R² ）（０＜d( Q, A )＜δ⇒|f (Q)−c|＜ε/2 ）」
　したがって、命題S「f ( P )→c (P→A)」が成り立つならば、　　
　（∀ε/2>０）（∃δ>０）（∀P,Q∈R² ）
　　　（０＜d( P, A )＜δかつ０＜d( Q, A )＜δ⇒|f (P)−c|＜ε/2 かつ|f (Q)−c|＜ε/2
　　　　　　　　　　　　　　　　　　　　　　　⇒|f (P)−c|＋|f (Q)−c|＜ε）　…(1)　
・|f (P)−f (Q)|≦| f (P)−c |＋|f (Q)−c |　…(2)　
　なぜなら、　
　　|f (P)−f (Q)|＝| (f (P)−c)+(−f (Q)+c) |
　　　　　　　≦| f (P)−c |＋|−f (Q)+c |　　∵絶対値の三角不等式
　　　　　　　　　　＝| f (P)−c |＋|−(f (Q)−c) |　
　　　　　　　　　　　　＝| f (P)−c |＋|f (Q)−c |　
・(1)(2)をあわせると、
　命題S「f ( P )→c (P→A)」が成り立つならば、　
　（∀ε>０）（∃δ>０）（∀P,Q∈R² ）
　　　　　　　　（０＜d( P, A )＜δかつ０＜d( Q, A )＜δ⇒|f (P)−f (Q)|≦|f (P)−c|＋|f (Q)−c|＜ε）　　　
　となる。

[命題T⇒ 命題Sの証明]

・命題T「(∀ε>０) (∃δ>０)(∀P,Q∈R²) ((０<d (P,A)<δかつ０<d(Q,A)<δ）⇒|f (P)−f (Q)|＜ε)」
　が成り立っていると仮定。　　
・（∀{ P_i }）（（P_i→A (i→∞)かつ(∀i) (P_i ≠A) ）
　　　　　　　　　　　⇔ (∀δ＞０)(∃N∈N)(∀j,k∈N)( j,k≧N⇒０＜d ( P_j , A ) <δかつ０＜d ( P_k , A ) <δ)）
　　　なぜなら、P_i→A (i→∞)の定義が「(∀ε＞０)(∃N∈N)(∀i∈N)( i≧N⇒ d ( P_i , A ) <ε)」で、
　　　　　　　距離の定義より、(∀i) (P_i ≠A)　⇔　(∀i) (０＜d ( P_i , A ) )
　　　となるから。　　　
・したがって、命題Tのもとでは、
　（∀{ P_i }）
　　　（（P_i→A (i→∞)かつ(∀i) (P_i ≠A) ）
　　　　　　⇒(∀ε>０)(∃δ>０)(∃N∈N)(∀j,k∈N)
　　　　　　　　　　( j,k≧N⇒０＜d ( P_j , A ) <δかつ０＜d ( P_k , A ) <δ⇒|f (P_j )−f (P_k )|＜ε)）
　となる。
これは、要するに、
　（∀{P_i }）（（P_i→A (i→∞)かつ(∀i) (P_i ≠A)）⇒((∀ε>０)(∃N∈N)(∀j,k∈N)( j,k≧N⇒|f (P_j )−f (P_k )|＜ε))）
ということ。　
ここで、(∀ε>０)(∃N∈N)(∀j,k∈N)( j,k≧N⇒|f (P_j )−f (P_k )|＜ε)は、
　　　　　　数列 { f (P_i ) } = { f (P₁ ), f (P₂ ), f (P₃ ),… } がコーシー列であることの定義にほかならないから、
命題Tのもとでは、　　
　　（∀{ P_i }）（（P_i→A (i→∞)かつ(∀i) (P_i ≠A) ）⇒数列{f (P_i )}はコーシー列）。
となる。
　コーシーの判定条件「数列{ f (P_i )}はコーシー列⇔数列{f (P_i )}は収束」より、
　命題Tのもとでは、　　
　　　　（∀{ P_i }）（（P_i→A (i→∞)かつ(∀i) (P_i ≠A) ）⇒ 数列{ f (P_i )}）。
　となる。
　さらに、2変数関数の収束を点列･数列の収束に言い換える定理により、　　　
　（∀{ P_i }）（（P_i→A (i→∞)かつ(∀i) (P_i ≠A) ）⇒ f (P_i )は収束）⇔命題S「P→Aのとき、関数f (P)が収束する」　　　　　　
　したがって命題Tが成り立つとの仮定下で、命題Sが成立する。

→[トピック一覧：2変数関数の極限の性質]
→総目次