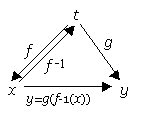1変数関数の導関数の計算公式　：　トピック一覧

定理：定数値関数の微分公式　Constant Function Rule

　・1変数定数値関数y=f (x)= kの導関数は、０。

　・つまり、すべての実数k に対して、　(k)’=０　　

　※なぜ？→証明　

　※逆は成り立つか？→平均値定理の系3　　

	[文献] 　・和達『微分積分』3-3(p.47):証明付;
	・『高等学校基礎解析』p.104

定理：関数の和差の微分公式　Sum-Difference Rule　

　f (x)、g (x)が区間Dで微分可能ならば、

　その和差も区間Dで微分可能であって、

　以下が成り立つ。

　( f (x) ± g (x) )’=f' (x) ± g' (x)　　

　　※なぜ？→証明　 　　　　

	[文献] 　・和達『微分積分』3-3(p.48):証明無 　・矢野・田代『社会科学者のための〜』p.72
	・『高等学校基礎解析』p.105

定理：関数の定数倍の微分公式

　　f (x)が区間Dで微分可能ならば、

　　その定数倍も区間Dで微分可能であって、

　　以下が成り立つ。

　　　( k f (x) )’= k f' (x)　　　（ただし、kは定数）

　　※なぜ？→証明　　　

	[文献] 　・和達『微分積分』3-3(p.48):証明無 　・矢野・田代『社会科学者のための〜』p.72
	・『高等学校基礎解析』p.104

定理：関数の積の微分公式　Product Rule　

　f (x)、g (x)が区間Dで微分可能ならば、

　その積も区間Dで微分可能であって、

　以下が成り立つ。

　　( f (x) g (x) )’=　f' (x) g (x) ＋ f (x) g' (x)　　

　※なぜ？→証明　 　　

	[文献] 　・小平『解析入門I』§3.2a(pp.112-3):証明付 　・吹田新保『理工系の微分積分学』p.38:証明付; 　・和達『微分積分』3-3(p.48);問題3-3-(1)(p.52;219):証明付 　・矢野・田代『社会科学者のための〜』p.72  　・高橋『経済学とファイナンスのための数学』p.49.
	・『高等学校基礎解析』p.49:証明付

定理：関数の商の微分公式　Quotient Rule　

　f (x)、g (x)が区間Dで微分可能ならば、

　g (x)≠0であるようなx∈Dに対して、
　　　　 f (x) / g (x)も区間Dで微分可能となって、

　以下が成り立つ。

　( f (x) / g (x) )’=　{ f' (x) g (x) −f (x) g' (x) } / g ² (x)　　

　※なぜ？→証明　
　　 　　

	[文献] 　・小平『解析入門I』§3.2a(pp.112-3):証明付 　・吹田新保『理工系の微分積分学』p.38:証明付; 　・和達『微分積分』3-3(p.48);問題3-3-(2)(p.52;220)証明付 　・矢野・田代『社会科学者のための〜』p.72  　・高橋『経済学とファイナンスのための数学』p.49.
	・『高等学校基礎解析』p.50:証明付

定理：合成関数の微分公式 chain rule

　y = f (x)がx=x₀で微分可能で、
　z = g ( y )が y₀ = f ( x₀ ) で微分可能ならば、

　合成関数 z=g ( f (x) )は x=x₀ で微分可能となり、
　微分係数はg' ( f ( x₀ ) ) f ' ( x₀ )で与えられる。

　このことは、dz/dx = dz/dy・dy/dx　とかくことができる。

※図解：ここでの想定
　　　
※簡単な適用例：　y=(2x+3)⁵　の微分　　
　　　y=(2x+3)⁵　は、　　　　　
　　　　z=g(y)=y⁵, y =f(x)=2x+3の合成関数z=g ( f (x) )。　
　　　　　g'(y)=5y⁴　、f ' (x)=2　　だから、　　　　　　　　
　　　　z ' =g' ( f ( x ) ) f ' (x)＝5(2x+3)⁴・2＝10(2x+3)⁴　　　
※なぜ？→証明　　
　　 　　

	[文献] 　・小平『解析入門I』§3.2b(pp.113-5):証明付 　・吹田新保『理工系の微分積分学』pp.38-9:証明付; 　・和達『微分積分』3-3(p.48);問題3-4(p.52;220)証明付 　・矢野・田代『社会科学者のための〜』p.82  　・高橋『経済学とファイナンスのための数学』p.53.
	・『高等学校基礎解析』p.53

定理：逆関数の微分公式　inverse function rule　

　y = f (x) が区間Dで連続かつ狭義単調とする。

　f (x) が x=x₀ で微分可能
　かつ
　この点における微分係数f' (x₀) ≠ 0

　とすると、

　逆関数x= f ^-1 (y) は、y₀ = f ( x₀ )で微分可能で、

　微分係数は1／f ' (x₀)＝1／f ' (f ^-1 ( y0 ))で与えられる。

　このことは、dx / dy = １/( dy/dx )　とかくことができる。

※y = f (x)が区間Dで連続かつ狭義単調だとしても、
　点x=x₀において微分係数f ' (x₀) = 0 となって、
　逆関数x = f ^-1 (y) が、y₀ = f ( x₀ )で微分可能でない例 [小平『解析入門I』115-6]
　　　　y = f (x)＝x³：　連続かつ狭義単調増加だが微分係数 f ' (0) = 0 となって、
　　　　逆関数はy= 0で微分可能ではない。
※なぜ？→証明　　　
　　 　　

	[文献] 　・小平『解析入門I』§3.2c(pp.115-6):証明付 　・吹田新保『理工系の微分積分学』p.40:証明付 　・和達『微分積分』3-3(p.49);問題3-5(p.52;220)証明付 　・高橋『経済学とファイナンスのための数学』p.54.