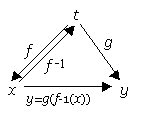→戻る

定理：媒介変数による微分

【文献】吹田新保『理工系の微分積分学』p.40:証明付

　x = f ( t ), y=g( t )において、　　
　　(1)　x = f ( t )は狭義単調
　　(2)　x = f ( t ), y=g( t )がt上の区間Dで微分可能　　
　　(3)　f ' ( t )≠0　
　ならば、　　
　yは xの関数としてx上の区間 f (D)={ x | f －1( x ) ∈D }で微分可能で、
　dy/dx = (dy/dt)/(dx/dt)　

証明

[吹田・新保『理工系の微分積分学』p.40.]
　I.　逆関数t = f －1( x )について。　
　　「(1) x = f ( t )は狭義単調」より、逆関数t = f －1( x )が存在して、これも狭義単調。
　　「(2) x = f ( t )は区間Dで微分可能」ゆえに区間Dで連続　∵連続と微分可能性の関係についての定理　
　　「(3)　f ' ( t )≠0　」　
　　よって、逆関数の微分から、t0∈Dとして、
　　　逆関数t = f －1 ( x )は点x=x0 = f ( t0 )で微分可能…①
　　　また、t = f －1 ( x )の点x=x0 = f ( t0 )での微分係数は1／f ' (t0)。…②　
　II.　 y = g ( f －1 ( x ) )について。　
　　t0∈Dとして、　　　
　　①より、t = f －1 ( x )が x0 = f ( t0 )で微分可能で、
　　「(2) y=g( t )が区間Dで微分可能」よりy=g( t )も t0= f －1 (x0)で微分可能であるので、
　　合成関数の微分についての定理より、
　　　合成関数 y=g( f －1 ( x ) )は x=x0= f ( t0 )で微分可能となり、
　　　x=x0= f ( t0 )での微分係数は g ' (f －1 ( x0 ) ) f －1 ' (x0)で与えられる。
　　②よりf －1 ' (x0)＝1／f ' (t0)、またt0＝f －1 ( x0 )だから、これらを代入すると、　
　　　x=x0= f ( t0 )での微分係数は g ' (t0) ／f ' (t0)　　　　
　　つまり、　　dy/dx = (dy/dt)/(dx/dt)　　　　　　

→戻る