関数y=f(x)は閉区間[a,b] で連 続、
開区間(a,b) で微分可能
(区間の端点では微 分可能でなくてもよい)
ならば、
をみたすcが、
| [文献] ・矢野田代『社会科学者のための基礎数学』p.7 ・赤『実数論講義』§9.3(p.264):実数の連続性 公理の言い換えとして。 ・吹田新保『理工系の微分積分学』pp.44-45 |
||
| ・和達『微分積分』pp.59-60 |
| [文献]
・矢野田代『社会科学者のための基礎数学』pp.76-77 ・赤『実数論講義』§9.3(p.264):実数の連続性公理の言い換えとして。 ・吹田新保『理工系の微分積分学』pp.43-44 ・和達『微分積分』pp.54-55 | ||
|
|
| |
|||
| 【活用例】平均値定理の導出/コーシーの平均値定理の導出/テイラーの定理の導出 | |
||
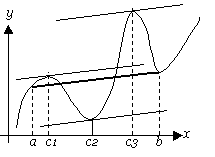
| 【注】証明を見ると分かるように、開区間(a,b)で微分可能でないなら、結論はかわってくる。 |
|||
|
→[トピック一覧: 1変数関数の多項式近似−ロルの定理・平均値定理とその周辺] →総目次 |
| [文献] ・矢野田代『社会科学者のための基礎数学』p.7 ・赤『実数論講義』§9.3(p.264):実数の連続性 公理の言い換えとして。 ・吹田新保『理工系の微分積分学』pp.44-45 |
||
| ・和達『微分積分』pp.59-60 |
| |
|||
| 【活用例】閉区間における広義単調の必要十分条件の導出/閉区間における狭義単調の十分条件の導出/解析学の基本定理の導出 | |
||
| 【関数一般への拡張】2変数関数バージョンの平均値定理/n変数関数バージョンの平均値の定理 【積分バージョン】 積分の第1平均値定理 |
|||
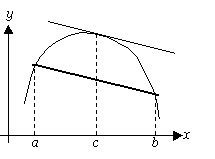
| 【解釈】 [a,b]で連 続、(a,b)で微分可能な関数y=f(x)を 考えると、 区間の両端を結んだ直線と平行な接線ををひける点が、 (a,b)内に少なくと も一つ存在する。 |
|
|
|
→[トピック一覧: 1変数関数の多項式近似−ロルの定理・平均値定理とその周辺] →総目次 |
|
→[トピック一覧: 1変数関数の多項式近似−ロルの定理・平均値定理とその周辺] →総目次 |
| [文献] ・赤『実数論講義』§9.3(p.264):実数の連続性 公理の言い換えとして。 ・小平『解析入門I』p.123 ・高木『解析概論』p.48 ・吹田新保『理工系の微分積分学』p.51 |
||
| ・和達『微分積分』p.62 |
|
→[トピック一覧: 1変数関数の多項式近似−ロルの定理・平均値定理とその周辺] →総目次 |