定理：逆関数の微分公式　inverse function rule　

　y = f (x)　が区間Dで連続かつ狭義単調とする。
　f (x) が　x=x0　で微分可能かつ この点における微分係数　f '(x0) ≠ 0 とすると、
逆関数x = f -1 (y) は、y0 = f ( x0 )で微分可能で、
微分係数は1／f ' (x0)＝1／f ' (f -1 (y0))で与えられる。
このことは、dx / dy = １/( dy/dx )　とかくことができる。
※y = f (x)が区間Dで連続かつ狭義単調だとしても、
　点x=x0において微分係数f ' (x0) = 0 となって、
　逆関数x = f -1 (y) が、y0 = f ( x0 )で微分可能でない例 [小平『解析入門I』115-6]
　　　　y = f (x)＝x3：　連続かつ狭義単調増加だが微分係数f ' (0) = 0 となって、
　　　　逆関数はy= 0で微分可能 ではない。

→戻る　

（証明）

(準備)　
　・仮定：「y = f (x)が区間Dで連続かつ狭義単調」
　　より、　　
　　逆関数x = f -1 (y)は1価連続で狭義単調。　…(1)　　　　∵定理：逆関数の連続性　
　　区間での連続性の定義より、{ y0|f -1 (y0)∈D}で、　　　…(2)　　　
　　ここで、x = f -1 (y), x0= f -1 (y0)（∵(1)）であったから、(2)は以下のように書いても同じ。　　　
　　　　
　　つまり、y→ y0で、x→ x0　　…(3)　
　・仮定：「f (x) がx=x0で微分可能かつ この点における微分係数f ' (x0) ≠ 0」より、
　　　　　　f ' (x0)＝ …(4)　　　

(本題)　
　　逆関数x = f -1 (y) の、y0 = f ( x0 )での微分係数は、
　　　　　　∵微分係数の定義　　
　　　　　　　∵(1)よりx = f -1 (y)、x0 = f -1 (y0)、(3)よりy→ y0のときx→ x 0　
　　　　　　
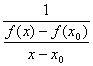
　　　　　＝1／f ' (x0)　　　　　　　∵(4)　　　




　【文献】

　・吹田新保『理工系の微分積分学』p.40.
　・高橋『経済学とファイナンスのための数学』p.54
　・和達『微分積分』p. 52;220.:証明
　・『微分積分』p.57:証明

→戻る