1変数関数の多項式近似2−テイラーの定理：トピック一覧　

テイラーの定理 (入門版―ラグランジュの剰余項)　

・関数f(x) が閉区間[a,b]でn階まで連続な導関数をもち、開区間(a,b)で(n＋1)階微分可能とする。 ・f(b)=f(a)+f ' (a) (b−a) ＋ f '' (a) (b−a)2/(2! )＋…＋ f (n) (a) (b−a)n/ (n! ) ＋ Rn+1　　とおくと、 　・Rn+1=f (n+1) (c) (b−a)n+1 / ( (n+1)! )　を満たすcが、開区間（a, b）内に存在する、（つまり、f (n+1) (c) (b−a)n+1 / ( (n+1)! ) かつa<c<bを満たすcが存在する） 　・ないしは、c を a+θ( b−a )と書いて、（　a<c<b⇔０＜θ＜１だから　） 　　Rn+1=f (n+1) ( a +θ( b−a ) ) (b−a)n+1 /(n+1)!　を満たすθが開区間(0,1)内に存在する。（つまり、Rn+1=f (n+1) ( a +θ( b−a ) ) (b−a)n+1 /(n+1)!　 かつ ０＜θ＜1 を満たすθが存在する） ・この Rn+1 をラグランジュの剰余項 Lagrange form of the remainderと呼ぶ。 ※以下のように書いても全く同じ。 　f(b)=f(a)+f ' (a) (b−a)＋f '' (a) (b−a)2/ (2! )＋…＋f (n-1) (a) (b−a)n-1/(n-1)!＋Rnとおくと、 　　・Rn= f (n) (c) (b−a)n /(n! )を満たすcが、開区間（a, b）内に存在する。（つまり、「Rn= f (n) (c) (b−a)n /(n! ) かつ　a<c<b」を満たすcが存在する） 　　・ないしは、c を a +θ( b−a )と書いて（a<c<b ⇔ ０＜θ＜１ だから） 　　　Rn= f (n) ( a +θ( b−a )) (b−a)n /(n! )　を満たすθが開区間(0,1)内に存在する。　（つまり、Rn= f (n) ( a +θ( b−a ) ) (b−a)n /(n! ) かつ ０＜θ＜１を満たすcが存在する） 　※　f(n) の意味、　n！の意味、Σの意味、　 【解釈】 　　 開区間（a, b）内のどこかに存在するcを用いると、f(b)をこのように「(n項までの級数)＋(cを用いた剰余項)」で表せる！　というのが、メインメッセージ。

コーシーの剰余項の導出　　

 [参照：吹田・新保『理工系の…』p.46.]　　　　　　　cf.ラグランジュの剰余項、テイラーの定理：本格版　

　　関数f(x) が閉区間[a,b]で(n−1)階まで連続な導関数をもち、開区間(a,b)でn階微分可能とする。　
　　　f(b) = f(a) + f ' (a) (b−a) ＋ f '' (a) (b−a)²/2! ＋  … ＋ f ^(n-1) (a) (b−a)^n-1/( (n-1)! )  ＋ R_n　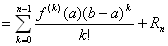　　　　とおくと、
　　　　　R_n= f ⁽ⁿ⁾ (c) (b−c)^n-1 (b−a) /( (n−1)! )　
　　　を満たすcが、開区間（a, b）内に存在する。
　　　　　　（つまり、「 R_n= f ⁽ⁿ⁾ (c) (b−c)^n-1 (b−a) /( (n−1)! ) かつ a<c<b 」を満たすcが存在する）
　　　ないしは、c を a +θ( b−a )と書いて（a<c<b ⇔ ０＜θ＜１ だから）
　　　　　R_n= f ⁽ⁿ⁾ ( a +θ(b−a ) ) (b−a−θ(b−a ))^n−１ (b−a) /( (n−1)! )　
　　　　　　 = f ⁽ⁿ⁾ ( a +θ(b−a ) ) ( (1−θ) (b−a ))^n−１ (b−a) /( (n−1)! )　
　　　　　　 = f ⁽ⁿ⁾ ( a +θ(b−a ) ) (1−θ)^n-1 (b−a )ⁿ /( (n−1)! )　
　　　を満たすθが開区間(0,1)内に存在する。
　　このR_nをコーシーの剰余項 Cauchy form of the remainder と呼ぶ。

　　※　以下のように書いても全く同じ。　
　　　　　　f(b) = f(a) + f ' (a) (b−a) ＋ f '' (a) (b−a)²/2! ＋ … ＋ f ⁽ⁿ⁾ (a) (b−a)ⁿ/ (n! ) ＋R_n+1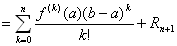　　
　　　　とおくと、
　　　　　　R_n+1= f ⁽ⁿ⁺¹⁾ (c ) (b−c)ⁿ (b−a)/(n! )　
　　　　を満たすcが、開区間（a, b）内に存在する。

　　　　ないしは、c を a +θ( b−a)と書いて、（a<c<b⇔ ０＜θ＜１だから）
　　　　　　R_n+1 = f ⁽ⁿ⁺¹⁾ ( a +θ( b−a ) ) (b−a−θ(b−a ))ⁿ (b−a)/(n! )　
　　　　　　　　= f ⁽ⁿ⁺¹⁾ ( a +θ( b−a ) ) ((1−θ) (b−a ))ⁿ (b−a)/(n! )　
　　　　　　　　= f ⁽ⁿ⁺¹⁾ ( a +θ( b−a ) ) (1−θ)ⁿ (b−a )⁽ⁿ⁺¹⁾/(n! )　
　　　　を満たすθが開区間(0,1)内に存在する。　　

　　※　f⁽ⁿ⁾ の意味、　n！の意味、Σの意味　　

【解釈】　

　開区間（a, b）内のどこかに存在するcを用いると、f(b)をこのように「[n項までの級数]＋[cを用いた剰余項]」で表せる！
　というのが、メインメッセージ。

※なぜ？→証明　

※活用例：　

テイラーの定理(本格版)　

　※テイラーの定理：入門版　　　

　f(x)を区間Iでn階微分可能な関数とする。a∈Iを定点、x∈Iを任意の点とするとき、　

　以下の式を満たす点cがxとaの間に存在する (つまり c = a +θ( x−a ),0＜θ＜1 )。　
　　　f(x) ＝ f(a) + f ' (a) (x−a) /(1!) ＋ f '' (a) (x−a)²/(2!) ＋ … ＋ f ^(n-1) (a) (x−a)^n-1/(n-1)!＋R_n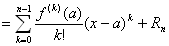　　
　　　　　R_n= f ⁽ⁿ⁾ (c) (x−a)ⁿ /(n!)　
※　f⁽ⁿ⁾ の意味、　n！の意味、Σの意味、　

【ポイント】　

　a＜c＜b として、f(b)を、「aを用いた級数」と「cを用いた剰余項」で表したのが、入門版テイラーの定理だった。　
　それを、a＜c＜xでも、x＜c＜aでも構わなくすると、本格版になる。　　
　したがって、この本格版の証明方法として、
　入門版の定理がaとbを入れ替えても成立することを示すというのも考えられる。　
　　　　　　　[→吹田・新保『理工系の…』p.46.]　　
※なぜ？→証明
※活用例：テイラー展開・マクローリン展開　

様々な剰余項：Schlomilchの剰余項　

テイラーの定理の積分形　　　　　

（reference）