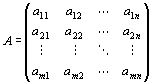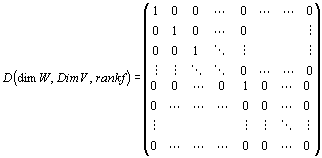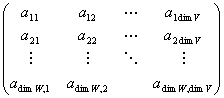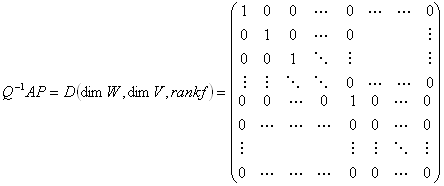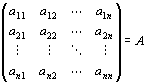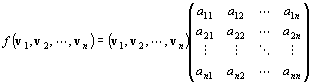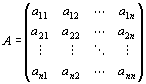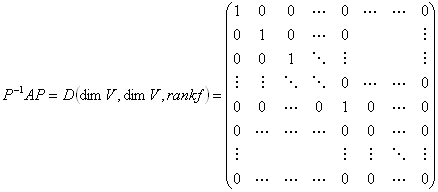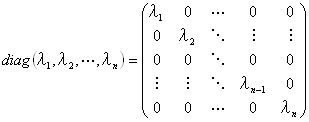定理:一次写像・線形写像の行列表示・行列表現
この定理は、以下の舞台設定上で成り立つ。
V :実ベクトル空間(実数体R上の線形空間・ベクトル空間」)であって、
n次元。つまり、dimV=n
{ v1, v2, …, vn }:Vの基底をなす、Vに属すベクトルの集合
W :実ベクトル空間(実数体R上の線形空間・ベクトル空間」)であって、
m次元。つまり、dimW=m
{ w1, w2, …, wm }:Wの基底をなす、Wに属すベクトルの集合
[
文献]・永田『理系のための線形代数の基礎』定理1.4.1(p.28);
・斎藤『線形代数入門』4章§5(pp.113-4) 本論4で定義して、本論1を定理として導出;
・志賀『線形代数30講』17講(p.109);
・ホフマン・クンツェ『線形代数学I』3.4行列による一次変換の表現(p.89);
・藤原『線形代数』4.3(p.102);
・神谷浦井『経済学のための数学入門』§5.2.1線形写像の行列表現(p.165);
・松坂『解析入門4』15.1-F(p.12);
・砂田『行列と行列式』§5.5(a) (p.187):
体上のベクトル空間のあいだの一次写像全般について。
・酒井『環と体の理論』1.6(p.23)
V
の基底{ v1, v2, …, vn }、Wの基底{ w1, w2, …, wm }と、一次写像「f:V→W」にたいして、
f (v1)=a11w1+a21w2+…+am1wm
f (v2)=a12w1+a22w2+…+am2wm
: :
f (vn)=a1nw1+a2nw2+…+amnwm
を満たす(m,n)型実行列
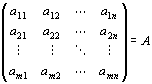
が一意的に存在する。
| f (v1)=a11w1+a21w2+…+am1wm
| f (v2)=a12w1+a22w2+…+am2wm
| : :
| f (vn)=a1nw1+a2nw2+…+amnwm
を、行列の乗法風に、
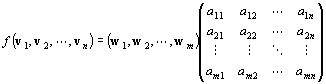
と書く、簡便法が、頻繁に用いられる。
この簡便法を用いると、上記の命題は、次のように、簡潔に表せる。
| Vの基底{ v1, v2, …, vn },Wの基底{ w1, w2, …, wm }と、一次写像f:V→Wにたいして、
| f (v1, v2, …, vn)=(w1, w2, …, wm )A
| を満たす(m,n)型実行列Aが一意的に存在する
※ポイント
「一次写像f : V→W」の行列表示は、
「一次写像f:Rn→Rm」の行列表示の場合とちがって、
V,Wに、標準基底と呼ばれる基底がないので、
自分で自由に基底をV,Wに定めて、
「一次写像f : V→W」を行列表示するほかない。
※ポイント
「一次写像f : V→W」の行列表示は、
Vの基底のとりかた,Wの基底のとりかたの二点から、定まる。
これに対して、
一次変換の行列表示は、Vの基底のとりかたのみから、定まる。
この違いは、
基底を取り替えが、行列表示に及ぼす影響を、
考察する際に、重要になる。
証明
※
なぜ?→証明