実ベクトル空間における一次結合・線形結合 : トピック一覧
・定義:一次結合・線形結合/~から生成された部分ベクトル空間
・定理:一次結合の和/一次結合のスカラー倍/一次結合と部分ベクトル空間
※実ベクトル空間関連ページ:実ベクトル空間の定義/部分ベクトル空間/線形独立・線形従属/基底/次元
※一次写像関連ページ:一次写像-定義/一次写像と演算/一次写像の代数系/一次写像と線形独立/同型写像/同型写像と線形独立
定義:一次結合・線形結合 linear combination
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
+:実ベクトル空間Vにおいて定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:実ベクトル空間Vにおいて定義されているスカラー乗法
v1, v2, …, vl:Vに属すベクトル。つまり、v1, v2, …, vl ∈V 。なお、個数が有限個であることに注意。
【本題】
実ベクトル空間Vに属す有限個のベクトルv1, v2, …, vlの一次結合・線形結合とは、
それらの(Vで定義された)スカラー積 a1v1, a2v2, …, alvl (a1, a2, …, al ∈R)
の(Vで定義された)ベクトル和 a1v1+a2v2+…+alvl 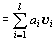
で表されたV上のベクトルのこと。
※「Vに属すベクトルの一次結合」も、「Vに属すベクトル」になるのはなぜ? [草場『線形代数』2.9(p.54)]
【Step1: スカラー積が「Vに属すベクトル」になるわけ】
実ベクトル空間Vにおいて定義されるスカラー乗法とは、
「任意の実数(実数体Rの元)aと、Vの任意の元vの組に対して、Vの元を一意的に定める演算」
のこと。
だから、
任意のai ∈R, vi∈V に対して、Vに定められたスカラー乗法をおこなった結果出てきたスカラー積aiviは、
Vの元 である。
(そもそも、演算結果がVの元にならないなら、その演算はVに定められたスカラー乗法とは呼べない)
Vの元を「Vに属すベクトル」と呼ぶのだから、
任意のai ∈R, vi∈V に対して、Vに定められたスカラー乗法をおこなった結果出てきたスカラー積aiviは、
「Vに属すベクトル」となる。
【Step2: ベクトル和が「Vに属すベクトル」になるわけ】
ベクトル空間Vにおいて定義される"ベクトルの加法"+"とは、
「任意のu,v∈Vに対して、それに対応するu+v∈Vを一つずつ定める」演算のこと。
だから、
任意のu,v∈Vに対して、Vに定められたベクトルの加法をおこなった結果出てきたベクトル和u+vは、
Vの元 である。
(そもそも、演算結果がVの元にならないなら、その演算はVに定められたベクトルの加法とは呼べない)
Vの元を「Vに属すベクトル」と呼ぶのだから、
任意のu,v∈Vに対して、Vに定められたベクトルの加法をおこなった結果出てきたベクトル和u+vは、
「Vに属すベクトル」となる。
【Step3: 一次結合が「Vに属すベクトル」になるわけ 】
step1より、Vに属す任意のベクトルv1, v2, …, vlに対して、
それらの(Vで定義された)スカラー積 a1v1, a2v2, …, alvl (a1, a2, …, al ∈R)
は、すべて、「Vに属すベクトル」となる。
したがって、これらの(Vで定義された)ベクトル和 a1v1+a2v2+…+alvlは、
「Vに属すベクトル」のベクトル和であるから、
step2より、a1v1+a2v2+…+alvlも、「Vに属すベクトル」となる。
つまり、Vに属すベクトルv1, v2, …, vlの一次結合は、「Vに属すベクトル」である。
【文献】
・『岩波数学辞典』210線形空間:C線形結合(p.571)
・斎藤『線形代数入門』4章§3(p.99)
・志賀『線形代数30講』14講(p.90)
・永田『理系のための線形代数の基礎』1.2(p.10);1.3(p.16)
・藤原『線形代数』4.2(p.94)
・ホフマン『線形代数学I』2.1ベクトル空間(p.32)
・神谷浦井『経済学のための数学入門』§3.1.3(p.108);]
定理:一次結合の和
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
+:実ベクトル空間Vにおいて定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:実ベクトル空間Vにおいて定義されているスカラー乗法
v1, v2, …, vl:Vに属すベクトル。つまり、v1, v2, …, vl ∈V 。
a1, a2, …, al :スカラー。a1, a2, …, al ∈R
b1, b2, …, bl :スカラー。b1, b2, …, bl ∈R
【本題】
任意のベクトルv1, v2, …, vl∈Vと、任意のスカラーa1, a2, …, al ,b1, b2, …, bl ∈Rにたいして、
(あるいは、任意の「Vに属すベクトルの一次結合」a1v1+a2v2+…+alvl, b1v1+b2v2+…+blvlにたいして)
(a1v1+a2v2+…+alvl)+(b1v1+b2v2+…+blvl)=(a1+b1)v1+(a2+b2)v2+…+(al+bl)vl
つまり、
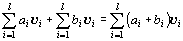
【なぜ?】
(a1v1+a2v2+…+alvl)+(b1v1+b2v2+…+blvl)
=(a1v1+b1v1)+(a2v2+b2v2)+…+(alvl+blvl) ∵ベクトル和の結合則・可換則
=(a1+b1)v1+(a2+b2)v2+…+(al+bl)vl ∵スカラー積のスカラーに関する分配則
【意義】
この定理は、以下の点を意味している。
・「Vに属すベクトル」v1, v2, …, vlの任意の二つの一次結合の「Vで定義されたベクトル和」も、
同じ「Vに属すベクトル」v1, v2, …, vlの一次結合となる。
∵実数体の定義より、実数体の加法"+"は二項演算だから、Kが実数体でai ,bi∈R ならば、ai +bi∈R。
したがって、上記右辺は「Vに属すベクトルの一次結合」の定義を満たす。
【文献】
・ホフマン『線形代数学I』2.1ベクトル空間(p.32)
定理:一次結合のスカラー倍
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
+:実ベクトル空間Vにおいて定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:実ベクトル空間Vにおいて定義されているスカラー乗法
スカラーに続けてスカラーを並べて書いたもの:実数体Rにおいて定義されている乗法
v1, v2, …, vl:V上のベクトル。つまり、v1, v2, …, vl ∈V
c, a1, a2, …, al :スカラー。c, a1, a2, …, al ∈R
【本題】
任意のベクトルv1, v2, …, vl∈Vと、任意のスカラーa1, a2, …, al ,c∈R にたいして、
(あるいは、任意の「Vに属すベクトルの一次結合」a1v1+a2v2+…+alvlと、任意のスカラーc∈R にたいして)
c (a1v1+a2v2+…+alvl)=(ca1)v1+(ca2)v2+…+(cal)vl
つまり、
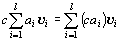
【なぜ?】
c (a1v1+a2v2+…+alvl)
=c {a1v1+(a2v2+…+alvl)} ∵ベクトル和の結合則
=(ca1)v1+c(a2v2+…+alvl) ∵スカラー積のベクトルに関する分配則
=(ca1)v1+c{a2v2+(a3v3+…+alvl)} ∵ベクトル和の結合則
=(ca1)v1+(ca2)v2+ c (a3v3+…+alvl) ∵スカラー積のベクトルに関する分配則
:
:
=(ca1)v1+(ca2)v2+…+(cal)vl
【意義】
この定理が意味しているのは、
「Vに属すベクトル」v1, v2, …, vlの任意の一次結合の、任意の「Vで定義されたスカラー倍」も、
同じ「Vに属すベクトル」v1, v2, …, vlの一次結合となる
ということ。→生成された部分ベクトル空間。
∵実数体の定義より、実数体の乗法は二項演算だから、 c,ai∈Rならば、cai∈R。
したがって、上記右辺は「Vに属すベクトルの一次結合」の定義を満たす。
【文献】
・ホフマン『線形代数学I』2.1ベクトル空間(p.32)
定義:~から生成された部分ベクトル空間、~の線形包 linear hull
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
S:Vの部分集合。つまり、Vに属すベクトルの集合。(Vの部分ベクトル空間である必要はない。また、無限個のベクトルがSに属していてもよい。)
【本題】
1. Sから取り出した任意の有限個のベクトルの任意の一次結合をすべてあつめた集合
〈S〉={ a1v1+a2v2+…+alvl | a1,a2,…,al ∈R, v1,v2,…,vl ∈S⊂V }
は、Sを含む最小の「Vの部分ベクトル空間」となる。(→証明)
2.「Sを含む最小の「Vの部分ベクトル空間」」は、「Sが張る部分空間」《S》と一致するから(→理由)、
上記の〈S〉は、「Sが張る部分空間」《S》と一致する。
3. そこで、Sに属す任意のベクトルの任意の一次結合をすべてあつめた集合〈S〉を、
Vの部分集合Sから生成された部分ベクトル空間、Vの部分集合Sの線形包とよぶ。
【1.の証明】
[永田『理系のための線形代数の基礎』1.5(p.32);砂田『行列と行列式』§5.2補題5.23(p.163); ]
step1: 〈S〉は、Vの部分ベクトル空間。
step1-1: 〈S〉は、Vの部分集合。
Vの部分集合Sから取り出した任意の有限個のベクトルの任意の一次結合を全てあつめた集合〈S〉は、Vの部分集合である。
なぜなら、Vの部分集合Sから取り出した任意の有限個のベクトルは、ベクトル空間Vに属すベクトルだから、
その任意の一次結合は、ベクトル空間Vに属すベクトル。
よって、Vの部分集合Sから取り出した任意の有限個のベクトルの任意の一次結合をすべてあつめた集合〈S〉は、Vの部分集合である。
※Vの部分集合Sに属すベクトルの一次結合は、必ずしもSに属すベクトルとはいえないことに注意。
ここでは、Vはベクトル空間だがSは必ずしもベクトル空間とは設定されていない。
step1-2: 〈S〉は「Vで定義されたベクトルの加法」について閉じている
任意のa1,a2,…,al ∈R, v1,v2,…,vl ∈S⊂V, 任意のa'1,a'2,…,a'm ∈R, v'1,v'2,…,v'm ∈S⊂V に対して、
(a1v1+a2v2+…+alvl)+(a'1v'1+a'2v'2+…+a'mv'm )
=a1v1+a2v2+…+alvl+a'1v'1+a'2v'2+…+a'mv'm ∵ベクトル和の結合則
は、Vの部分集合Sから取り出した任意の有限個のベクトルv1,v2,…,vl ,v'1,v'2,…,v'm の一次結合の定義を満たしている(a1,a2,…,al ,a'1,a'2,…,a'm ∈Rだから)。
つまり、任意の二つの「Vの部分集合Sから取り出した有限個のベクトルの一次結合」の「Vで定義されたベクトル和」は、
「Vの部分集合Sから取り出した有限個のベクトルの一次結合」となる。
ということは、〈S〉に属す任意の二つの元の「Vで定義されたベクトル和」は、〈S〉に属す。
step1-3: 〈S〉は「Vで定義されたスカラー乗法」について閉じている
任意のa1,a2,…,al ∈R, v1,v2,…,vl ∈S⊂V, 任意のc∈R に対して、
一次結合のスカラー倍の定理より、c (a1v1+a2v2+…+alvl)=(ca1)v1+(ca2)v2+…+(cal)vl
つまり、Vの部分集合Sから取り出した任意の有限個のベクトルの任意の一次結合の任意のスカラー倍は、
そのSに属すベクトルの一次結合となる(ca1,ca2,…,cal ∈Rだから)。
ということは、〈S〉に属す任意の二つの元の「Vで定義されたスカラー乗法」は、〈S〉に属す。
step1-4: 以上三点から、〈S〉はVの部分ベクトル空間となるための必要条件を満たす。
Step2: 〈S〉はSを含む。
〈S〉は、Sから取り出した任意の有限個のベクトルの任意の一次結合をすべてあつめた集合であった。
「Sに属す任意のベクトル」自体も、「Sから取り出した任意の有限個のベクトルの任意の一次結合」の一例である。
よって、Sに属す任意のベクトルは、〈S〉に属す。
これを、"⊂"の定義にしたがって、言いなおすと、
S ⊂〈S〉
Step3: 任意の「Sを含む『Vの部分ベクトル空間』」は、〈S〉を含む。
Step3-1:
任意の「Sを含む『Vの部分ベクトル空間』」Wは、
『Vの部分ベクトル空間』であることの必要十分条件より、以下を満たす。
1. Wは、Vの空でない部分集合。
2. 任意のベクトルv1, v2 ∈Wに対して、Vに定められたベクトル和v1+v2 ∈W
3. 任意のベクトルv∈Wとスカラーc∈Rに対して、Vに定められたスカラー積cv∈W
この2.3.の組み合わせと繰り返しによって、
任意のa1,a2,…,al ∈R, 任意のv1, v2,…, vl ∈W⊂Vに対して、
a1v1+a2v2+…+alvl ∈W
となる。
つまり、
Wから取り出した任意の有限個のベクトルv1, v2,…, vl の、Vに定められたベクトル和・スカラー積による一次結合は、Wに属す。
Step3-2:
ここでは、Wとして、任意の「Sを含む『Vの部分ベクトル空間』」を考えているのだから、
S⊂W。
ということは、"⊂"の定義より、 Sに属す元は、すべて、Wにも属す。
だから、
Sから取り出した任意の有限個の元v1,v2,…,vl も、すべて、Wにも属す。
すなわち、v1,v2,…,vl ∈S ⇒v1,v2,…,vl ∈W
この点と、step3-1の結論を合わせて考えると、
任意のa1,a2,…,al ∈R, 任意のv1, v2,…, vl ∈Sに対して、
a1v1+a2v2+…+alvl ∈W
となる。
つまり、 Sから取り出した任意の有限個のベクトルは、 Wから取り出した任意の有限個のベクトルでもあるから、step3-1の結論より、
それら有限個のベクトルの、Vに定められたベクトル和・スカラー積による、任意の一次結合はすべて、Wに属す。
「 Sから取り出した任意の有限個のベクトルの、Vに定められたベクトル和・スカラー積による任意の一次結合」とは、〈S〉の任意の元に他ならないから、
上記は、要するに、〈S〉の任意の元は、Wに属すということ。
これを、"⊃"の定義にしたがって、言いなおすと、
W⊃〈S〉。
Step3-3:
以上から、任意の「Sを含む『Vの部分ベクトル空間』」Wに対して、
W⊃〈S〉。
が成り立つことがわかった。
Step4:
step1,step2の結果より、〈S〉は、「Sを含む『Vの部分ベクトル空間』」の一つであるといえる。
また、step3の結果より、 任意の「Sを含む『Vの部分ベクトル空間』」は、〈S〉を含む。
以上から、〈S〉は、Sを含む最小の「Vの部分ベクトル空間」の定義を満たすことが、明らかになった。
【文献】
・『岩波数学辞典』210線形空間:F部分空間と商空間(p.571)
・永田『理系のための線形代数の基礎』1.5(p.32)
・神谷浦井『経済学のための数学入門』§3.1.4(p.112)
・ホフマン『線形代数学I』2.2部分空間-定理3(p.37)
・砂田『行列と行列式』補題5.23(p.163);]
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、項目210線形空間(pp.570-576)
線形代数のテキスト
ホフマン・クンツェ『線形代数学I』培風館、1976年、2.3基底と次元(pp.41-9)。
志賀浩二『数学30講シリーズ:線形代数30講』朝倉書店、1988年、14講ベクトル空間の例と基本概念(pp.88-90)。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.3ベクトル空間(pp.14-6)。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§6ベクトル空間の公理化(p.115)。
藤原毅夫『理工系の基礎数学2:線形代数』岩波書店、1996年、4.1線形空間と写像(p.91)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第4章§3基底および次元(p.99)。
草場公邦『線形代数(増補版)』(森毅、斉藤雅彦責任編集『すうがくぶっくす』2巻)朝倉書店、1999年。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§3.1ベクトル空間とは何か(p.105)。