一次写像－定義　[数学についてのwebノート]

実線形空間・実ベクトル空間における一次写像の定義

・定義：一次写像･線形写像/像 Image/核Kernel/階数rank/退化次数nullity　　
　　　　一次変換･線形変換･一次作用素･線形作用素/零写像　
・定理：零写像は一次写像　


定義：一次写像・線形写像linear mapping
定義	「実ベクトル空間Vから実ベクトル空間V'への写像f：V→V' が一次写像･線形写像である」とは、　実ベクトル空間Vから実ベクトル空間V'への写像f：V→V' が、　次の二要件を満たすことをいう。　　要件１：写像f：V→V' がベクトル和を保存すること。　　　　　　　つまり、Vの任意のベクトルの(Vで定義された)和の「写像fがV'に写した像」と、　　　　　　　　　　　　それらのベクトルの「写像fがV'に写した像」どおしの(V'で定義された)和とが、　　　　　　　　　一致すること。　　　　　　(∀u,v∈V) ( f ( u+v )=f ( u )+f ( v ) )　　　要件２：写像f：V→V' がスカラー倍を保存すること。　　　　　　　　　つまり、　　　　　「Vの任意のベクトル」の任意の実数(Rの元)による(Vで定義された)スカラー倍を、　　　　　「写像fによってV'に写した像」と、　　　　　　　そのベクトルの「写像fがV'に写した像」の　　　　　任意の実数(Rの元)による(V'で定義された)スカラー倍とが、　　　　　一致すること。　　　　　　(∀v∈V) (∀a∈R) ( f (a v )=a f ( v ) )　　 ※これを、一次変換・線形変換とよぶこともある。[ホフマン『線形代数学I』3.1一次変換(pp.69-76);]	[文献] ・『岩波数学辞典』210線形空間:B線形写像(p.570); ・砂田『行列と行列式』§5.1c定義5.10(p.157)；・永田『理系のための線形代数の基礎』1.3(p.19); ・志賀『線形代数30講』16講(p.100);　・ホフマン『線形代数学I』3.1一次変換(pp.69-76); ・神谷浦井『経済学のための数学入門』§5.2.1(p.163); ・藤原『線形代数』4.1(p.93);] ・松坂『解析入門4』15.1-D (p.7) ※一次写像の諸属性：Image,核Kernel,階数rank,退化次数nullity　 ※具体例：一次変換/射影　 ※実ベクトル空間から実ベクトル空間への線形写像は、　実行列によって表される。（→一次写像の行列表示）　　　だから、線形写像の分類・操作などが論じられる際には、　　　　　それに対応する実行列の分類・操作に思いをめぐらせるのが、　　　　　肝要。
設定	上記の一次写像の定義は、以下の舞台設定上で、なされる。　R：実数体(実数をすべて集めた集合）　　V：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　　　V' ：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　　+：実ベクトル空間Vにおいて定義されているベクトルの加法　　+：実ベクトル空間V'において定義されているベクトルの加法　　スカラーに続けてベクトルを並べて書いたもの：実ベクトル空間Vにおいて定義されているスカラー乗法　　　　　　　　　　　　　　　　　　および、実ベクトル空間V'において定義されているスカラー乗法

→[トピック一覧：一次写像‐定義]
→線形代数目次・総目次


定義：一次写像の像Image
設定	R：実数体(実数をすべて集めた集合）　　 V：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　　 V' ：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　 f：V→V'：実ベクトル空間Vから実ベクトル空間V'への一次写像	[文献] ・砂田『行列と行列式』§5.1c定義5.10(p.157); ・『岩波数学辞典』項目210-F(p.571); ・永田『理系のための線形代数の基礎』1.6 (p.36); ・志賀『線形代数30講』21講(p.133); ・佐武『線形代数学』Ⅲ§4(p.103) ※
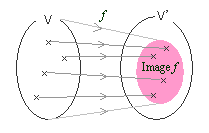
定義	一次写像f：V→V'の像Imageとは、定義域V全体のfによる像　　　　{ f (v ) \| v∈V } のこと。つまり、Vに属すあらゆるベクトルのfによる像をあつめた集合を、fの像と呼ぶ。
記号	一次写像fの像を、Image f , Im f などで表す。
意義	写像f：V→V' という概念は、　定義域V全体のfによる像が、終集合V'と必ずしも一致しなくてもよいものとして定義されていた。（両者が一致する写像は、特に、全射と呼ばれる）一次写像f：V→V'の定義は、写像f：V→V' の概念に、ベクトル和保存・スカラー倍保存の演算則を付け加えただけのものだから、一次写像f：V→V'の定義も、定義域V全体のfによる像が、終集合V'と一致することを要求していない。つまり、一次写像f：V→V'には、定義域V全体のfによる像と終集合V'とが一致しないものが多く含まれている。すると、終集合V'とは別に、定義域V全体のfによる像を検討すべき機会が多々でてくる。そこで「定義域V全体のfによる像」の略称・記号として、「fの像」「Im f 」が用意されることになる。
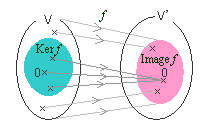
性質	一次写像f：V→V'にたいして、 Image f は、V'の部分ベクトル空間となる。 ※なぜ？→証明　　 ※dim(Image f) を階数と呼ぶ。→詳細
図解

→[トピック一覧：一次写像‐定義]
→線形代数目次・総目次


定義：一次写像の核・核空間　Kernel
設定	R：実数体(実数をすべて集めた集合）　　 V：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　　 V' ：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　 f：V→V'：実ベクトル空間Vから実ベクトル空間V'への一次写像	[文献] ・砂田『行列と行列式』§5.1c定義5.10(p.157); ・ホフマン『線形代数学I』3.1一次変換(p.73); ・『岩波数学辞典』項目210-F(pp.571-2); ・永田『理系のための線形代数の基礎』1.6 (pp.35-6); ・志賀『線形代数30講』21講(p.133); ・佐武『線形代数学』Ⅲ§4(p.103) ※
定義	一次写像f：V→V'の核Kernelとは、fによる像がV'上の零ベクトルとなる「Vに属すベクトル」の集合。つまり、V'上の零ベクトルのfによる逆像　　　f^－1 (０)={ v∈V \| f (v )=０ } のこと。
記号	一次写像fの核を、Ker fで表す。
性質	一次写像f：V→V'にたいして、 Ker f は、Vの部分ベクトル空間である。 ※なぜ？→証明　　 ※dim(Ker f) を退化次数と呼ぶ。→詳細　 ※活用例：一次写像が単射(1対1写像)であるための必要十分条件、
図解	どんな一次写像f：V→V'であれ、V上の零ベクトルを、V'上の零ベクトルに写す。(∵)　だから、どんな一次写像f：V→V'にたいしても、Ker fには必ず、V上の零ベクトルが属す。　もし、一次写像fが、それ以外のV上のベクトルを、V'上の零ベクトルに写すなら、それらのV上のベクトルもすべて、Ker fに属すことになる。

→[トピック一覧：一次写像‐定義]
→線形代数目次・総目次


定義：一次写像の階数　rank
設定	R：実数体(実数をすべて集めた集合）　　 V：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　　 V' ：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　 f：V→V'：実ベクトル空間Vから実ベクトル空間V'への一次写像	[文献] ・『岩波数学辞典』項目210-F(p.572); ・永田『理系のための線形代数の基礎』1.6 (p.37); ・ホフマン『線形代数学I』3.1一次変換(p.73); ・斎藤『線形代数入門』４章§5(p.116); ・佐武『線形代数学』Ⅲ§4(p.105)；・砂田『行列と行列式』§5.5-d定義5.80(p.194). ※
定義	一次写像f：V→V'の階数rankとは、fの像[Image f ]の次元のこと。　　すなわち、rank f = dim(Image f) 　と定義される。
性質	rank f≦dim V'　これは、　 Ker f が「Vの部分ベクトル空間」であること(∵)と、「Vの部分ベクトル空間」の次元は、Vの次元より大きくならないということによる。　　　 ※一次写像の階数の性質、行列の階数

→[トピック一覧：一次写像‐定義]
→線形代数目次・総目次


定義：一次写像の退化次数　nullity
設定	R：実数体(実数をすべて集めた集合）　　 V：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　　 V' ：実ベクトル空間　（実数体R上の線形空間・ベクトル空間」）　 f：V→V'：実ベクトル空間Vから実ベクトル空間V'への一次写像	[文献] ・岩波数学辞典』項目210-F(p.572); ・藤原『線形代数』4.2(p.99); ・志賀『線形代数30講』21講(p.133); ・佐武『線形代数学』Ⅲ§4(p.105:脚注) ※
定義	一次写像f：V→V'の退化次数nullityとは、　　fの核[Ker f ]の次元、すなわち、dim ( Ker f ) 　のこと。
性質	dim ( Ker f ) ≦dim V　これは、　 Ker f が「Vの部分ベクトル空間」であること(∵)と、「Vの部分ベクトル空間」の次元は、Vの次元より大きくならないということによる。

→[トピック一覧：一次写像‐定義]
→線形代数目次・総目次


定義：一次変換・線形変換linear transformation　一次作用素・線形作用素
定義	実ベクトル空間V上の一次変換･線形変換ないしVの一次作用素・線形作用素とは、　実ベクトル空間VからV自身への一次写像f：V→V のことをいう。	[文献] ・『岩波数学辞典』210線形空間:B線形写像(p.570); ・永田『理系のための線形代数の基礎』1.3(p.20); ・ホフマン『線形代数学I』3.2一次変換の代数系(p.78); ・神谷浦井『経済学のための数学入門』§5.3(p.189); ※関連事項：一次変換の行列表示/一次変換の固有値と固有ベクトル
設定	上記の定義は、以下の舞台設定上で、なされる。 R：実数体(実数をすべて集めた集合）　　 V ：実ベクトル空間（実数体R上の線形空間・ベクトル空間」）　 +：実ベクトル空間Vにおいて定義されているベクトルの加法　スカラーに続けてベクトルを並べて書いたもの：実ベクトル空間Vにおいて定義されているスカラー乗法

→[トピック一覧：一次写像‐定義]
→線形代数目次・総目次


定義：零写像
定義	「実ベクトル空間Vから実ベクトル空間V'への写像f：V→V' が零写像である」とは、 Vの任意のベクトルの「写像fがV'に写した像」がすべて、V'の零ベクトルとなることをいう。　　　　　(∀x∈V) (∀a∈R) ( f (x )=〇 )	[文献] ・砂田『行列と行列式』§5.1c定義5.10(p.157)；・松坂『解析入門4』15.1-D (p.7) ※
設定	上記の定義は、以下の舞台設定上で、なされる。 R：実数体(実数をすべて集めた集合）　　 V ：実ベクトル空間（実数体R上の線形空間・ベクトル空間」）。　 V' ：実ベクトル空間（実数体R上の線形空間・ベクトル空間」）。　 +：ベクトル空間Vにおいて定義されているベクトルの加法　 +：ベクトル空間V'において定義されているベクトルの加法　スカラーに続けてベクトルを並べて書いたもの：実ベクトル空間Vにおいて定義されているスカラー乗法　　　　　　　　　　　　　　　　　　　および、実ベクトル空間V'において定義されているスカラー乗法

→[トピック一覧：一次写像‐定義]
→線形代数目次・総目次


定理：零写像は一次写像
定義	ベクトル空間Vからベクトル空間V'への零写像は、一次写像の定義を満たす。	[文献] ・砂田『行列と行列式』§5.1c定義5.10(p.157)；・松坂『解析入門4』15.1-D (p.7) ※
設定	上記の定義は、以下の舞台設定上で、なされる。 R：実数体(実数をすべて集めた集合）　　 V ：実ベクトル空間（実数体R上の線形空間・ベクトル空間」）。　 V' ：実ベクトル空間（実数体R上の線形空間・ベクトル空間」）。　 +：実ベクトル空間Vにおいて定義されているベクトルの加法　 +：ベクトル空間V'において定義されているベクトルの加法　スカラーに続けてベクトルを並べて書いたもの：実ベクトル空間Vにおいて定義されているスカラー乗法　　　　　　　　　　　　　　　　　　　および、ベクトル空間V'において定義されているスカラー乗法

→[トピック一覧：一次写像‐定義]
→線形代数目次・総目次

(reference)
日本数学会編集『岩波数学辞典（第三版）』岩波書店、1985年、項目210線形空間(pp.570-576)
線形代数のテキスト
志賀浩二『数学30講シリーズ：線形代数30講』朝倉書店、1988年、16講線形写像(pp.100-105)。
ホフマン・クンツェ『線形代数学I』培風館、1976年、2.3基底と次元(pp.41-50)。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.3ベクトル空間(pp.14-6)。
砂田利一『現代数学への入門：行列と行列式』2003年、§5.1-c(p.157);§5.5-d(p.194).
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§4一次写像の階数(p.103)。
藤原毅夫『理工系の基礎数学2：線形代数』岩波書店、1996年、4.1線形空間と写像(p.93);4.2線形空間と写像(pp.98-9);
斎藤正彦『線形代数入門』東京大学出版会、1966年、第４章§5線形写像とくに線形変換(pp.113-9)。

数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§5.2.1(p.163);§5.3(p.189).

→[トピック一覧：一次写像‐定義]
→線形代数目次・総目次