Rⁿにおける直交補空間の性質：トピック一覧　　〜　　数学についてのwebノート

　　直交補空間は部分空間、部分空間とその直交補空間への直和分解、Rⁿ上の演算の部分空間と直交補空間への分解
　　直交補空間の直交補空間、直交補空間の包含関係、直交補空間と和空間　　　　

※ユークリッド空間Rⁿにおける直交補空間関連ページ：　　　　
　　　　　　　　　　　　　　　　　直交補空間の定義/直交補空間の基底･次元/直交射影/部分空間の直交　
※実ベクトル空間全般における直交補空間関連ページ：直交補空間の定義/直交補空間の性質/直交射影/部分空間の直交
※ユークリッド空間Rⁿ関連ページ：
　　　ユークリッド空間Rⁿの定義〜内積・ユークリッドノルム・ユークリッド距離/内積の性質/
　　　正規直交系･正規直交基底の定義/直交系・直交基底と内積/直交系･正規直交系の性質/正規直交基底の存在と構成/
　　　計量同型写像/
　　　部分空間の正規直交系･正規直交基底の定義/部分空間における正規直交基底の存在と構成
→線形代数目次・総目次

定理：ユークリッド空間Rⁿの部分空間の直交補空間は、Rⁿの部分空間

舞台
設定

R ：実数体R　　
Rⁿ：実n次元数ベクトル空間　
v₁, v₂：実n次元数ベクトル
　　　具体的に書くと、v₁₁, v₁₂, …, v_1n∈Rとして、v₁=( v₁₁, v₁₂, …, v_1n )∈Ｒⁿ　　
　　　　　　　　　　　v₂₁, v₂₂, …, v_2n∈Rとして、v₂=( v₂₁, v₂₂, …, v_2n )∈Ｒⁿ　　
v₁・v₂：実n次元数ベクトルv₁,v₂の自然な内積。
　　　　　これによって、Ｒⁿは計量実ベクトル空間となる。　
‖v‖：計量実ベクトル空間Rⁿにおけるユークリッドノルム
　　　　　　　　　　　（自然な内積を用いて定義される）　
d (v₁,v₂)：ユークリッドノルムから定められたユークリッド距離　　
（Rⁿ,d）：n次元ユークリッド空間　　
W　：実n次元数ベクトル空間Rⁿの部分ベクトル空間　
W^⊥　：Wの直交補空間　　　　

[文献1]
佐武『線形代数学』�V§3(p.101):証明無;
木村
『線形代数』3.5(p.66);
佐和『回帰分析』2.1.4(p.21):証明無;;

[文献2]
砂田
『行列と行列式』§7.1-(e)補題7.24(p.249):証明付;
志賀
『固有値問題30講』9講(p.71):証明付;
永田
『理系のための線形代数の基礎』4.3(p.119)問1;

本題

実n次元数ベクトル空間Rⁿの部分ベクトル空間Wの直交補空間W^⊥も、　　　　
実n次元数ベクトル空間Rⁿの部分ベクトル空間となる。　　　

証明

実n次元数ベクトル空間Rⁿの部分ベクトル空間Wの直交補空間W^⊥が、　　　　
実n次元数ベクトル空間Rⁿの部分ベクトル空間となることは、
W^⊥が、Rⁿの部分ベクトル空間になるための必要十分条件　
　　Q1：W^⊥は、Ｒⁿの空でない部分集合。論理記号で表すと、W^⊥⊂RⁿかつW^⊥≠φ。
　　Q2：W^⊥は「Ｒⁿに定められているベクトルの加法」について閉じている。
　　　　つまり、W^⊥に属す限りで任意の実n次元数ベクトルu,v に対して、u+v ∈W^⊥　
　　　　　　　　　　論理記号で表すと、（ ∀u,v ∈W^⊥ ）（ u+v ∈W^⊥）。
　　Q3：W^⊥は「Ｒⁿに定められているスカラー乗法」について閉じている。
　　　　W^⊥に属す限りで任意の実n次元数ベクトルvと、任意のスカラーa∈Rに対して、
　　　　　　　av∈W^⊥　　　
　　　　論理記号で表すと、（ ∀v∈W^⊥ ）（∀a∈R ）（ av∈W^⊥ ）。
をすべて満たすことからわかる。
　
[Q1をW^⊥が満たすことの証明]　　
　「Wの直交補空間」W^⊥は、
　　　　　W^⊥={ x∈Rⁿ | すべてのy∈W⊂Rⁿにたいして、x・y=０ }　
　と定義された。
　このように、　「Wの直交補空間」W^⊥とは、
　一定の条件を満たす実n次元数ベクトル空間Rⁿの元、すなわち実n次元数ベクトル
　をあつめたものであるから、
　W^⊥は、Ｒⁿの部分集合であることは明らか。
　また、xを零ベクトルとおくと、
　　　すべてのy∈W⊂Rⁿにたいして、x・y=０　を満たすことから、　
　W^⊥には、少なくとも零ベクトルが属すことがわかる。　
　したがって、W^⊥≠φである。　
　
[Q2をW^⊥が満たすことの証明]　　
　・「Wの直交補空間」W^⊥に属す限りで任意の実n次元数ベクトルu,v は、
　　　　すべてのy∈W⊂Rⁿにたいして、u・y=０、v・y=０ 　…(1)　
　　を満たす。　　　∵直交補空間の定義　　
　・「Wの直交補空間」W^⊥に属す限りで任意の実n次元数ベクトルu,v にたいして、
　　　　(u+v )･y＝u･y＋v･y　　　∵内積の線形性1　
　　　　　　　　　＝０＋０　　　　∵　(1)　
　　　　　　　　　　＝０　　　　
　　したがって、直交補空間の定義より、
　　「Wの直交補空間」W^⊥に属す限りで任意の実n次元数ベクトルu,v のベクトル和　
　　　　　u+v　　
　　も、「Wの直交補空間」W^⊥に属す。　　　
　　
[Q3をW^⊥が満たすことの証明]　　
　・「Wの直交補空間」W^⊥に属す限りで任意の実n次元数ベクトルv は、
　　　　すべてのy∈W⊂Rⁿにたいして、v・y=０ 　…(2)　
　　を満たす。　　　∵直交補空間の定義　　
　・「Wの直交補空間」W^⊥に属す限りで任意の実n次元数ベクトルv と
　　任意のスカラーa∈Rに対して、
　　　　( av )･y＝a ( v )･y　　　∵内積の線形性2　
　　　　　　　　　＝a０　　　　∵　(1)　
　　　　　　　　　　＝０　　　　
　　したがって、直交補空間の定義より、　
　　「Wの直交補空間」W^⊥に属す限りで任意の実n次元数ベクトルv の任意のスカラー倍
　　　　　　　av∈W^⊥　　（a∈R ）　
　　　　も、「Wの直交補空間」W^⊥に属す。

→[トピック一覧：直交補空間の性質]

→線形代数目次・総目次

定理：ユークリッド空間Rⁿは、その部分空間とその直交補空間に直和分解される

舞台
　設定

R ：実数体R　　
Rⁿ：実n次元数ベクトル空間　
v₁, v₂：実n次元数ベクトル
　　　具体的に書くと、v₁₁, v₁₂, …, v_1n∈Rとして、v₁=( v₁₁, v₁₂, …, v_1n )∈Ｒⁿ　　
　　　　　　　　　　　v₂₁, v₂₂, …, v_2n∈Rとして、v₂=( v₂₁, v₂₂, …, v_2n )∈Ｒⁿ　　
v₁・v₂：実n次元数ベクトルv₁,v₂の自然な内積。
　　　　　これによって、Ｒⁿは計量実ベクトル空間となる。　
‖v‖：計量実ベクトル空間Rⁿにおけるユークリッドノルム
　　　　　　　　　　　（自然な内積を用いて定義される）　
d (v₁,v₂)：ユークリッドノルムから定められたユークリッド距離　　
（Rⁿ,d）：n次元ユークリッド空間　　
W　：実n次元数ベクトル空間Rⁿの部分ベクトル空間　
W^⊥　：Wの直交補空間　　　　

[文献1]
佐武
『線形代数学』�V§3定理6(p.101):証明付;p.102;
佐和『回帰分析』
　　2.1.4(p.22-3);
久米『数理統計学』1.9.(p.9)。

[文献2]
砂田
『行列と行列式』§7.1-(e)補題7.25(1)(p.249):証明付;
志賀
『固有値問題30講』
9講(p.71):証明付;
永田
『理系のための線形代数の基礎』
定理4.3.1(p.119);

定理1

実n次元数ベクトル空間Rⁿは、
「Rⁿの部分ベクトル空間」Wと、「Wの直交補空間」W^⊥へ直和分解され、
　　　
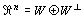
と表せる。　　　

定理2

Wが「実n次元数ベクトル空間Rⁿの部分ベクトル空間」であるならば、　
任意のx∈Rⁿにたいして、
　ある x'∈Wと、ある x''∈W^⊥ が一意に存在して、　　
　　x＝x'＋x''　　　
　　　　　　　*右辺の＋は、実n次元数ベクトル空間Rⁿに定められたベクトル和　
と一意的に表せる。　（直和分解の定義に遡って、定理1を書き下すと、明らか）　　
　　　　

※計量実ベクトル一般において
※活用例：直交射影　　

定理1
証明

Rⁿが、「Rⁿの部分ベクトル空間」Wと、「Wの直交補空間」W^⊥へ直和分解されることを示すには、直和分解の定義より、以下の２点について示せばよい。
(�T) W∩W^⊥={０}　　
(�U) Rⁿは、WとW^⊥との和空間。すなわち、Rⁿ=W＋W^⊥ 。　　
　　　　つまり、任意のx∈Rⁿにたいして、
　　　　　　　　ある x'∈Wと、ある x''∈W^⊥ が存在して、　　
　　　　　　　　x＝x'＋x''　　と表せる。　

[文献]
佐武『線形代数学』�V§3定理6(p.102):証明付
砂田『行列と行列式』

(�T) W∩W^⊥={０}　を示す。　
　　W^⊥とは、Wに属すすべての実n次元数ベクトルと直交する実n次元数ベクトルの集合として定義された。
　　したがって、
　　(W∩W^⊥)に属す実n次元数ベクトル、すなわち、Wに属し、かつ、W^⊥にも属す実n次元数ベクトルは、
　　Wに属す自分自身とも直交しなければならない。
　　ところが、自然な内積の正値性から、自分自身と直交するのは、零ベクトルだけ。
　　したがって、
　　W∩W^⊥={０}　　　
(�U) Rⁿ=W＋W^⊥ 、すなわち、(∀x∈Rⁿ) (∃x'∈W) (∃x''∈W^⊥)（x＝x'＋x''）を示す。
　Step1: 準備
　　Rⁿの任意の部分ベクトル空間には、正規直交基底が存在する（∵）。　　　
　　したがって、「Rⁿの部分ベクトル空間」Wにも正規直交基底が存在する。
　　Wの正規直交基底の一つを、{ v₁ , v₂ , … , v_n }とおく。　
　Step2: 主張　　
　　「 Rⁿ=W＋W^⊥ 」すなわち、(∀x∈Rⁿ) (∃x'∈W) (∃x''∈W^⊥)（x＝x'＋x''）
　　を示すためには、
　　任意のx∈Rⁿにたいしてx＝x'＋x''かつx'∈Wかつx''∈W^⊥を満たすx'、x''の実例を一つあげればよい。　
　　ここでは、
　　任意のx∈Rⁿにたいして、
　　　　　x' ＝ (x･v₁ )v₁＋(x･v₂ )v₂＋…＋(x･v_n )v_n　　　
　　　　　x'' ＝x＋（−x' ）　　
　　とすると、
　　これが、
　　任意のx∈Rⁿにたいしてx＝x'＋x''かつx'∈Wかつx''∈W^⊥を満たすx'、x''の実例となっていることを示す。
　Step3: x'∈Wを示す。　　
　　{ v₁ , v₂ , … , v_n }は、「Wの正規直交基底」であるから、
　　任意のx∈Rⁿにたいして、
　　　　　x' ＝ (x･v₁ )v₁＋(x･v₂ )v₂＋…＋(x･v_n )v_n　　　
　　と定めると、x'∈W　となる。
　　なぜなら、
　　　x･v₁, x･v₂,…, x･v_nは、自然な内積の定義により、スカラー（実数）となるから、
　　　x' ＝ (x･v₁ )v₁＋(x･v₂ )v₂＋…＋(x･v_n )v_n　
　　　は、v₁ , v₂ , … , v_n の一次結合であり、したがって、Wの基底の一次結合。　
　　　基底の定義によって、Wの基底の一次結合は、Wに属す実n次元数ベクトルを表すから、
　　　x' ＝ (x･v₁ )v₁＋(x･v₂ )v₂＋…＋(x･v_n )v_n∈W　
　Step4: x''∈W^⊥を示す。　　
　　任意のx∈Rⁿにたいして、
　　　　　x'' ＝x＋（−x' ）＝x＋（−(x･v₁ )v₁）＋（−(x･v₂ )v₂）＋…＋（−(x･v_n )v_n）　　
　　と定めると、
　　　x''∈W^⊥、つまり、任意のy∈Wに対して、x''･y＝０ となる。
　　なぜなら、
　　1.　{ v₁ , v₂ , … , v_n }は、「Wの基底」であるから、　
　　　　任意のy∈Wは、　v₁ , v₂ , … , v_n の一次結合として表せる。
　　　　　つまり、任意のy∈Wについて、y＝a₁v₁＋a₂v₂＋…＋a_nv_n　（a₁,a₂,…,a_n∈R）　　
　　2.　任意のy∈Wに対して、
　　　　　x''･y＝x''･（a₁v₁＋a₂v₂＋…＋a_nv_n）　　
　　　　　　　　＝x''･（a₁v₁）＋x''･（a₂v₂）＋…＋x''･（a_nv_n）　　∵内積の線形性1　　
　　　　　　　　＝a₁x''･v₁＋a₂x''･v₂＋…＋a_nx''･v_n　　　　　　　　∵内積の線形性2　　
　　　　　　　　＝０　　　　　　　　　　　　　　　　　　　∵x''･v₁＝x''･v₂＝…＝x''･v_n＝０　
　　なお、最後の、　　　　　　　　　　
　　　　x''･v₁＝x''･v₂＝…＝x''･v_n＝０　　　　　
　　は、次のようにして、確かめられる。
　　　x''･v₁＝（x＋（−(x･v₁ )v₁）＋（−(x･v₂ )v₂）＋…＋（−(x･v_n )v_n））･v₁　
　　　　　　＝x･v₁＋（−(x･v₁ )v₁）･v₁＋（−(x･v₂ )v₂）･v₁＋…＋（−(x･v_n )v_n）･v₁　∵内積の線形性1　
　　　　　　＝x･v₁＋（−(x･v₁ )v₁）･v₁＋（−(x･v₂ )v₂）･v₁＋…＋（−(x･v_n )v_n）･v₁　∵逆ベクトルの定義　
　　　　　　＝x･v₁−(x･v₁ )（v₁･v₁）−(x･v₂ )（v₂･v₁）…−(x･v_n )（v_n･v₁）　∵内積の線形性2　　
　　　　　　＝x･v₁−x･v₁ −(x･v₂ )０…−(x･v_n )０　
　　　　　　　　　　　∵{ v₁ , v₂ , … , v_n }は、「Wの正規直交基底」であるから、　　
　　　　　　　　　　　　　　　　　　　v₁･v₁＝1、v₂･v₁＝v₃･v₁＝…＝v_n･v₁＝０　
　　　　　　＝x･v₁−x･v₁ 　
　　　　　　＝０　　　
　　x''･v₂　＝（x＋（−(x･v₁ )v₁）＋（−(x･v₂ )v₂）＋…＋（−(x･v_n )v_n））･v₂　　　
　　　　　　＝x･v₂＋（−(x･v₁ )v₁）･v₂＋（−(x･v₂ )v₂）･v₂＋…＋（−(x･v_n )v_n）･v₂　∵内積の線形性1　
　　　　　　＝x･v₂＋（−(x･v₁ )v₁）･v₂＋（−(x･v₂ )v₂）･v₂＋…＋（−(x･v_n )v_n）･v₂　∵逆ベクトルの定義　
　　　　　　＝x･v₂−(x･v₁ )（v₁･v₂）−(x･v₂ )（v₂･v₂）…−(x･v_n )（v_n･v₂）　∵内積の線形性2　　
　　　　　　＝x･v₂−(x･v₁ )０−(x･v₂ )1−(x･v₃ )０…−(x･v_n )０　　
　　　　　　　　　　　∵{ v₁ , v₂ , … , v_n }は、「Wの正規直交基底」であるから、　　
　　　　　　　　　　　　　　v₂･v₂＝1、v₁･v₂＝v₃･v₂＝v₄･v₂＝……＝v_n･v₂＝０　
　　　　　　＝x･v₂−x･v₂ 　
　　　　　　＝０　　　
　　　　：　
　　　x''･v_n　＝（x＋（−(x･v₁ )v₁）＋（−(x･v₂ )v₂）＋…＋（−(x･v_n )v_n））･v_n　　　
　　　　　　＝x･v_n＋（−(x･v₁ )v₁）･v_n＋（−(x･v₂ )v₂）･v_n＋…＋（−(x･v_n )v_n）･v_n　∵内積の線形性1　
　　　　　　＝x･v_n＋（−(x･v₁ )v₁）･v_n＋（−(x･v₂ )v₂）･v_n＋…＋（−(x･v_n )v_n）･v_n　∵逆ベクトルの定義　
　　　　　　＝x･v_n−(x･v₁ )（v₁･v_n）−(x･v₂ )（v₂･v_n）…−(x･v_n )（v_n･v_n）　∵内積の線形性2　　
　　　　　　＝x･v_n−(x･v₁ )０−(x･v₂ )０…−(x･v_n )1　　
　　　　　　　　　　　∵{ v₁ , v₂ , … , v_n }は、「Wの正規直交基底」であるから、　　
　　　　　　　　　　　　　　v_n･v_n＝1、v₁･v_n＝v₂･v_n＝…＝v_n−１･v_n＝０　
　　　　　　＝x･v_n−x･v_n 　
　　　　　　＝０　　　
　Step5: x＝x'＋x''を示す。　　
　　　x'' ＝x＋（−x' ）　と定めたのだから、明らか。　　
　Step6: 結論　　
　　以上から、
　　任意のx∈Rⁿにたいして、
　　　　　x' ＝ (x･v₁ )v₁＋(x･v₂ )v₂＋…＋(x･v_n )v_n　　　
　　　　　x'' ＝x＋（−x' ）　　
　　とすると、
　　これが、
　　任意のx∈Rⁿにたいしてx＝x'＋x''かつx'∈Wかつx''∈W^⊥を満たすx'、x''の実例となっていることが、
　　明らかになった。 　　　
　　したがって、
　　(∀x∈Rⁿ) (∃x'∈W) (∃x''∈W^⊥)（x＝x'＋x''）　が成立する。
　　つまり、Rⁿ=W＋W^⊥ である。　

→[トピック一覧：直交補空間の性質]

→線形代数目次・総目次

定理：ユークリッド空間Rⁿ上のベクトル和・スカラー乗法・内積は、その部分空間とその直交補空間に分解される

舞台
　設定

R ：実数体R　　
Rⁿ：実n次元数ベクトル空間　
v₁, v₂：実n次元数ベクトル
　　　具体的に書くと、v₁₁, v₁₂, …, v_1n∈Rとして、v₁=( v₁₁, v₁₂, …, v_1n )∈Ｒⁿ　　
　　　　　　　　　　　v₂₁, v₂₂, …, v_2n∈Rとして、v₂=( v₂₁, v₂₂, …, v_2n )∈Ｒⁿ　　
v₁・v₂：実n次元数ベクトルv₁,v₂の自然な内積。
　　　　　これによって、Ｒⁿは計量実ベクトル空間となる。　
‖v‖：計量実ベクトル空間Rⁿにおけるユークリッドノルム
　　　　　　　　　　　（自然な内積を用いて定義される）　
d (v₁,v₂)：ユークリッドノルムから定められたユークリッド距離　　
（Rⁿ,d）：n次元ユークリッド空間　　
W　：実n次元数ベクトル空間Rⁿの部分ベクトル空間　
W^⊥　：Wの直交補空間　　　　

[文献]

佐武
『線形代数学』�V§3(p.102);

定理

Wが「実n次元数ベクトル空間Rⁿの部分ベクトル空間」であるならば、
任意のx,y ∈Rⁿにたいして、
　あるx',y'∈W、 あるx'',y''∈W^⊥ が一意に存在して、
　　x＝x'＋x''　（ x'∈W, x''∈W^⊥ ）　　
　　y＝y'＋y''　（ y'∈W, y''∈W^⊥ ）　　
　　　　　　　*右辺の＋は、実n次元数ベクトル空間Rⁿに定められたベクトル和　
　と一意的に表せて（∵）、　
1. 　x＋y＝（x'＋y'）＋（x''＋y''）　
2. 　cx＝cx'＋cx''　　　
3. 　x･y＝x'･y'＋x''･y''　　　
が成り立つ。　

意義

この定理が意味していること：
　実n次元数ベクトル空間Rⁿに定められた
　　　1. ベクトル和
　　　2. スカラー乗法
　　　3. 内積
　の三演算は、それぞれ、
　Rⁿの部分ベクトル空間におけるベクトル和・スカラー乗法・内積と、
　その直交補空間におけるベクトル和・スカラー乗法・内積との、
　ベクトル和に分解できる。

→[トピック一覧：直交補空間の性質]

→線形代数目次・総目次

定理：ユークリッド空間Rⁿの部分空間の直交補空間の直交補空間は、Rⁿの部分空間

舞台
　設定

R ：実数体R　　
Rⁿ：実n次元数ベクトル空間　
v₁, v₂：実n次元数ベクトル
　　　具体的に書くと、v₁₁, v₁₂, …, v_1n∈Rとして、v₁=( v₁₁, v₁₂, …, v_1n )∈Ｒⁿ　　
　　　　　　　　　　　v₂₁, v₂₂, …, v_2n∈Rとして、v₂=( v₂₁, v₂₂, …, v_2n )∈Ｒⁿ　　
v₁・v₂：実n次元数ベクトルv₁,v₂の自然な内積。
　　　　　これによって、Ｒⁿは計量実ベクトル空間となる。　
‖v‖：計量実ベクトル空間Rⁿにおけるユークリッドノルム
　　　　　　　　　　　（自然な内積を用いて定義される）　
d (v₁,v₂)：ユークリッドノルムから定められたユークリッド距離　　
（Rⁿ,d）：n次元ユークリッド空間　　
W　：実n次元数ベクトル空間Rⁿの部分ベクトル空間　
W^⊥　：Wの直交補空間　　　　

[文献1]
佐武『線形代数学』�V§3例(10)(p.102-3):証明付;
久米『数理統計学』1.9.(p.9)。


[文献2]
砂田『行列と行列式』§7.1-(e)補題7.25(2)(p.250);
永田『理系のための線形代数の基礎』系4.3.2(p.120);
志賀『固有値問題30講』9講(p.71):証明付;

本題

実n次元数ベクトル空間Rⁿの部分ベクトル空間Wの直交補空間の直交補空間（W^⊥)^⊥は、W。　　　

※

計量実ベクトル一般において

証明

佐武『線形代数学』�V§3例(10)(p.102-3);砂田『行列と行列式』　

→[トピック一覧：直交補空間の性質]

→線形代数目次・総目次

定理：直交補空間の包含関係

舞台
　設定

R ：実数体R　　
Rⁿ：実n次元数ベクトル空間　
v₁, v₂：実n次元数ベクトル
　　　具体的に書くと、v₁₁, v₁₂, …, v_1n∈Rとして、v₁=( v₁₁, v₁₂, …, v_1n )∈Ｒⁿ　　
　　　　　　　　　　　v₂₁, v₂₂, …, v_2n∈Rとして、v₂=( v₂₁, v₂₂, …, v_2n )∈Ｒⁿ　　
v₁・v₂：実n次元数ベクトルv₁,v₂の自然な内積。
　　　　　これによって、Ｒⁿは計量実ベクトル空間となる。　
‖v‖：計量実ベクトル空間Rⁿにおけるユークリッドノルム
　　　　　　　　　　　（自然な内積を用いて定義される）　
d (v₁,v₂)：ユークリッドノルムから定められたユークリッド距離　　
（Rⁿ,d）：n次元ユークリッド空間　　
S₁ , S₂　　　：実n次元数ベクトル空間Rⁿの部分ベクトル空間　
S₁^⊥ , S₂^⊥　：S₁ , S₂の直交補空間　　　　

[文献1]


[文献2]
砂田『行列と行列式』§7.1-(e)問8(p.250);
永田『理系のための線形代数の基礎』4.3(p.119)問1;

本題

　　S₁ ⊂ S₂　⇒　S₂^⊥⊂S₁^⊥ 　　　　

※

計量実ベクトル一般において

→[トピック一覧：直交補空間の性質]

→線形代数目次・総目次

定理：ユークリッド空間Rⁿの直交補空間と和空間

舞台
　設定

R ：実数体R　　
Rⁿ：実n次元数ベクトル空間　
v₁, v₂：実n次元数ベクトル
　　　具体的に書くと、v₁₁, v₁₂, …, v_1n∈Rとして、v₁=( v₁₁, v₁₂, …, v_1n )∈Ｒⁿ　　
　　　　　　　　　　　v₂₁, v₂₂, …, v_2n∈Rとして、v₂=( v₂₁, v₂₂, …, v_2n )∈Ｒⁿ　　
v₁・v₂：実n次元数ベクトルv₁,v₂の自然な内積。
　　　　　これによって、Ｒⁿは計量実ベクトル空間となる。　
‖v‖：計量実ベクトル空間Rⁿにおけるユークリッドノルム
　　　　　　　　　　　（自然な内積を用いて定義される）　
d (v₁,v₂)：ユークリッドノルムから定められたユークリッド距離　　
（Rⁿ,d）：n次元ユークリッド空間　　
S₁ , S₂　：実n次元数ベクトル空間Rⁿの部分ベクトル空間　
S₁ ＋ S₂　　：実n次元数ベクトル空間Rⁿの部分空間S₁ , S₂の和空間　
S₁^⊥ , S₂^⊥　：S₁ , S₂の直交補空間　　　　

[文献1]
佐武『線形代数学』�V§3例(11)(12)(p.102-3);
柳井竹内
『射影行列･一般逆行列･特異値分解』§1.2（1.43）(p.8);
[文献2]
砂田
『行列と行列式』§7.1-(e)問8(p.250);

本題

　・　( S₁ ＋ S₂ )^⊥ = S₁^⊥ ∩ S₂^⊥ 　　
　・　( S₁ ∩ S₂ )^⊥ = S₁^⊥ ＋ S₂^⊥ 　　　　　　　　

※

計量実ベクトル一般において

→[トピック一覧：直交補空間の性質]

→線形代数目次・総目次