部分ベクトル空間の和・直和分解・補空間 : トピック一覧
・定義:和空間・和、2つの部分ベクトル空間の直和/補部分空間・補空間/直和分解,
多数の部分ベクトル空間の直和/直和分解
・定理:2つの部分ベクトル空間への直和分解の必要十分条件/多数の部分ベクトル空間への直和分解の必要十分条件
※関連ページ
部分ベクトル空間:定義、部分ベクトル空間の性質、~が張る部分空間、部分空間の次元、直和が定める射影
実ベクトル空間:実ベクトル空間の定義、一次結合、線形従属・線形独立、基
底、次元
定義:部分ベクトル空間の和空間・和 sum
[『岩波数学辞典』210線形空間:F部分空間と商空間(p.571);永田『理系のための線形代数の基礎』1.5(p.33);
砂田『行列と行列式』§5.2-a(p.160)]
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
W1:Vの部分ベクトル空間
W2:Vの部分ベクトル空間
【定義】
実ベクトル空間Vの部分ベクトル空間W1,W2の和空間・和とは、
「W1に属すベクトル」と「W2に属すベクトル」とのベクトル和をすべて集めた集合
{ v1 +v2 | v1 ∈W1 かつ v2 ∈W2 }
のこと。
【記号】
Vの部分ベクトル空間W1,W2の和空間・和を、W1+W2で表す。
※以上の定義により、
実ベクトル空間Vの部分ベクトル空間W1,W2の和空間W1+W2に属す任意のベクトルは、
Vの部分ベクトル空間W1,W2のベクトル和として表せる
ことになる。
定理:部分ベクトル空間の和空間の性質
[永田『理系のための線形代数の基礎』1.5(p.33);砂田『行列と行列式』§5.2-a(p.162)]
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
W1:Vの部分ベクトル空間
W2:Vの部分ベクトル空間
【本題】
1. 実ベクトル空間Vの部分ベクトル空間W1,W2の和空間(W1+W2)もまた、Vの部分ベクトル空間。
2.実ベクトル空間Vの部分ベクトル空間W1,W2の和空間(W1+W2)は、
(W1∪W2)を含む最小の『Vの部分ベクトル空間』。
定義:2つの部分空間の直和、補部分空間・補空間、直和分解
direct sum, complementary subspace, direct sum decomposition
[『岩波数学辞典』210線形空間:F部分空間と商空間(p.571);砂田『行列と行列式』§5.2-b(p.165);
神谷浦井『経済学のための数学入門』§3.1.2(p.106);永田『理系のための線形代数の基礎』1.5(p.34);
柳井竹内『射影行列・一般逆行列・特異値分解』 §1.2(pp.8-9):実n次元数ベクトル空間のみ。 ]
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
W1:Vの部分ベクトル空間
W2:Vの部分ベクトル空間
【和空間の概念を前提した定義】
「実ベクトル空間Vが、その部分ベクトル空間W1,W2の直和direct sumに分解される」
「Vの部分ベクトル空間W2は、Vの部分ベクトル空間W1の補部分空間・補空間complementary subspace 」
「Vの部分ベクトル空間W1は、Vの部分ベクトル空間W2の補部分空間・補空間complementary subspace 」
とは、
V=W1+W2 かつ W1∩W2={0}
が満たされることをいい、
記号
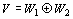
で表す。
また、このかたちで実ベクトル空間Vを表すことを、Vの直和分解direct sum decompositionという。
【和空間の意味に遡る定義】
「実ベクトル空間Vが、その部分ベクトル空間W1,W2の直和direct sumに分解される」
「Vの部分ベクトル空間W2は、Vの部分ベクトル空間W1の補部分空間・補空間complementary subspace 」
「Vの部分ベクトル空間W1は、Vの部分ベクトル空間W2の補部分空間・補空間complementary subspace 」
とは、
・Vが、「W1に属すベクトル」と「W2に属すベクトル」とのベクトル和をすべて集めた集合として表せ、
かつ
・Vの部分ベクトル空間W1,W2の共通部分が0に限られている
ということ、
すなわち、
V={ v1 +v2 | v1 ∈W1 かつ v2 ∈W2 } かつ W1∩W2={0}
が満たされること、
ないしは、
・実ベクトル空間Vに属す任意のベクトルが、Vの部分ベクトル空間W1,W2のベクトル和として表せ、
かつ
・Vの部分ベクトル空間W1,W2の共通部分が0に限られている
ということ
といってもよい。
※実ベクトル空間Vと、Vの部分ベクトル空間W1にたいして、W1の補空間は一意的に定まるわけではない。
W1の補空間は、複数とりうる。[例:砂田『行列と行列式』§5.2-b(p.165);]
定理:直和分解の必要十分条件
[砂田『行列と行列式』補題5.27(p.165):証明付;永田『理系のための線形代数の基礎』定理1.5.5(p.34):証明付;]
実ベクトル空間Vが、Vの部分ベクトル空間W1、W2に直和分解されるということ
つまり、
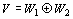
であることの必要十分条件は、
実ベクトル空間Vに属す任意のベクトルが、
「Vの部分ベクトル空間W1に属すベクトル」と「Vの部分ベクトル空間W2に属すベクトル」のベクトル和として、一意的に表せること、
つまり、
実ベクトル空間Vと、Vの部分ベクトル空間W1、W2が与えられているとして、
任意のベクトルv∈Vにたいして、あるベクトルv1∈W1, v2∈W2が一意的に存在して、
v=v1 +v2
と表せるということ。
定義:多数の部分空間の直和、補部分空間・補空間、直和分解
direct sum, complementary subspace, direct sum decomposition
[砂田『行列と行列式』§5.2-b(p.165);永田『理系のための線形代数の基礎』1.5(p.34);
神谷浦井『経済学のための数学入門』§3.1.2(p.107);]
【舞台設定】
R:実数体(実数をすべて集めた集合)
V:実ベクトル空間 (実数体R上の線形空間・ベクトル空間」)
W1,W2,…,Wk:Vの部分ベクトル空間
【定義】
「実ベクトル空間Vが、その部分ベクトル空間W1,W2,…,Wnの直和direct sumに分解される」とは、
V=W1+W2+…+Wn
かつ W1∩(W2+…+Wn)={0}
かつ W2∩(W1+W3+…+Wn)={0}
かつ W3∩(W1+W2+W4+…+Wn)={0}
かつ W4∩(W1+W2+W3+W5+…+Wn)={0}
:
かつ Wk∩(W1+…+Wk-1+Wk+1+…+Wn)={0}
:
かつ Wn∩(W1+…+Wn-1)={0}
が満たされることをいい、
記号
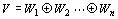
で表す。
また、このかたちで実ベクトル空間Vを表すことを、Vの直和分解direct sum decompositionという。
定理:直和分解の必要十分条件
[砂田『行列と行列式』補題5.30(p.166):証明付;永田『理系のための線形代数の基礎』1.5(e)(p.35);]
実ベクトル空間Vが、Vの部分ベクトル空間W1,W2,…,Wnに直和分解されるということ
つまり、
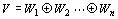
であることの必要十分条件は、
実ベクトル空間Vに属す任意のベクトルが、
「Vの部分ベクトル空間W1に属すベクトル」と
「Vの部分ベクトル空間W2に属すベクトル」と
:
「Vの部分ベクトル空間Wnに属すベクトル」と
のベクトル和として、
一意的に表せること。
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、項目210線形空間(pp.570-576)
線形代数のテキスト
ホフマン・クンツェ『線形代数学I』培風館、1976年、2.1ベクトル空間(pp.28-34)。
砂田利一『現代数学への入門:行列と行列式』2003年、§5.2(p.162).§5.3(p.162).
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.3ベクトル空間(pp.14-6)。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§6ベクトル空間の公理化(p.115)。
志賀浩二『数学30講シリーズ:線形代数30講』朝倉書店、1988年、13講ベクトル空間へ(pp.85-7);14講ベクトル空間の例と基本概念(pp.88-90)。
藤原毅夫『理工系の基礎数学2:線形代数』岩波書店、1996年、4.1線形空間と写像(p.91)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第4章§2線形空間(p.96):実線形空間・複素線形空間のみ;附録Ⅲ§2体(p.249)。
柳井晴夫・竹内啓『UP応用数学選書10:射影行列・一般逆行列・特異値分解』 東京大学出版会、1983年、§1.2ベクトル空間と部分空間(pp.8-9):実n次元数ベクトル空間のみ。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§3.1ベクトル空間とは何か(p.105)。