自然な内積の性質 : トピック一覧・定理:零ベクトルとの内積/スカラー倍したベクトルのそれ自身との内積 |
【関連ページ】 ※計量実ベクトル空間Rn関連ページ:ノルム・ノルム空間の定義/内積・計量実ベクトル空間の定義 ※ユークリッド空間Rn関連ページ:ユークリッド空間Rn-内積・ノルム・距離/内積の性質/正規直交系・正規直交基底の定義/直交系・直交基底と内積/直交系・正規直交系の性質/正規直交基底の存在と構成/計量同型写像 ※ユークリッド空間Rnの部分空間関連ページ:ユークリッド空間の部分空間の基底/ユークリッド空間の部分空間の正規直交基底の存在/直交補空間/直交射影/部分空間の直交 ※上位概念:一般の計量実ベクトル空間と内積 |
|
→線形代数目次 →総目次 |
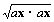
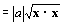
|
→ トピック一覧:Rnにおける自然な内積の性質 → 線形代数目次 → 総目次 |
|
→ トピック一覧:Rnにおける自然な内積の性質 → 線形代数目次 → 総目次 |
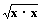

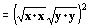
|
→ トピック一覧:Rnにおける自然な内積の性質 → 線形代数目次 → 総目次 |
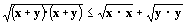

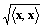
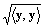 +y・y ∵シュヴァルツの不等式
+y・y ∵シュヴァルツの不等式 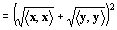
|
→ トピック一覧:Rnにおけ る自然な内積の性質 → 線形代数目次 → 総目次 |
|