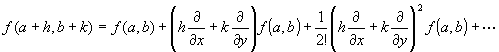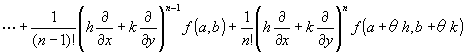|
|
|
|
定理:2変数関数の平均値の定理(1階のテイラーの定理)
|
|
[文献]
・和達『微分積分』p.125;
※対照せよ→1変数関数の平均値定理: f(a+h)=f (a)+h f ' (a +θh) ( 0 <θ< 1 )
→n変数関数の平均値定理(1階のテイラー定理)
※なぜ?→証明
|
| 行列・ベクトル・Σを用いない表現 |
|
2変数関数f(x,y)が微分可能ならば、
f(a+h,b+k)=f(a, b)+h fx(a +θh, b +θk)+k fy(a +θh, b +θk)
を満たすθが 、0 <θ< 1 の範囲に存在する。
h fx(a +θh, b +θk)+k fy(a +θh, b +θk)
を剰余項と呼ぶ。
|
| Σの表現 |
|
|
2変数関数f(x1,x2)が微分可能ならば、
f(a1+h1,a2+h2)=f(a1,a2)+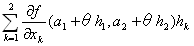
を満たす実数θ∈(0,1)が存在する。
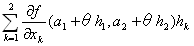
を、剰余項と呼ぶ。
|
|
| ベクトル表現 |
|
|
設定
|
x,a,h:実2次元数ベクトル
つまり、x=(x1, x2)
a=(a1, a2)
h=(h1, h2)
f : 2変数実数値関数
つまり、f :R2⊃D→R
grad f (~) : ~におけるfの勾配ベクトル
|
[文献]
・神谷浦井『経済学のための数学入門』6.3.4定理6.3.4(p.232).1次の項・二次の項までの展開
|
|
本題
|
(表現1)
2変数関数f が微分可能ならば、
f(a+h)= f (a) + grad f(a+θh) ・h
を満たす実数θ∈(0,1)が存在する。
* * * * * * *
grad f(a+θh) ・h
を、剰余項と呼ぶ。
(表現2)
2変数関数f が微分可能ならば、
f(x)= f (a) + grad f(a+θ(x-a)) ・(x-a)
を満たす実数θ∈(0,1)が存在する。
* * * * * * *
grad f(a+θ(x-a)) ・(x-a) を剰余項と呼ぶ。
|
|
→[トピック一覧:2変数関数の平均値の定理・テイラーの定理]
→総目次
(証明:2変数関数の平均値の定理)
Step0:
全微分可能な2変数関数f(x,y)と、
g1(t)= a+ ht、g2(t)= b+ kt (a,h,b,k :定数)との
合成関数 f(g1(t), g2(t)) = f(a+ ht, b+ kt) を、
tの一変数関数とみて、F(t) とおく。
すなわち、
F(t)= f(g1(t), g2(t)) = f(a+ ht, b+ kt)…①
Step1:
F(t)は1変数関数だから、1変数関数の平均値定理より、
F(t+Δt)=F (t)+Δt F ' (t +θΔt)
を満たすθが 0 < θ < 1 の範囲に存在する。
t =0,Δt =1としても、これは成り立つので、
F(0+1)= F (0)+1・F ' (0 +θ・1) を満たすθが 0 < θ < 1 の範囲に存在する
すなわち、
F(1)= F (0)+ F ' (θ) を満たすθが 0 < θ < 1 の範囲に存在する …②
Step2: ②式のうち、F(1),F(0)の計算。
①より、F(1)= f(a+ h・1, b+k・1) = f(a+h, b+k) …③
①より、F(0)= f(a+ h・0, b+k・0) = f(a, b) …④
Step3: ②式のうち、F ' (θ)の計算。
F(t)は合成関数だから(①より)、
合成関数の微分公式を適用して、F(t)の導関数を求めると、
F'(t)=fx ( g1(t), g2(t) ) g1' ( t )+ fy (g1(t), g2(t) ) g2' (t)
= fx( a+ ht , b+ kt ) h+ fy ( a+ ht , b+ kt ) k ∵g1(t)= a+ ht、g2(t)= b+ kt
= h fx ( a+ ht , b+ kt ) + k fy ( a+ ht , b+ kt )
ゆえに、F'(θ)= h fx ( a+ hθ, b+ kθ) + k fy ( a+ hθ , b+ kθ) …⑤
Step4:
③④⑤を②へ代入すれば、②は以下のように言いかえられる。
f(a+h, b+k)= f(a, b)+ h fx ( a+ hθ, b+ kθ) + k fy ( a+ hθ , b+ kθ)
を満たすθが 0 < θ < 1 の範囲に存在する
|
|
|
|
|
定理:2変数関数の2階のテイラーの定理・1次近似多項式
|
|
→[行列・ベクトル・Σを使わない表現/Σの表現/ベクトル行列表現/2次形式] |
[文献]
・岡田『経済学・経営学のための数学』3.2定理3.2
※2変数関数の1階のテイラー定理/3階のテイラー定理
※n変数関数の2階のテイラーの定理
※活用例:極値問題―2階十分条件
|
| 行列・ベクトル・Σを用いない表現 |
設定
|
2変数関数y=f(x,y)をC2級とする。
|
|
本題
|
f(a+h,b+k)= f(a,b)+h fx(a,b)+k fy(a,b)+(1/2) {h2 fxx(a +θh, b+θk) + 2hk fxy(a +θh, b+θk) + k2 fyy(a +θh, b+θk)}
を満たす実数θ∈(0,1)が存在する。
* * * * * * *
上記等式中の
f(a,b)+h fx(a,b)+k fy(a,b)
を、
「(a,b)におけるfの1次の近似多項式」
「(a,b)におけるfの1次のテイラー多項式」と呼ぶ。
また、
(1/2) {h2 fxx(a +θh, b+θk) + 2hk fxy(a +θh, b+θk) + k2 fyy(a +θh, b+θk)}
を、その剰余項と呼ぶ。
[→2階のテイラーの定理冒頭]
|
| Σの表現 |
[文献]
・松坂『解析入門3』14.2-C-定理2(p.155):一般;14.3-C(pp.167-171):ヘッセ行列が定める二次形式を用いた表現。
・高橋『微分と積分2』定理4.7(p.97)。
・杉浦『解析入門』定理7.2(p.147):一般
・黒田『微分積分学』8.6 (p.306):2次の項までのテイラー展開の表現。勾配ベクトル・ヘッセ行列が定める二次形式の活用。
・神谷浦井『経済学のための数学入門』6.3.4定理6.3.4(p.232).1次の項・二次の項までの展開。括弧の前の上についている記号は、転置記号。
・岡田『経済学・経営学のための数学』3.2定理3.2(p.120)
|
|
設定
|
2変数関数y=f(x1,x2)をC2級とする。 |
|
本題
|
f(a1+h1,a2+h2)= f(a1,a2)+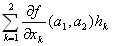
+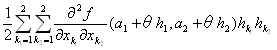
を満たす実数θ∈(0,1)が存在する。
* * * * * * *
上記等式中の
f(a1,a2)+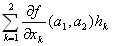
を、
「(a1,a2)におけるfの1次の近似多項式」
「(a1,a2)におけるfの1次のテイラー多項式」と呼ぶ。
また、
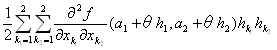
を、その剰余項と呼ぶ。
[→2階のテイラーの定理冒頭]
|
| ベクトル・行列表現 |
|
設定
|
x,a,h:実2次元数ベクトル
つまり、x=t(x1, x2)
a=t(a1, a2)
h=t(h1, h2)
f : 2変数実数値関数
つまり、f :R2⊃D→R
grad f (~) : ~におけるfの勾配ベクトル
Hf(~) :~におけるfのヘッセ行列
|
|
本題
|
2変数関数y=f(x1,x2)がC2級ならば、
f(a+h)= f (a) + grad f(a) ・h+ (1/2) th Hf(a+θh)h
を満たす実数θ∈(0,1)が存在する。
* * * * * * *
上記等式中の
f(a+h)= f (a) + grad f(a) ・h
を、
「aにおけるfの1次の近似多項式」
「aにおけるfの1次のテイラー多項式」と呼ぶ。
また、
(1/2) th Hf(a+θh)h
を、その剰余項と呼ぶ。
[→2階のテイラーの定理冒頭]
|
| ベクトル・行列・2次形式を用いた表現 |
|
設定
|
x,a,h:実2次元数ベクトル
つまり、x=t(x1, x2)
a=t(a1, a2)
h=t(h1, h2)
f :2変数実数値関数。つまり、「f :R2⊃D→R」
grad f (~) : ~におけるfの勾配ベクトル
Hf(~) :~におけるfのヘッセ行列
Hf(~) [h] :「~におけるfのヘッセ行列」によって定まる
h=t(h1, h2)についての二次形式
|
|
本題
|
2変数関数y=f(x1,x2)がC2級ならば、
f(a+h)= f (a) + grad f(a) h + (1/2) Hf(a+θh) [h]
を満たす実数θ∈(0,1)が存在する。
* * * * * * *
上記等式中の
f (a) + grad f(a) h
を、
「aにおけるfの1次の近似多項式」
「aにおけるfの1次のテイラー多項式」と呼ぶ。
また、
(1/2) Hf(a+θh) [h]
を、その剰余項と呼ぶ。
[→2階のテイラーの定理冒頭]
|
|
|
|
定理:2変数関数の3階のテイラーの定理・2次近似多項式
|
|
→[行列・ベクトル・Σを使わない表現/Σの表現/ベクトル行列表現/2次形式] |
|
| 行列・ベクトル・Σを用いない表現 |
|
設定
|
2変数関数y=f(x,y)をC3級とする。
|
|
本題
|
f(a+h,b+k)= f(a,b)+h fx(a,b)+k fy(a,b)+(1/2){h2 fxx(a,b) + 2hk fxy(a,b) + k2 fyy(a,b)}+(1/6){h3 fxxx(a +θh,b+θk)+3h2k fxxy(a +θh,b+θk)+3hk2 fxyy(a +θh,b+θk)+k3 fyyy(a +θh,b+θk) }
を満たす実数θ∈(0,1)が存在する。
* * * * * * *
上記等式中の
f(a+h,b+k)= f(a,b)+h fx(a,b)+k fy(a,b)+(1/2){h2 fxx(a,b) + 2hk fxy(a,b) + k2 fyy(a,b)}
を、「(a,b)におけるfの2次近似多項式」「(a,b)におけるfの2次のテイラー多項式」と呼ぶ。
また、
(1/6){h3 fxxx(a +θh,b+θk)+3h2k fxxy(a +θh,b+θk)+3hk2 fxyy(a +θh,b+θk)+k3 fyyy(a +θh,b+θk) }
を、その剰余項と呼ぶ。
[→3階のテイラー定理冒頭]
|
| Σの表現
|
[文献]
・松坂『解析入門3』14.2-C-定理2(p.155):一般;14.3-C(pp.167-171):ヘッセ行列が定める二次形式を用いた表現。
・高橋『微分と積分2』定理4.7(p.97)。
・杉浦『解析入門』定理7.2(p.147):一般
・黒田『微分積分学』8.6 (p.306):2次の項までのテイラー展開の表現。勾配ベクトル・ヘッセ行列が定める二次形式の活用。
・神谷浦井『経済学のための数学入門』6.3.4定理6.3.4(p.232).1次の項・二次の項までの展開。括弧の前の上についている記号は、転置記号。
・岡田『経済学・経営学のための数学』3.2定理3.2(p.120)
|
|
設定
|
2変数関数y=f(x1,x2)をC2級とする。 |
| 本題 |
f(a1+h1,a2+h2)= f(a1,a2)+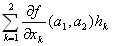 + +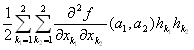
+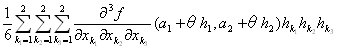
を満たす実数θ∈(0,1)が存在する。
* * * * * * *
上記等式中の
f(a1+h1,a2+h2)= f(a1,a2)+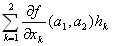 + +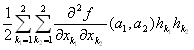
を、「(a1,a2)におけるfの2次の近似多項式」「(a1,a2)におけるfの2次のテイラー多項式」と呼ぶ。
また、
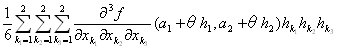
を、その剰余項と呼ぶ。
[→3階のテイラー定理冒頭]
|
| ベクトル・行列表現 |
|
設定
|
x,a,h :実n次元数ベクトル(縦ベクトル)
つまり、x=t(x1, x2)
a=t(a1, a2)
h=t(h1, h2)
f : 2変数実数値関数
つまり、f :R2⊃D→R
grad f (~) : ~におけるfの勾配ベクトル
Hf(~) :~におけるfのヘッセ行列
|
| 本題 |
f(a+h)= f(a) + grad f(a) ・h+ (1/2) th Hf(a)h + 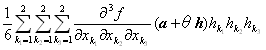
を満たす実数θ∈(0,1)が存在する。
* * * * * * *
上記等式中の
f(a) + grad f(a) ・h+ (1/2) th Hf(a)h
を、「aにおけるfの2次の近似多項式」「aにおけるfの2次のテイラー多項式」と呼ぶ。
また、
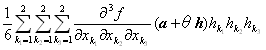
を、その剰余項と呼ぶ。
[→3階のテイラー定理冒頭] |
| ベクトル・行列・2次形式を用いた表現 |
|
|
設定
|
x,a,h:実2次元数ベクトル
つまり、x=t(x1, x2)
a=t(a1, a2)
h=t(h1, h2)
f :2変数実数値関数。つまり、「f :R2⊃D→R」
grad f (~) : ~におけるfの勾配ベクトル
Hf(~) :~におけるfのヘッセ行列
Hf(~) [h] :「~におけるfのヘッセ行列」によって定まる
h=t(h1, h2)についての二次形式
|
|
| 本題 |
f(a+h)= f(a) + grad f(a) ・h+ (1/2) Hf(a) [h] + 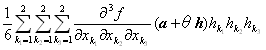
を満たす実数θ∈(0,1)が存在する。
* * * * * * *
上記等式中の
f(a) + grad f(a) ・h+ (1/2) Hf(a) [h]
を、「aにおけるfの2次の近似多項式」「aにおけるfの2次のテイラー多項式」と呼ぶ。
また、
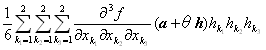
を、その剰余項と呼ぶ。
[→3階のテイラー定理冒頭]
|
|
|
|
|
|
|
|
定理:2変数関数の2次テイラー展開・2次多項式近似の剰余項の評価
|
|
|
[文献]
・高橋『微分と積分2』定理3.27(p.81):そのものずばり。
・黒田『微分積分学』8.6 (p.306):2次の項までのテイラー展開の表現。勾配ベクトル・ヘッセ行列の活用。
・神谷浦井『経済学のための数学入門』6.3.4定理6.3.5(p.234).
※活用例:極値問題―2階十分条件
※対照→n変数関数の2次テイラー展開
|
行列・ベクトル・Σを用いない表現
|
| 設定 |
2変数関数z=f(x,y)をC2級とする。 |
| 本題 |
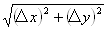 →0 →0
とすると、
f(x0+Δx, y0+Δy)= f(x0, y0)
+(Δx)fx(x0, y0)+(Δy) fy(x0, y0)
+(1/2){(Δx)2 fxx(x0, y0)+2(Δx)(Δy) fxy(x0, y0)+(Δy)2 fyy(x0, y0)}
+o( (Δx)2+(Δy)2 )
これを、ランダウのオーo( )の定義に遡って書き下すと、次のようになる。
f(x0+Δx, y0+Δy)= f(x0, y0)
+(Δx) fx(x0, y0)+(Δy) fy(x0, y0)
+(1/2){(Δx)2 fxx(x0, y0)+2(Δx)(Δy) fxy(x0, y0)+(Δy)2 fyy(x0, y0)}
+R3
とおくと、
(1)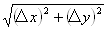 → 0 とすると、R3 → 0 → 0 とすると、R3 → 0
(2)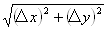 → 0 とすると、(Δx)2+(Δy)2→ 0 → 0 とすると、(Δx)2+(Δy)2→ 0
(3)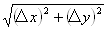 → 0 とすると、R3/{(Δx)2+(Δy)2}→ 0 → 0 とすると、R3/{(Δx)2+(Δy)2}→ 0
が満たされる。[(2)は自明だから、ここでは重要でない]
|
| ベクトル・行列表現 |
|
|
設定
|
x0,h :実2次元数ベクトル(縦ベクトル)
つまり、x0=t(x0,y0)
h=t(Δx,Δy)
f : 2変数実数値関数
つまり、f :R2⊃D→R
grad f (~) : ~におけるfの勾配ベクトル
Hf(~) :~におけるfのヘッセ行列 |
|
| 本題 |
f(x0+h)= f(x0) + grad f(x0) ・h+ (1/2) th Hf(x0)h +o(∥h∥2) (∥h∥→0)
これを、ランダウのオーo( )の定義に遡って書き下すと、次のようになる。
f(x0+h)= f(x0) + grad f(x0) ・h+ (1/2) th Hf(x0)h+R3
とおくと、
(1)∥h∥→0 とすると、R3 → 0
(2)∥h∥→0 とすると、∥h∥2→ 0
(3)∥h∥→0 とすると、R3/{∥h∥2}→ 0
が満たされる。[(2)は自明だから、ここでは重要でない]
|
| ベクトル・行列・2次形式を用いた表現 |
|
|
設定
|
x0,h:実2次元数ベクトル
つまり、x0=t(x0,y0)
h=t(Δx,Δy)
f :2変数実数値関数。つまり、「f :R2⊃D→R」
grad f (~) : ~におけるfの勾配ベクトル
Hf(~) :~におけるfのヘッセ行列
Hf(~) [h] :「~におけるfのヘッセ行列」によって定まる
h=t(Δx,Δy)についての二次形式 |
| 本題 |
f(x0+h)= f(x0) + grad f(x0) ・h+ (1/2) Hf(x0) [h] + o(∥h∥2) (∥h∥→0)
これを、ランダウのオーo( )の定義に遡って書き下すと、次のようになる。
f(x0+h)= f(x0) + grad f(x0) ・h+ (1/2) Hf(x0) [h] +R3
とおくと、
(1)∥h∥→0 とすると、R3 → 0
(2)∥h∥→0 とすると、∥h∥2→ 0
(3)∥h∥→0 とすると、R3/{∥h∥2}→ 0
が満たされる。[(2)は自明だから、ここでは重要でない] |
|
|
|
2変数関数のテイラーの定理
[和達『微分積分』125-7;吹田新保『理工系の微分積分学』168-9;小形『多変数の微分積分』70-3.;小平『解析入門2』§5.2-f(p.284);加藤『微分積分学原論』定理15.3(p.188)]
(舞台設定)
f(x,y)は領域DでCn級である2変数関数、
g1(t)= a+ht、g2(t)=b+kt (a,h,b,k :定数) は区間I={t|0≦t≦1}で定義された関数で、
t∈Iならば、つねに( g1(t) , g2(t) ) ∈Dであるとする。
(本題)
f(a+h, b+k)= f(a, b)
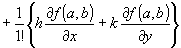
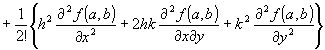
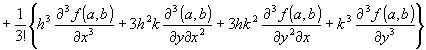
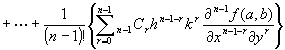
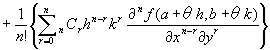 …①
…①
を満たすθ( 0<θ<1 )が存在する。
※対照せよ→1変数関数のテイラーの定理/n変数関数のテイラーの定理
※活用例→2変数関数の極値判定
※基礎知識:n!(階乗),∂(2変数関数の偏微分・高階偏微分),nCr(Combination)
(略記法)
式①を以下のように略記することが一般的。
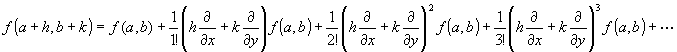
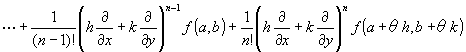
※ 二項定理より、
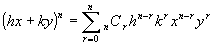
各項の係数が同じで
x,yの次数とx,yの微分の階数が同じところから。
※同じ略記法: 二つの1次関数と2変数関数との合成関数のn回微分
※類似の略記法:2変数関数の高階全微分
→[トピック一覧:2変数関数の平均値の定理・テイラーの定理]
→総目次
(証明:2変数関数のテイラーの定理)
Step0:
f(x,y)は領域DでCn級である2変数関数、
g1(t)= a+ ht、g2(t)= b+ kt (a,h,b,k :定数) は区間I={t|0≦t≦1}で定義された関数で、
t∈Iならばつねに( g1(t) , g2(t) ) ∈Dであるとする。
f(x,y)、g1(t)= a+ ht、g2(t)= b+ ktの合成関数 f(g1(t), g2(t)) = f(a+ ht, b+ kt) を、
tの一変数関数とみて、F(t) とおく。
すなわち、
F(t)=f(g1(t), g2(t)) = f(a+ ht, b+ kt)…①
このとき、F(t) は区間I={t|0≦t≦1}でCn級である。
(∵n回連続微分可能な関数の合成関数のn回連続微分可能性)
Step1:
F(t)は1変数関数だから、1変数関数のテイラーの定理によって、p,qが区間I={t|0≦t≦1}に含まれるならば、
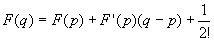
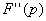
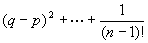
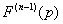
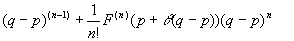
を満たすθが(0,1)内に存在する。
p=0, q =1としても区間I={t|0≦t≦1}に含まれるので、これは成り立ち、
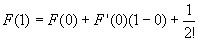
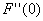
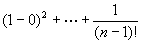
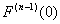
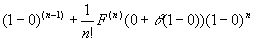
を満たすθが(0,1)内に存在する。
すなわち、
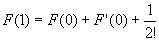
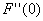
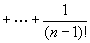
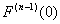
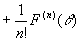 …②
…②
を満たすθが(0,1)内に存在する。
Step2: ②式のうち、F(1)、F(0)の計算。
①より、F(1)= f(a+ h・1, b+k・1) = f(a+h, b+k) …③
①より、F(0)= f(a+ h・0, b+k・0) = f(a, b) …④
Step3: ②式のうち、F(n)(0)の計算。
合成関数F(t)= f(a+ ht, b+ kt)のn階導関数の公式より、
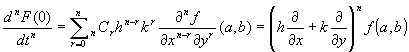 …⑤
…⑤
Step4: ②式のうち、F(n)(θ)の計算。
合成関数F(t)= f(a+ ht, b+ kt)のn階導関数の公式より、
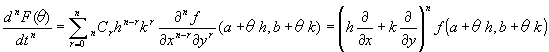 …⑥
…⑥
Step5:③④⑤⑥を②へ代入すれば、②は以下のように言いかえられる。
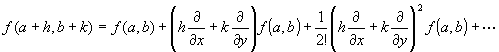
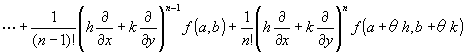
(証明終わり)
→[トピック一覧:2変数関数の平均値の定理・テイラーの定理]
→総目次
2変数関数のテイラー級数
→小平『解析入門II』p.293.
2変数関数のテイラー展開
→小平『解析入門II』p.293.
→[トピック一覧:2変数関数の平均値の定理・テイラーの定理]
→総目次
(reference)
小平邦彦『解析入門II』 (軽装版)岩波書店、2003年 p.284-294;。
和達三樹『理工系の数学入門コース1・微分積分』岩波書店、1988年、pp.125-127.
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.168-169.
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.160-161。
高橋陽一郎『岩波講座現代数学への入門:微分と積分2』 岩波書店、1995年、pp.97-98。
小形正男『理工系数学のキーポイント7:多変数の微分積分』岩波書店、1996、pp. 66-73.
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、pp.232-235.
高木貞治『解析概論 改訂第三版』岩波書店、1983年、pp.64-67.
杉浦光夫『解析入門』岩波書店、1980年、pp.99-102:1変数実数値関数に関するテイラーの定理;146-9多変数実数値関数に関するテイラーの定理. ただし、いきなり多次元。
→[トピック一覧:2変数関数の平均値の定理・テイラーの定理]
→総目次
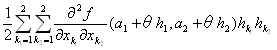
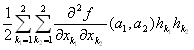
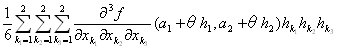
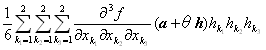
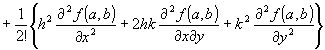
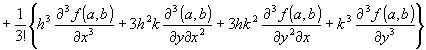
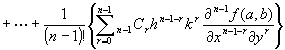
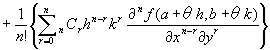 …①
…①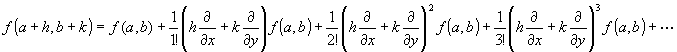
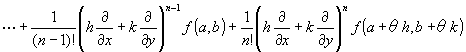
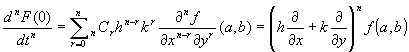 …⑤
…⑤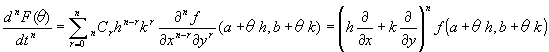 …⑥
…⑥