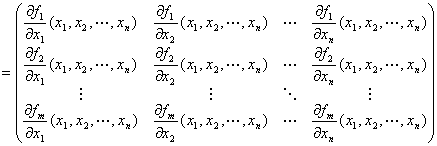n変数関数のグラディエント・ヤコビアン・ヘッシアン・ラプラシアン

　・定義：n変数関数の勾配ベクトル/ヤコビ行列・ヤコビアン・ヤコビ行列式・関数行列式
　・定義：ヘッセ行列・ヘッシアン・ヘッセ行列式/ラプラスの演算子・ラプラシアン

【関連ページ】

　・n変数関数について　　　　　　　　　　　　：　偏微分/高次の偏微分/全微分/高階全微分/合成関数の微分/平均値定理･テイラーの定理/極値問題/陰関数定理/逆関数定理/ラグランジュ未定乗数法
　・グラディエント・ヤコビアン・ヘッシアンについて　：　2変数関数の勾配ベクトル・ヤコビアン・ヘッシアン/ベクトル値関数の勾配ベクトル・ヤコビアン・ヘッシアン
　→総目次



定義　：　n変数関数の勾配ベクトル　gradient vector　


定義


n変数関数y=f (x1,x2,…,xn )の勾配ベクトル・グラディエントgradientとは、
　　y=f (x1,x2,…,xn )のx1に関する偏導関数,
　　y=f (x1,x2,…,xn )のx2に関する偏導関数,
　　　　　　　　　　　　　　　：
　　　　　　　　　　　　　　　：
　　y=f (x1,x2,…,xn )のxnに関する偏導関数
を並べたベクトルのこと。
すなわち、
　

 [文献]
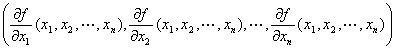
・岡田『経済学・経営学のための数学』3.3(p.124)
・西村『経済数学早わかり』3章-3.3 (p.125);
・神谷浦井『経済学のための数学入門』6.3.2 (p. 227) ;補題7.3.1-2(pp.281-4):凸性の判定
・黒田『微分積分学』8.3.3 (p.288);
・松坂『解析入門4』18.2H定理5(p.113):関数の凸性の判定。
cf.2変数関数の勾配ベクトル
　

　

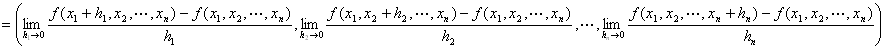
記法

・ n変数関数y=f (x1,x2,…,xn )の勾配ベクトル・グラディエントを、
　　∇f　　grad f　　
　などとあらわす。
　なお、記号∇は「ナブラ」と呼ばれる。
・点(a1,a2,…,an)におけるfの勾配ベクトル・グラディエントの値を、
　　∇f(a1,a2,…,an)　　grad f (a1,a2,…,an)　　
　などとあらわす。
　　　

 　
※ 解釈：fの最大傾斜方向を表し、その長さは傾きの最大値を与える
※ 活用例：臨界点・臨界値、極値、関数の凸性の判定、ラグランジュの未定乗数法

→トピック一覧：微分演算子　
→総目次

定義：n変数関数のヤコビ行列　Jacobian Matrix　・　ヤコビアン（ヤコビ行列式Jacobian Determinants・関数行列式functional determinant）


定義


m個の n変数関数 f 1 (x1,x2,…,xn ), f 2 (x1,x2,…, xn ),…, f m (x1,x2,…,xn )の勾配ベクトル
　　　　grad f 1 =∇f 1 , grad f 2 =∇f 2 ,…, grad f m =∇fm　
を、
縦に並べた以下のm行n列の行列をヤコビ行列と呼ぶ。　　
　
　

 [文献]
神谷浦井『経済学のための数学入門』6.3.2 (p. 227) ;
西村『経済数学早わかり』3章-5.0 (p.149);
黒田『微分積分学』8.3.5 (p.292);
小平『解析入門II』363;
Rudin『現代解析学』9.27(p.225)
Chiang,Fundamental Methods of Mathematical Economics 7.6 (p.184)

定義

 ヤコビ行列の行列式　　
　　　
　を、関数行列式ないしはヤコビアンと呼び、簡略化して表す場合には、
　記号J(x,y)、
　　　
　などを用いる。

※

 活用例：　積分の変数変換、逆関数の定理


→トピック一覧：微分演算子　
→総目次


定義：n変数関数のヘッセ行列・ヘッシアンHessian（ヘッ セ行列式）


定義


・「 n変数関数y=f (x1,x2,…,xn )のヘッセ行列」とは、
　　 n変数関数y=f (x1,x2,…,xn )のすべての第二次偏導関数を、
　　以下のようにn 行n列に並べた行列のこと。
　　　　
　　このヘッセ行列の(i,j)成分には、
　　 f (x1,x2,…,xn )のxi に関する偏導関数を、xjで偏微分して出てきた2階偏導関数
　　が置かれている。
・「(a1, a2,…,an)における n変数関数y=f (x1,x2,…,xn )のヘッセ行列」とは、
　　 n変数関数y=f (x1,x2,…,xn )のすべての第二次偏導関数が(a1, a2,…,an)でとる値を、
　　以下のようにn 行n列に並べた行列のこと。
　　　　　
　
[文献]
・松坂『解析入門4』 18.2-Gヘッセ行列(p.110);H定理6(p.115):関数の凸性の判定。
・神谷浦井『経済学のための数 学入門』6.3.2(pp.227-8)定理7.3.8(p.284):凸性の判定
・黒田『微分積分 学』8.6 (p.306):2次の項までのテイラー展開の表現。
・西村『経済数学早わ かり』3章§4 (p.138)
・布川ほか『線形代数と凸 解析』8.4凸関数の一般化(p.198)。

cf.2変 数関数のヘッセ行列・ヘッシアン
　

・ヘッセ行列の行列式を、ヘッシアンと呼ぶ。

 　

記法

・「(a1, a2,…,an)における n変数関数y=f (x1,x2,…,xn )のヘッセ行列」は、
　　Hf(a1, a2,…,an)　　H (a1, a2,…,an)　
　などと表す。　

　
　 　

※

 活用例：n変 数関数のテイラー展開の二次の項の表現/極 大の2階十分条件/極 小の2階十分条件/関数の凸性の判定、　

定義：n変数関数のラプラスの演算子（ラプラシアンLaplacian）　　記法：Δf　　

【定義】
　
　n変数関数f ( x1 , x2 , …,  xn )の各変数に関する第二次偏導関数の和
　　　　
【文献】

　黒田『微分積分学』8.4.1 (p.298);

→トピック一覧：微分演算子　
→総目次

定義：n変数関数の発散　divergence　　記法：divA

→ガウスの定理
[文献]
小形『多変数の微分積分』165-170:div;


定義：ローテーション　rotation　　記法:rotA

→ストークスの定理



（reference）

布川昊,谷野哲三,中山弘隆『線形代数と凸解析』コロナ社、1991年、8.4凸関数の一般化(p.198)。
西村和雄『経済数学早わかり』日本評論社、1982年、3章§4極値問題-定符号行列(p.138)。
黒田成俊『21世紀の数学1:微分積分学』共立出版株式会社、2002年、8.6多変数関数の極大極小(p.306)。

小形正男『理工系数学のキーポイント7:多変数の微分積分』岩波書店、1996、pp. 53-55:gradient;86-110:Jacobian;78:Hessian;.33:Laplacian.165-170:div;177-181:rot 1.
笠原皓司『微分積分学』サイエンス社、1974年、5.3節(pp.164-5)7.3節 (pp.266-270)。
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、p.227-
.
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.174-5:grad.;204:ヤコビアン;.227-30:∇・ラプラシアン
高橋一『経済学とファイナンスのための数学』新世社、1999年、p.148。
高橋陽一郎『岩波講座現代数学への入門：微分と積分2』 岩波書店、1995年、pp.85-86。ヘッセ行列と極値。
小平邦彦『解析入門II』 (軽装版)岩波書店、2003年、p.363.。ヤコビ行列のみ。
和達三樹『理工系の数学入門コース1・微分積分』岩波書店、1988年、pp.135ラプラシアン;pp.ヤコビアン152-53.
杉浦光夫『解析入門』岩波書店、1980年、pp.124-126 grad;. 132-135.ヤコビアン　ただし、いきなり多次元。
高木貞治『解析概論　改訂第三版』岩波書店、1983年、p. 316:gradF;297:関数行列式.
竹之内脩『経済・経営系数学概説』新世社、1998年、pp.110-113:2変数関数のヘッシアンと極値。
住友洸（たけし）『大学一年生の微積分学』現代数学社、1987年,pp.83-84:Laplacian;92:Jacobian;
日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年。