�����I��
��`
�y�����I�Ȓ�`�z
�uy=f (x)�͓_x0�Ŕ����\�v�Ƃ́A
�@y=f (x)���_( x0, f (x0) )�Őڂ���uy=f (x)�̐ڐ��v
�@�@�@�@y = f (x0)+A(x�|x0)
�@��
�@�����ЂƂ����邱�Ƃ������A
�@���̐ڐ��̌X��A���A�u�_x0�ɂ����� f (x) �������W���v�ƌĂԁB�@
��y = f (x0)+A(x�|x0)�ŕ\����Ȃ��ڐ��i�Ⴆ��y���ɕ��s�Ȑڐ��j���@�@�@�@�@
�@�����邱�Ƃ����邪�A
�@�����ł́A���̂悤�Ȑڐ���ڐ����珜�O���āA
�@y = f (x0)+A(x�|x0)�ŕ\�����ڐ��݂̂�ڐ��ƌĂсA
�@y = f (x0)+A(x�|x0)�ŕ\�����ڐ�����{���������邱�Ƃ��A
�@�����\�ƌĂԁB
�@�@[�����Y�w��͓����x��12 (p.86)]
(��)
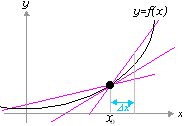
���}��y=f (x)�͓_x0�Ŕ����\�B�@�@
�@�@�@

�@�@�@�_x0��y=f (x)�ɐڂ���
�@�@�@�uy=f (x)�̐ڐ��v��
�@�@�@��{���������Ȃ��@
(��)
���}��y=f (x)�͓_x0�Ŕ����\�B
�@�@�@

�@�@�@�_x0��y=f (x)�ɐڂ���
�@�@�@�uy=f (x)�̐ڐ��v��
�@�@�@��{���������Ȃ��@�@�@�@
�@
(��)�@
���}��y=f (x)=�bx�b�͓_x=�O�Ŕ����\�łȂ��B�@
�@�@

�@�@�_x=�O��y=f (x)=�bx�b�ɐڂ���
�@�@�uy=f (x)�̐ڐ��v�́A
�@�@���낢�������B
�@
(��)�@
���}��y=f (x)=x1/3�͓_x=�O�Ŕ����\�łȂ��B�@
�@�@�@

�@y�����A�_x=�O��y=f (x)=x1/3�ɐڂ��邪�A
�@y����y=f (x0)+A(x�|x0)�̂������ŕ\����Ȃ�
�@�̂ŁA�ڐ��Ƃ��ăJ�E���g���Ȃ��B�@�@
���쉻
�Ƃ��낪�A
��L��
�@�@�uy=f (x)�́Ax=x0�������\�ŁAx=x0�ɂ����������W����A�ł���v
�Ƃ������Ƃ̍����I��`
�@�@�@�` y=f (x)�ɓ_x0�Őڂ���uy=f (x)�̐ڐ��v���A�����ЂƂ����A
�@�@�@�@�@�@�@���̐ڐ��̌X����A�ł���Ƃ������Ɓ@�`
�́A
��ʂ��̂�肩���Ő������\�ł���A
��������A
2�^�C�v�́u�����\�E�����W���̐��������ꂽ��`�v�������邱�ƂɂȂ�B�@�@�@
�������̃^�C�v�́A���Z�ŏK����`�ł���A
x0���烢x����x����������y=f (x)�̕��ϕω���
�@�@�@�@��y/��x = { f (x0+��x)�|f (x0)}/��x
�̓����ɒ��ڂ���B
���̃^�C�v�̒�`�́A
���ϐ����ɂ��Ē�`�����Δ����̃x�[�X�ƂȂ�B
�������̃^�C�v�́A
x0���烢x����x����������
�uy=f (x)�v�Ɓux0��ʂ钼��y=h (x) �v�Ƃ̊Ԃ̌덷
�@�@�@f (x+��x )�|h (x+��x )�@
�̓����ɒ��ڂ���B
���̃^�C�v�̒�`�́A
���ϐ����ɂ��Ē�`�����S�����̃x�[�X�ƂȂ�B
�������A���Â�̃^�C�v�́u�����\�E�����W���̐��������ꂽ��`�v���A�@�@
���l�ƂȂ邱�Ƃ́A�����܂ł��Ȃ��B


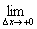
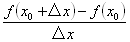 �@�@
�@�@




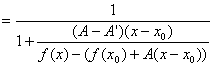 �@�@
�@�@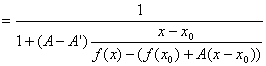 �@�@
�@�@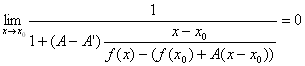 �@�@�@�@(Q''-1)
�@�@�@�@(Q''-1)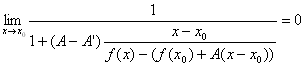 �@(Q''-1)�@
�@(Q''-1)�@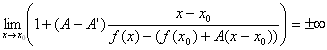 �@�@(Q''-2)�@
�@�@(Q''-2)�@
