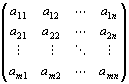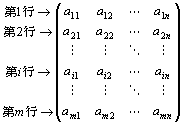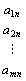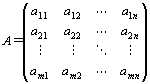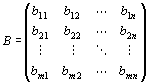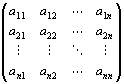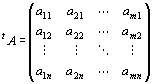実行列の定義

・定義：実行列[行･列･成分･型･記号]/同じ型の行列･行列の型の一致/等号
・定義：正方行列/矩形行列/零行列/行列単位/転置行列/対称行列/交代行列　

※実行列関連ページ：正方行列に関する様々な定義/行列の和･スカラー倍の定義/行列の積の定義/行列の積の性質/逆行列･正則行列･特異行列の定義/転置行列の性質/行列の代数系
　　　　　　　　　　実行列の標準形と階数/行列式/実行列の固有値　
※上位概念：体上の行列　
※線形代数目次・総目次・文献一覧
定義：実行列

設定


実行列は、以下の舞台設定上で、定義される。
R：実数をすべて集めた集合（実数体）　
aij：実数　　（実数体の元）　　


[文献]
・藤原『線形代数』2.1行列の定義と演算(p.28);
・斎藤『線形代数入門』2章§1-1〇(p.31);
・佐武『線形代数学』I-§2行列の演算(pp.4-7);
・砂田『行列と行列式』§2.2a(pp.54-56);
・グリーン『計量経済分析』2.2行列の用語(p.10);
・高橋『経済学とファイナンスのための数学』(p.14);

・松坂『解析入門4』15.1-A (pp.1-2);
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.1.1(p.48)
定義

・実行列とは、体として実数体Rを指定した「体上の行列」のことをいう。
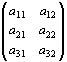
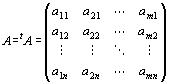
・具体的にいうと、実行列とは、実数aij を、
　次のように縦・横に並べて、長方形に配列したもの。
　　　　　

・行rowとは、行列の横の並びを指す。
　　　　
　行列の各行は、n次元横ベクトルと見なすことができるので、
　　　行列Aの第1行を「行列Aの第1行ベクトル」
　　　行列Aの第2行を「行列Aの第2行ベクトル」
　　　　　　　　：　　　　　　　　 ：　
　　　行列Aの第m行を「行列Aの第m行ベクトル」
　と呼ぶこともある。[斎藤『線形代数入門』2章§1-4〇(pp.35-36)]

※実行列は実ベクトル空間から実ベクトル空間への線形写像を表す（→定理/定理）。
　だから、実行列の分類・操作などが論じられる際には、
　　　　　それに対応する線形写像の分類・操作に思いをめぐらせるのが、肝要。

・列columnとは、行列の縦の並びを指す。
　行列　
　
　においては、
　第1列とは、
　　　　　
　第2列とは、
　　　　　
　第n列とは、
　　　　　
　のこと。　
　行列の各列は、n次元縦ベクトルと見なすことができるので、
　　　行列Aの第1列を「行列Aの第1列ベクトル」
　　　行列Aの第2列を「行列Aの第2列ベクトル」
　　　　　　　　：　　　　　　　　 ：　
　　　行列Aの第n列を「行列Aの第n列ベクトル」
　と呼ぶこともある。[斎藤『線形代数入門』2章§1-4〇(pp.35-36)]


・実行列の(i,j)成分element,entry,componentとは、
　実行列の第i行第j列におかれた実数aij のことを指す。
・実行列　
　
　においては、
　　　(1,1)成分とは、行列の第1行第1列におかれた実数a11 のこと、　　　
　　　(1,2)成分とは、行列の第1行第2列におかれた実数a12 のこと、
　　　　：　
　　　(m,n)成分とは、行列の第m行第n列におかれた実数amn のこと、
　　となる。　　

・m×n行列m×n matrix・m行n列行列・(m,n)行列・(m,n)型行列matrix of (m,n)-typeとは、
　mn個の実数を、m行n列に並べた行列のことをいう。　　


　たとえば、
　　　
　は、2×2行列ないし(2,2)型行列、
　　　　　
　は、3×2行列ないし(3,2)型行列。
　また、
　n次元横ベクトルは、1×n行列ないし(1,n)型行列。
　n次元縦ベクトルは、n×1行列ないし(n,1)型行列。

記号

・行列を書くたびに、成分をすべて書き出すのは、余りにわずらわしいので、
　　はじめに、　
　　　
　　などと定義したうえで、あとは、この英大文字で表すのが普通。


　(例)
　・単位行列I=(δi j)　　
　・ m×n行列A=(aij), B=(bij)にたいして、A＋B=(aij＋bij)　
　・k∈R, A=(aij)にたいして、kA=(kaij)　　　

・実行列Aの(i,j)成分を、Aijと表す。　　
・実行列Aの(i,j)成分をaijと一般的に表せることを、A=(aij)と略記する。


→[トピック一覧：実行列の定義]
→線形代数目次・総目次


定義：同じ型の行列、行列の型の一致

定義
「行列Aの型と行列Bの型が一致する」
「行列Aと行列Bは同じ型の行列である」とは、
　行列Aも行列Bも、両方とも、(m,n)型行列であること、
　すなわち、　
　　行列Aの行数と、行列Bの行数とが、一致し、
　　なおかつ、
　　行列Aの列数と、行列Bの列数とが、一致すること
　をいう。 		[文献]
・『岩波数学辞典』83行列(p.220);
・『高等学校代数幾何』(p.77)




→[トピック一覧：実行列の定義]
→線形代数目次・総目次

 　



定義：行列のあいだの等号

定義
・行列Aと行列Bについて、
　　「AとBが等しい」「A=B」とは、
　　AとBの型が一致し、かつ、Aの成分とBの成分がすべて一致することをいう。　
・つまり、A=Bとは、
　Aの行数もBの行数もともにm、Aの列数もBの列数もともにnで一致して、
　　　　　
　　　　　
　と、表せて、
　なおかつ　　
　　　i=1,2,…,m、　j=1,2,…,nに対して、aij=bij　
　であることを指す。
[文献]
・『岩波数学辞典』83行列(pp.219-220);
・斎藤『線形代数入門』2章§1(p.31);
・藤原『線形代数』2.1(p.22);
・グリーン『計量経済分析』2.3.1(p.12)



→[トピック一覧：実行列の定義]
→線形代数目次・総目次

 　


定義： n次正方行列square matrix

設定
n次正方行列square matrixは、以下の舞台設定上で定義される。
R：実数をすべて集めた集合（実数体）　
aij：実数　　（実数体の元）　
[文献]
・『岩波数学辞典』83行列(p.220);
・永 田『理系のための線形代数の基礎』1.4(p.23);
・グ リーン『計量経済分析』2.2(p.11) ;
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.1.1(p.49)
・斎藤『線形代数入門』2章§2(p.40);
・藤 原『線形代数』2.1(p.21);
・砂 田『行列と行列式』§2.2a(pp.54-56);
・高橋『経済学とファイナンスのための 数学』(p.14);
・松坂『解析 入門4』15.1-A (p. 3);

定義
(簡潔な定義)
　　n次正方行列square matrixとは、(n,n)型行列のこと。　　
(具体的な定義)
　　実数体R上のn次正方行列とは、
　　n2個の実数aij を、次のように、n行n列に並べた実行列のことをいう。
　　　　
　たとえば、
　　　
　は、2次正方行列である。

※正方行列についての諸概念： 対角成分、 対角和･トレース、 行列式、固有値・固有ベクトル、 対角化可能　　　　
※様々な正方行列：対角行列、 対称行列、 スカラー行列、 単位行列
※活用： Rn上 の一次変換は、 n次正方行列を用いて表現される。 [→ 標準基底に関する一次変換の表現行列 ]

→[トピック一覧：実行列の定義]
→線形代数目次・総目次


定義：矩形行列rectangular matrix

定義
正方行列 にたいして、正方行列 でない行列を、
　　矩形行列rectangular matrixと呼ぶこともある。
[文献]
・『岩波数学辞典』83行列(p.220);




→[トピック一覧：実行列の定義]
→線形代数目次・総目次

 　


定義：零行列　zero matrix
定義
 ・実数体R上の 零行列 とは、 実数 「０」 をのみを並べた 行列 のことをいう。　
・実数体R上の (m,n) 型零行列とは、 実数「０」 をm行n列 に並べた行列のことをいう。
・(m,n)型零行列を、 Om,nあるいは単にOなどと表す。
[文献]
・『岩波数学辞典』83行列(p.220);
・永田『理系のための線形代数の基礎』1.4(p.24);
・松坂『解析入門4』15.1-B (p. 3) ;
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.1.1(p.49)
・斎藤『線形代数入門』2章§1(p.32);
・藤原『線形代数』2.1(p.23);
・グリーン『計量経済分析』2.3.3(p.13)
※ 零行列との和の演算則、零行列との積の演算則　

→[トピック一覧：実行列の定義]
→線形代数目次・総目次


定義：行列単位
定義
 ・行列単位Eijとは、
　　　( i, j )成分が実数1 、　　
　　　( i, j )成分以外の成分は、 すべて「実数０」
　となる 行列のことをいう。 		[文献]
・永田『理系のための線形代数 の基礎』1.4(p.24);




→[トピック一覧：実行列の定義]
→線形代数目次・総目次

 　


定義：転置行列transposed matrix

定義
(定義)
(m,n)型行列Aの転置行列transposed matrixとは、
　Aの行を列とし、 Aの列を行とした (n,m)型行列。　
　Aの(i,j)成分を (j,i)成分と してもつ (n,m)型行列 と言ってもよい。
(記号)　　　　
Aの転置行列を、tA 、A'などと表す。　
(具体的には)
　　　
ならば、　
　　　
[文献]
・『岩波数学辞典』83行列B(p.220);
・永 田『理系のための線形代数の基礎』1.8(p.42);
・斎藤『線形代数入門』2章§1(p.37);
・藤 原『線形代数』2.1(p.28);
・グ リーン『計量経済分析』2.3.2(p.12) ;
・戸田山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.1.1(p.49)
・高橋『経済学とファイナンスのための 数学』(p.14);
※ 転置行列の性質

→[トピック一覧：実行列の定義]
→線形代数目次・総目次

　
定義：実対称行列symmetric matrix


設定


実対称行列は、以下の舞台設定上で、定義される。
R：実数をすべて集めた集合（実数体）　
aij：実数　　（実数体の元）　　


[文献]
・『岩波数学辞典』83行列B(p.220);
・永田『理系のための線形代数の基礎』1.8(p.43);
・藤原『線形代数』2.1(p.28);
・高橋『経済学とファイナンスのための数学』(p.14);
・グリーン『計量経済分析』2.2(p.11)

　

※実行列は
　　　RnからRmへの線型写像　
　　　実ベクトル空間から実ベクトル空間への線形写像
　を表す（→定理/定理）。
　だから、実行列のタイプが論じられる際には、
　　　　　それに対応する線形写像のタイプに思いをめぐらせるのが、肝要。
　この「対称行列」というタイプの実行列は、
　　　　　Rn上の対称変換
　　　　　実ベクトル空間上の対称変換
　というタイプの一次変換を表す。　

定義

対称行列とは、自らの転置行列と等しい行列のことをいう。
つまり、

が対称行列であるとは、　
　　　
ということであるが、
これは、
Aの行数と列数が一致し(m=n、ゆえにAは正方行列)であり、
かつ、
Aの成分が対角線に対して対称であること(aij=aji)を意味する。

→[トピック一覧：実行列の定義]
→線形代数目次・総目次

　

定義：交代行列alternating matrix,歪対称行列skew-symmetric matrix, 反対称行列antisymmetric matrix　　　
　[『岩波数学辞典』83行列B(p.220);永田『理系のための線形代数の基礎』1.8(p.43);
　　斎藤『線形代数入門』2章§1(p.37);藤原『線形代数』2.1(p.28)]



　　


→[トピック一覧：実行列の定義]
→線形代数目次・総目次

 　

(reference)
日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年、項目83行列(pp.219-)
線形代数のテキスト
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.4行列と一次写像(pp.23-6)。
佐武一郎『線形代数学(第44版)』裳華房、1987年、I.ベクトルと行列の演算§2行列の演算(pp.4-7)。
砂田利一『現代数学への入門：行列と行列式』2003年、§2.2一般の行列(pp.54-60).
藤原毅夫『理工系の基礎数学2：線形代数』岩波書店、1996年、2.1行列の定義と演算(pp.21-29)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第2章行列§1行列の定義と演算(pp.31-40)。

ホフマン・クンツェ『線形代数学I』培風館、1976年、一次方程式(pp.1-27)。
志賀浩二『数学30講シリーズ：線形代数30講』朝倉書店、1988年、17講線形写像と行列(pp.107-112)。


数理経済学のテキスト
西村和雄『経済数学早わかり』日本評論社、1982年、２章線形代数§2行列と行列式(pp.46-72)。
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、5章行列(pp.161-199):一次写像の行列表現を中心にしている。
高橋一『経済学とファイナンスのための数学』新世社、1999年、1.2ベクトルと行列(pp.6-25).
計量経済学のテキスト
William H. Greene（斯波・中妻・浅井訳） 『経済学体系シリーズ：グリーン計量経済分析I：改訂4版』エコノミスト社、2000年、第２章行列代数2.2行列の用語(pp.10-12);2.3行列の算法(pp.12-21)。
岩田暁一『経済分析のための統計的方法(第2版)』東洋経済新報社、1983年、12.1行列の演算(pp.269-277);12.4.2逆行列(pp.294-5)。


→[トピック一覧：実行列の定義]
→線形代数目次・総目次