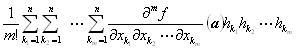|
|
|
定理:n変数関数の2次テイラー展開・2次多項式近似の剰余項の評価
|
| 要旨 |
(a1,a2,…,an)におけるfの2次近似多項式の剰余項は、
(a1,a2,…,an)までの距離の2乗より、高位の無限小。 |
[文献]
・黒田『微分積分学』8.6 (p.306):2次の項までのテイラー展開の表現。勾配ベクトル・ヘッセ行列の活用。
・神谷浦井『経済学のための数学入門』6.3.4定理6.3.5(p.234).
※活用例:極値問題―2階十分条件
※対照→2変数関数の2次テイラー展開
|
| 行列・ベクトル・Σを用いない表現 |
|
設定
|
n変数実数値関数y=f (x1,x2,…,xn)をC2級とする。 |
| 本題 |
f (a1+h1,a2+h2,…,an+hn)= f (a1,a2,…,an)
+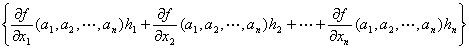
+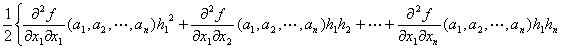
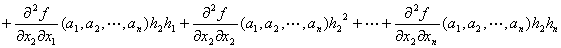
:
…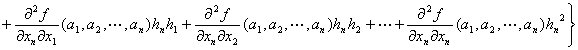
+o(‖(h1,h2,…,hn)‖2) (‖(h1,h2,…,hn)‖→0)
これを、ランダウのoの定義に遡って書き下すと、次のようになる。
f (a1+h1,a2+h2,…,an+hn)= f (a1,a2,…,an)
+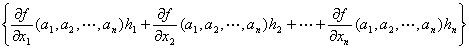
+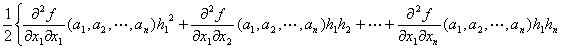
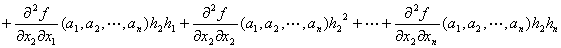
…
:
…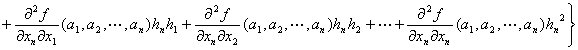
+R3
とおくと、
(1) R3 → 0 ( ‖(h1,h2,…,hn)‖→ 0 )
かつ
(2) ‖(h1,h2,…,hn)‖2 → 0 ( ‖(h1,h2,…,hn)‖→ 0 )
かつ
(3) R3 / ‖(h1,h2,…,hn)‖2 → 0 ( ‖(h1,h2,…,hn)‖→ 0 )
が満たされる。[(2)は自明だから、ここでは重要でない]
|
| 勾配ベクトル・ヘッセ行列・2次形式を用いた表現 |
|
|
設定
|
f (x1,x2,…,xn):n変数実数値関数。C2級。
grad f (〜) : 〜におけるfの勾配ベクトル
Hf(〜) :〜におけるfのヘッセ行列
Hf(〜) [h1,h2,…,hn] :「〜におけるfのヘッセ行列」によって定まる(h1, h2, h3, …, hn)についての二次形式 |
| 本題 |
f (a1+h1,a2+h2,…,an+hn)= f (a1,a2,…,an)
+ gradf(a1,a2,…,an)・(h1, h2, h3, …, hn)
+(1/2)Hf(a1,a2,…,an)[h1,h2,…,hn]+o(‖(h1,h2,…,hn)‖2) (‖(h1,h2,…,hn)‖→0)
これを、ランダウのoの定義に遡って書き下すと、次のようになる。
f (a1+h1,a2+h2,…,an+hn)= f (a1,a2,…,an)+gradf(a1,a2,…,an)・(h1, h2, h3, …, hn)+(1/2)Hf(a1,a2,…,an)[h1,h2,…,hn]+R3
とおくと、
(1) R3 → 0 ( ‖(h1,h2,…,hn)‖→ 0 )
かつ
(2) ‖(h1,h2,…,hn)‖2 → 0 ( ‖(h1,h2,…,hn)‖→ 0 )
かつ
(3) R3 / ‖(h1,h2,…,hn)‖2 → 0 ( ‖(h1,h2,…,hn)‖→ 0 )
が満たされる
|
| Σの表現 |
|
|
設定
|
n変数実数値関数y=f (x1,x2,…,xn)をC2級とする。 |
|
| 本題 |
f (a1+h1,a2+h2,…,an+hn)= f (a1,a2,…,an)+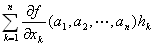 + +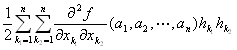 +o(‖(h1,h2,…,hn)‖2) (‖(h1,h2,…,hn)‖→0) +o(‖(h1,h2,…,hn)‖2) (‖(h1,h2,…,hn)‖→0)
これを、ランダウのoの定義に遡って書き下すと、次のようになる。
f (a1+h1,a2+h2,…,an+hn)= f (a1,a2,…,an)+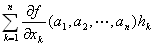 + +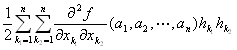 +R3 +R3
とおくと、
(1) R3 → 0 ( ‖(h1,h2,…,hn)‖→ 0 )
かつ
(2) ‖(h1,h2,…,hn)‖2 → 0 ( ‖(h1,h2,…,hn)‖→ 0 )
かつ
(3) R3 / ‖(h1,h2,…,hn)‖2 → 0 ( ‖(h1,h2,…,hn)‖→ 0 )
が満たされる。[(2)は自明だから、ここでは重要でない]
|
| ベクトル・行列表現 |
|
|
設定
|
x,a,h :実n次元数ベクトル(縦ベクトル)
つまり、x=t(x1, x2, x3, …, xn)
a=t(a1, a2, a3, …, an)
h=t(h1, h2, h3, …, hn)
f : n変数実数値関数。つまり、f :Rn⊃D→R
ただし、n変数実数値関数y=f (x)をC2級とする。
grad f (〜) : 〜におけるfの勾配ベクトル
Hf(〜) :〜におけるfのヘッセ行列
|
|
| 本題 |
f (a+h)= f(a)+gradf(a)h+(1/2)th Hf(a)h +o(‖h‖2) (‖h‖→0)
これを、ランダウのoの定義に遡って書き下すと、次のようになる。
f (a+h)= f(a)+gradf(a)h+(1/2)th Hf(a)h +R3
とおくと、
(1) R3 → 0 ( ‖h‖→ 0 )
かつ
(2) ‖h‖2 → 0 ( ‖h‖→ 0 )
かつ
(3) R3 / ‖h‖2 → 0 ( ‖h‖→ 0 )
が満たされる。[(2)は自明だから、ここでは重要でない]
|
| ベクトル・行列・2次形式を用いた表現 |
|
|
設定
|
x,a,h :実n次元数ベクトル
つまり、x=t(x1, x2, x3, …, xn)
a=t(a1, a2, a3, …, an)
h=t(h1, h2, h3, …, hn)
f : n変数実数値関数。つまり、f :Rn⊃D→R
ただし、n変数実数値関数y=f (x)をC2級とする。
grad f (〜) : 〜におけるfの勾配ベクトル
Hf(〜) :〜におけるfのヘッセ行列
Hf(〜) [h] :「〜におけるfのヘッセ行列」によって定まるh=t(h1, h2, h3, …, hn)についての二次形式 |
| 本題 |
f(a+h)= f(a)+grad f (a)h+(1/2)Hf(a)[h]+o(‖h‖2) (‖h‖→0)
これを、ランダウのoの定義に遡って書き下すと、次のようになる。
f (a+h)= f(a)+gradf(a)h+(1/2)Hf(a)[h] +R3
とおくと、
(1) R3 → 0 ( ‖h‖→ 0 )
かつ
(2) ‖h‖2 → 0 ( ‖h‖→ 0 )
かつ
(3) R3 / ‖h‖2 → 0 ( ‖h‖→ 0 )
が満たされる。[(2)は自明だから、ここでは重要でない]
|
|
|
|
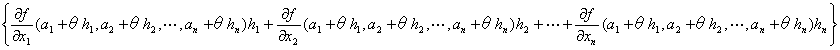
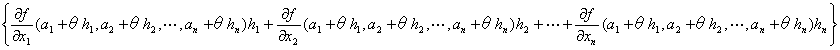
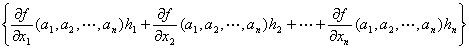
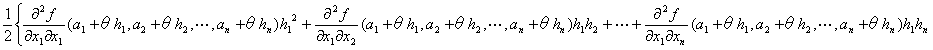
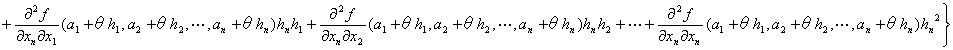
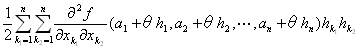
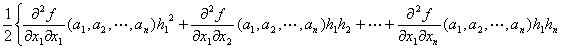
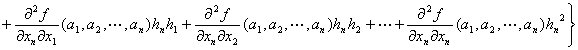
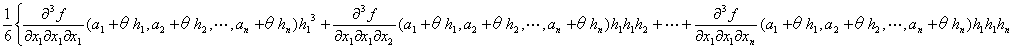
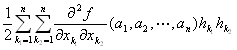
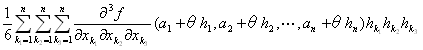
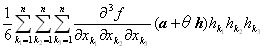
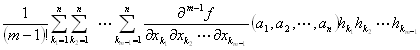
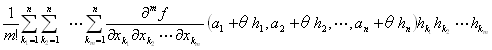
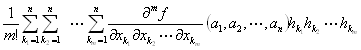
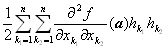 +…+
+…+