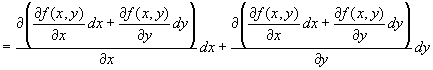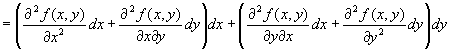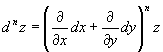2変数関数の高階全微分　

[トピック一覧：2変数関数の高階全微分]
　・2変数関数の2階の全微分
　・2変数関数の高階全微分
※全微分関連ページ：2変数関数の全微分　
※微分関連ページ： 1変数関数の微分(differential)、2変数関数の偏微分/高次の偏微分/微分演算子　
※2変数関数微分の応用：合成関数の微分、平均値定理･テイラーの定理、極値問題　　
　　　　　　　　　　　　　　陰関数定理、逆関数定理、ラグランジュ未定乗数法

→参考文献・総目次

定義：2変数関数の2階の全微分 the second-order total differential

　[高木『解析概論』59;. Chiang, Fundamental Methods of Mathematical Economics: Third Edition,.314.]
　　　　　※関連事項：二次形式　　
　　　　　※応用例：2変数関数の極値問題　
z = f ( x , y ) の1階の全微分　
　　　
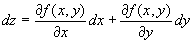
において、　　　
　　　
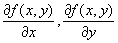
が微分可能ならば、　
2階の全微分として、　　　
　　　
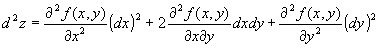
を得る。
　　　→2階偏微分の記法を確認せよ。　なお、　　
　　　　　　
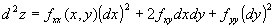
　　　　　と書いても同じ。　　　
（説明）　
　z=f (x,y)が領域Dの各点で全微分可能であるとき、
　点( x, y )∈Dにおけるz=f (x,y)の1階の全微分　
　　　　　
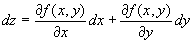
　の値は、点( x, y ) によって変わってくるから、領域D上の点( x, y )の関数。
　そこで、
　
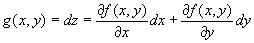
　とおく。　
　2階の全微分とは、1階の全微分であるg ( x, y ) を、もう一度全微分したもの。
　だから、全微分の定義をそのままg ( x, y )に適用して、　
　　　
　　　　　
　　　　　
　　　　　
　　　　　
　　　　　
　　　　　　　　∵　
　　　　　　　　　　
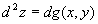
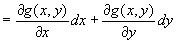
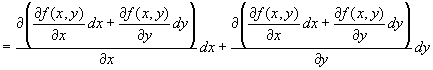
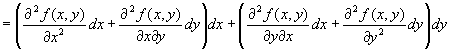
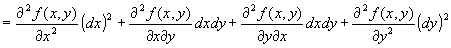
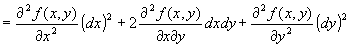
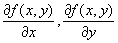
　　　　　　　　　が微分可能なので、youngの定理より、
　　　　　　　　　　

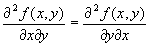
→[トピック一覧：2変数関数の高階全微分]
→総目次　

定義：2変数関数の高階の全微分 　[高木『解析概論』59. ]
　※必要な知識：高階偏微分、二項定理、組み合せ、全微分　
　z = f ( x , y ) の3階の全微分:
　
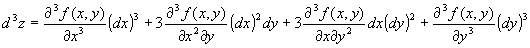
　z = f ( x , y ) のn階の全微分:
　
　　　
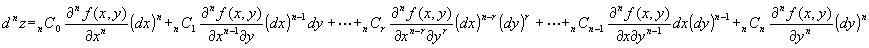
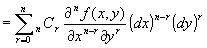
　つまり、z = f ( x , y ) をn階全微分は、(n+1)項からなる多項式となる。
　この (n+1)個の項を、第0項から第n項という風に数えあげて行った場合の第r項は、
　　　　二項係数×[ f ( x , y ) をxで(n-r)回偏微分、yでr回偏微分した導関数]×(dx)^n-r×(dy)^r　
　となっている。
　z = f ( x , y ) のn階の全微分の略記法：　
　n回全微分の式の各項から導関数を除いた
　　
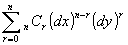
　は、二項定理より、(dx+dy) ⁿ に等しい。
　そこで、
　
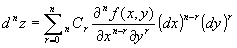
　は、
　
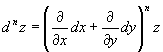
　と略記される。
　※類似例：二つの「1変数１次関数」と一つの「2変数関数」の合成関数の高階微分　

→[トピック一覧：2変数関数の高階全微分]
→総目次　

定義：3変数関数の2階の全微分　
　[高木『解析概論』59.; Chiang, Fundamental Methods of Mathematical Economics: Third Edition333. ]

→[トピック一覧：2変数関数の高階全微分]
→総目次　

（reference）

高木貞治『解析概論　改訂第三版』岩波書店、1983年、p. 59.
Chiang, Fundamental Methods of Mathematical Economics: Third Edition, McGraw Hill,1984,pp.308-319;333.

→[トピック一覧：2変数関数の高階全微分]
→総目次