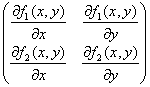・定義：2変数関数の勾配ベクトル/ヤコビ行列・ヤコビアン・ヤコビ行列式・関数行列式
　・定義：ヘッセ行列・ヘッシアン・ヘッセ行列式/ラプラスの演算子・ラプラシアン

　※関連ページ
　・グラディエント・ヤコビアン・ヘッシアン：n変数関数のケース/ベクトル値関数のケース
　・2変数関数の微分定義：偏微分/高階偏微分/方向微分/全微分/高階全微分　
　・2変数関数微分の応用：合成関数の微分/平均値定理･テイラーの定理/極値問題
　　　　　　　　　　　　　　陰関数定理/逆関数定理/ラグランジュ未定乗数法
　・2変数関数の概念：2変数関数の諸属性/極限/連続/極限の性質/矩形上の積分/点集合上の積分　
　→文献・総目次　

定義

2変数関数f ( x, y )の勾配ベクトルgrad f ( x, y ), ∇f ( x, y )とは、
　f (x,y )のx, yそれぞれに関する偏導関数を並べたベクトル。
すなわち、

[文献]
・小形『多変数の微分積分』pp. 53-55

・黒田『微分積分学』8.3.3 (p.288).
・Lang,Undergraduate Analysis,15-§2(p.322);
・de la Fuente, Mathematical Methods and Models for Economists, PartI-4-2 (pp.166) ：n変数関数.

※n変数関数の勾配ベクトル

f (x,y )が点(x₀,y₀)で(全)微分可能ならば、
f (x,y )の点(x₀,y₀)における微分係数は、
点(x₀,y₀)における勾配ベクトル
　　　grad f (x₀,y₀)＝（∂f (x₀,y₀)/∂x , ∂f (x₀,y₀)/∂y）
に等しくなる。
[→定理]

※

f (x,y )が点(x₀,y₀)で(全)微分可能ならば、
f (x,y )の点(x₀,y₀)における方向微分係数は、
　　点(x₀,y₀)における勾配ベクトルgrad f (x₀,y₀)＝（∂f (x₀,y₀)/∂x , ∂f (x₀,y₀)/∂y）
から計算可能。
[→公式]

※

活用例：極値、ラグランジュの未定乗数法

→[トピック一覧：微分演算子]
→総目次

定義

2変数関数f₁(x,y), f₂(x, y)の勾配ベクトルgrad f₁=∇f₁、grad f₂=∇f₂を、
　縦に並べた以下の行列をヤコビ行列と呼ぶ。　　
　　　　

[文献]
・小平『解析入門II』363;
・小形『多変数の微分積分』86-110;
・吹田新保『理工系の微分積分学』204;
・笠原『微分積分学』7.3節 (pp.266-270)
・杉浦『解析演習』�U章§2-2.3(p. 89) ：n変数実関数

定義

ヤコビ行列のの行列式　　
　　
　　　
　を、関数行列式ないしはヤコビアンと呼び、簡略化して表す場合には、
　記号J(x,y)、
　　　
　などを用いる。

※n変数関数のヤコビ行列

※

活用例：　積分の変数変換、逆関数の定理

→[トピック一覧：微分演算子]
→総目次

定義

・「2変数関数f ( x, y )のヘッセ行列」とは、
　2変数関数f ( x, y )のすべての第二次偏導関数を、
　次のように並べた2×2行列のこと。
　　　　　　

[文献]
小平『解析入門II』363;
小形『多変数の微分積分』86-110;
吹田新保『理工系の微分積分学』204;
笠原『微分積分学』7.3節 (pp.266-270)


※n変数関数のヘッセ行列

　　この行列式　　
　　
　を、ヘッシアンと呼ぶ。

※

活用例：極値　

→[トピック一覧：微分演算子]
→総目次

定義

　2変数関数f ( x, y )のx, yそれぞれに関する第二次偏導関数の和。
　　　　

→[トピック一覧：微分演算子]
→総目次

定義

[文献]
小形『多変数の微分積分』165-170:div;

→ガウスの定理

→[トピック一覧：微分演算子]
→総目次

定義

[文献]

→ストークスの定理

→[トピック一覧：微分演算子]
→総目次