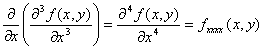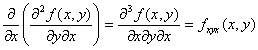2変数関数の高次の偏微分

・定義：2変数関数の2 階偏導関数・第2次偏導関数/第n次偏導 関数・n階偏導関数・高階偏導関数/Cⁿ級
・偏 微分の順序についての性質：
　　　・定理/Youngの定理/Schwarzの定理　
　　　・Cⁿ級 関数のn回までの偏微分は偏微分の順序を換えても変わらない

【関連ページ】
　 ・高次の微分：1変 数関数の高次の微分/2変 数関数の高次の全微分
　 ・2変 数関数の偏微分：偏微分可能・偏微分係数・偏導関数の定義/微分演算子
　 ・微分定義：1変 数関数の微分/2変 数関数の全微分/方向微分
　 ・2変 数関数微分の応用：合成関数の微分/平均値定理･テイラーの定理/極値問題
　　　　　　　　　　　　　　陰関数定理/逆関数定理/ラグランジュ未定乗数法

定義

2変数関数z=f (x,y)の偏導関数に、さらにその偏導関数が存在するならば、
それらを、2階偏導関数、第2次偏導関数などと呼ぶ。　
2変数関数z=f (x,y)の第2次(2階)偏導関数として、
以下の4種を考えることができる。
　　（→これらを一定のパターンに並べたのが、Hesse行列）
・type-I. まず、xで偏微分して、次もxで偏微分。　
　　　　　関数z=f (x,y)のxに関する偏導関数 f _x (x,y)　を、　
　　　　　さらにxで偏微分して出てきた導関数　
　　　　　　
　　　　　（記法）　
　　　　　　　f _{x x}(x,y)　　
　　　　　　　　　

[文献]
『微分積分』pp.118-119;
吹田新保『理工系の微分積分学』pp.162-163.

※類概念：
　　1変数関数の第2次(2階)偏導関数

・type-II. まず、xで偏微分して、次はyで偏微分。　
　　　　　関数z=f (x,y)のxに関する偏導関数 f _x (x,y)　を、　
　　　　　さらにyで偏微分して出てきた導関数　
　　　　　　
　　　　　　（記法）　
　　　　　　　　f _{x y}(x,y)　
　　　　　　　　　　
・type-III. まず、yで偏微分して、次もyで偏微分。　
　　　　　　関数z=f (x,y)のyに関する偏導関数 f _y (x,y)　を、　
　　　　　　さらにyで偏微分して出てきた導関数　
　　　　　　　
　　　　　　（記法）　
　　　　　　　　f _{y y}(x,y)　　
　　　　　　　　　　
・type-IV. まず、yで偏微分して、次はxで偏微分。　
　　　　　関数z=f (x,y)のyに関する偏導関数 f _y (x,y)　を、　
　　　　　さらにxで偏微分して出てきた導関数　
　　　　　　
　　　　　　（記法）　
　　　　　　　　　f _yx(x,y)　　
　　　　　　　　　　　

定義

2階以上の偏導関数を総称して高階偏導関数と呼ぶ。　
(z= f (x,y)の第n次(n階)偏導関数の表記例)　　
　　　　　　
　　　　　　

※類概念：
　　1変数関数の第n次(n階)偏導関数

定義

関数f (x,y)が
「D上でn回連続微分可能」
ないし
「 D上で C ⁿ級 function of class C-n 」であるとは、　
関数f (x,y)が領域D上でn階までのあらゆる偏導関数をもち、
それらがすべてD上 で連続であることをいう。

※類概念：1変 数関数のCⁿ級

※

全微分可能との関係、偏微分の順序との関係

定理

ある領域Dにおいて
関数f (x,y)の偏導関数 f _x (x,y) , f _y (x,y)、2階偏導関数 f _{x y} (x,y) , f _yx (x,y) が存在して、
f _{x y} (x,y) , f _yx (x,y)　が連続
ならば、　　
f _{x y} (x,y) ＝ f _yx (x,y) 　が成り立つ

[文献]
小平『解析入門II』pp.272-273.

Youngの定理　

領域Dにおいて
関数f (x,y)の偏導関数 f _x (x,y) , f _y (x,y) が存在して微分可能
ならば、　
f _{x y} (x,y) ＝ f _yx (x,y) 　が成り立つ。　

[文献]
小平『解析入門II』pp.273-274.
高木『解析概論』p.58.

Schwarzの定理

ある領域Dにおいて
関数f (x,y)の偏導関数f _x (x,y) , f _y (x,y) ,2階偏導関数 f _{x y} (x,y)が存在して、　
　　f _{x y} (x,y)が連続ならば　　
2階偏導関数f _{y x} (x,y)も存在して、
　　f _{x y} (x,y) ＝ f _yx (x,y) 　が成り立つ。

[文献]
吹田・新保『理工系の微分積分学』p.163.;
小平『解析入門II』pp.273-274.

偏微分の順序についての結論

　以上の諸定理より、　　
　C ⁿ級関数f (x,y)について、n回までの偏微分は微分の順序を換えても変わらない。