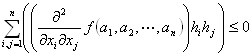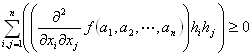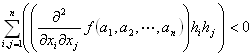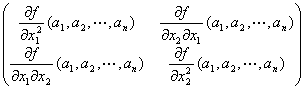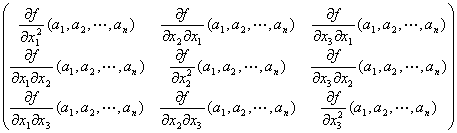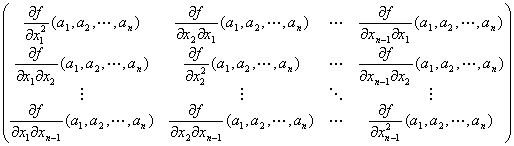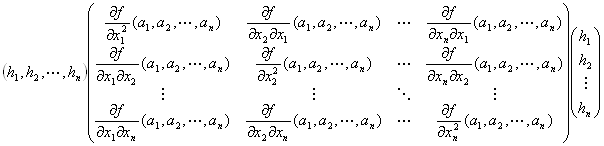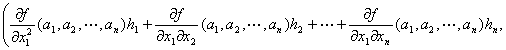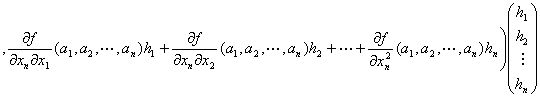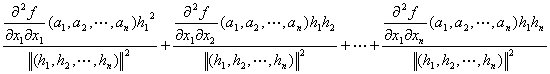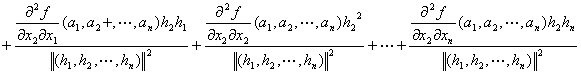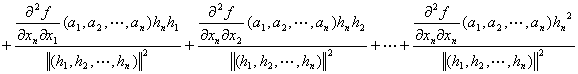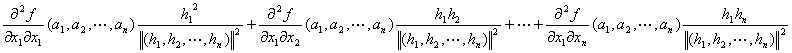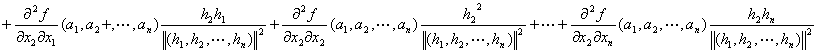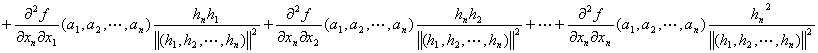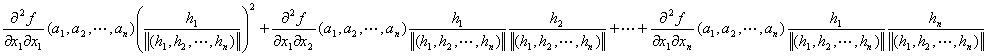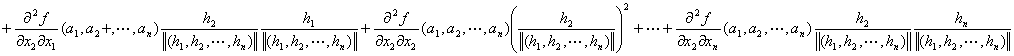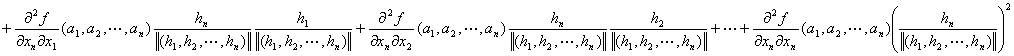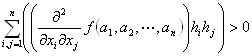|
ただし、
Q(h1,h2,…,hn)
=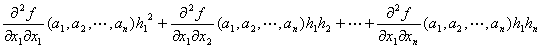
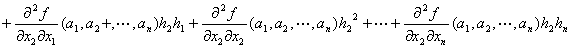
+…
:
…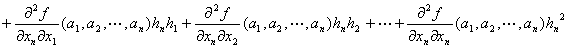
Ⅰ.
テイラー展開の公式によって、
f (a1+h1,a2+h2,…,an+hn)= f (a1,a2,…,an)+gradf(a1,a2,…,an)・(h1,h2,…,hn)+(1/2)Q(h1,h2,…,hn)+R3
とおくと、
R3 → 0 ( ∥(h1,h2,…,hn)∥→ 0 )
かつ
R3 / ∥(h1,h2,…,hn)∥2 → 0 ( ∥(h1,h2,…,hn)∥→ 0 )
が満たされる。
したがって、ここでは、
仮定Q1「grad f (a1,a2,…,an)=(0,0,…,0)」より、
f (a1+h1,a2+h2,…,an+hn)- f (a1,a2,…,an)=(1/2)Q(h1,h2,…,hn)+R3 …I-(1)
かつ
R3 → 0 ( ∥(h1,h2,…,hn)∥→ 0 ) …I-(2)
かつ
R3 / ∥(h1,h2,…,hn)∥2 → 0 ( ∥(h1,h2,…,hn)∥→ 0 ) …I-(3)
が満たされる。
Ⅱ.
任意の非零n次元数ベクトル(h1,h2,…,hn)≠(0,0,…,0)に対して、
Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2
を、(h1,h2,…,hn)の関数としてみると、
Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 の最小値Lが存在し[∵下記理由]、
仮定Q2より、
L>0
を満たす。
つまり、
(∀(h1,h2,…,hn) )( (h1,h2,…,hn)≠(0,0,…,0) ⇒ Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2≧L>0)
なお、
ノルムの定義より、
(h1,h2,…,hn)=(0,0,…,0) ⇔ ∥(h1,h2,…,hn)∥=0
だから、
(∀(h1,h2,…,hn) )( ∥(h1,h2,…,hn)∥≠0 ⇒ Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2≧L>0)
と言っても同じことである。
* * * * * *
別様に書くと、
『Rn上の点集合』
D={(h1,h2,…,hn)∈Rn|(h1,h2,…,hn)≠(0,0,…,0)}={(h1,h2,…,hn)∈Rn|∥(h1,h2,…,hn)∥≠0} (∵ノルムの定義: (h1,h2,…,hn)=(0,0,…,0) ⇔ ∥(h1,h2,…,hn)∥=0 )
において、
Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 の最小値Lが存在し、L>0
つまり、
(∀(h1,h2,…,hn) ∈D)(Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2≧L>0)
* * * * * *
「Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2の最小値L」の存在証明:最大値最小値定理から。
Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2
={ 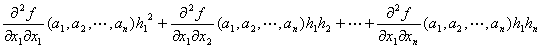
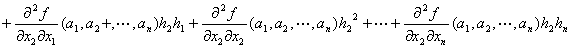
+…
:
…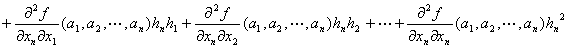 }/ ∥(h1,h2,…,hn)∥2 }/ ∥(h1,h2,…,hn)∥2
= 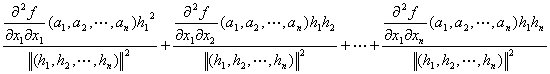
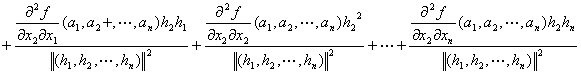
+…
:
…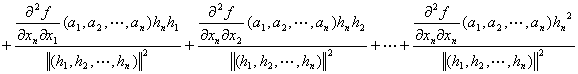
= 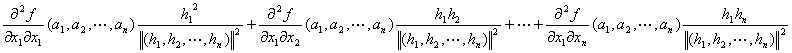
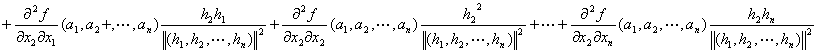
+…
:
…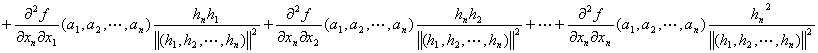
= 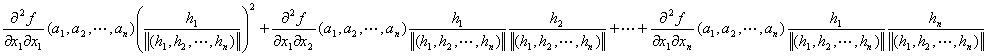
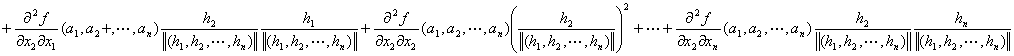
+…
:
…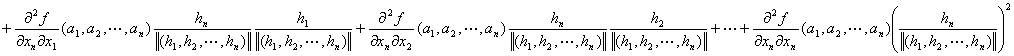
すると、Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 は、
n変数n値ベクトル値関数φ(h1,h2,…,hn)=(h1/ ∥(h1,h2,…,hn)∥ ,h2/ ∥(h1,h2,…,hn)∥ ,…,hn/ ∥(h1,h2,…,hn)∥ )
と
n変数実数値関数
ψ(h'1,h'2,…,h'n)=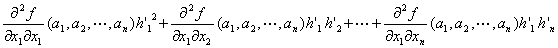
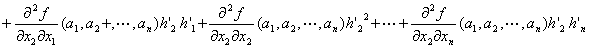
+…
:
…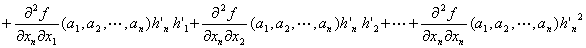
との合成関数
である。
つまり、
Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 =ψ( φ(h1,h2,…,hn) )
・φ(h1,h2,…,hn) とは、(h1,h2,…,hn) の単位ベクトル化に他ならないから、
任意の非零n次元数ベクトル(h1,h2,…,hn)≠(0,0,…,0)に対して、∥ φ(h1,h2,…,hn) ∥=1を満たす。
つまり、
定義域D={(h1,h2,…,hn)∈Rn|(h1,h2,…,hn)≠(0,0,…,0)}={(h1,h2,…,hn)∈Rn|∥(h1,h2,…,hn)∥≠0} に対して、
φ(h1,h2,…,hn)=(h1/ ∥(h1,h2,…,hn)∥ ,h2/ ∥(h1,h2,…,hn)∥ ,…,hn/ ∥(h1,h2,…,hn)∥ )の値域は、
{(h'1,h'2,…,h'n)∈Rn|∥(h'1,h'2,…,h'n)∥ =1 }
これは、要するに、原点を中心とする半径1のn次元球体の表面である。
・{(h'1,h'2,…,h'n)∈Rn|∥(h'1,h'2,…,h'n)∥ =1 } は、有界な閉集合であって、
ψ( h'1,h'2,…,h'n ) は、{(h'1,h'2,…,h'n)∈Rn|∥(h'1,h'2,…,h'n)∥ =1 } で連続(∵二次形式で定義される多変数関数は連続)。
したがって、最大値最小値定理より、
{(h'1,h'2,…,h'n)∈Rn|∥(h'1,h'2,…,h'n)∥ =1 } におけるψ( h'1,h'2,…,h'n )の最大値・最小値が存在する。
・上記二点をあわせて考えると、
合成関数 ψ( φ(h1,h2,…,hn) ) は、
D={(h1,h2,…,hn)∈Rn|(h1,h2,…,hn)≠(0,0,…,0)}={(h1,h2,…,hn)∈Rn|∥(h1,h2,…,hn)∥≠0} において、
最大値・最小値を有す
と結論できる。
Ⅲ. [ I-(3)を分析、Ⅱに統合 ]
・I-(3)「 R3 / ∥(h1,h2,…,hn)∥2 → 0 ( ∥(h1,h2,…,hn)∥→ 0 ) 」
を、極限の定義に遡って書き下すと、
(∀ε>0)(∃δ>0)(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ | R3/∥(h1,h2,…,hn)∥2|<ε )
除外近傍の概念を使うと、
( ∀ε>0 ) ( ∃δ>0 ) (∀(h1,h2,…,hn)∈Rn )( ∥(h1,h2,…,hn)∥∈ U*δ(0)⇒ R3/∥(h1,h2,…,hn)∥2 ∈ Uε(0) )
・だから、Ⅱで出てきた
「Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 の {(h1,h2,…,hn)∈Rn|∥(h1,h2,…,hn)∥≠0}における最小値」L
から作った正値 L/2 を、εの具体的な値としても、上記命題は成り立つ。
ε=L/2とすると、上記命題は、以下のようになる。
「ε=L/2にたいして、ある実数δ>0が存在し、
(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ | R3/∥(h1,h2,…,hn)∥2|<ε=L/2 )
を満たす。」
除外近傍の概念を使うと、
「ε=L/2にたいして、ある実数δ>0が存在し、
(∀(h1,h2,…,hn)∈U*δ(0) )( R3/∥(h1,h2,…,hn)∥2 ∈ Uε=L/2(0) )
を満たす。」
・つまり、
Ⅱで出てきた「Q(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 の{(h1,h2,…,hn)∈Rn|∥(h1,h2,…,hn)∥≠0}における最小値」Lに対して、
(∀(h1,h2,…,hn)∈Rn)(0<∥(h1,h2,…,hn)∥<δ ⇒ -L/2< R3/∥(h1,h2,…,hn)∥2<L/2 )
を満たす正数δが存在するといえる。
(∃δ>0)(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ -L/2< R3/∥(h1,h2,…,hn)∥2<L/2 )
除外近傍の概念を使うと、
(∃δ>0)(∀(h1,h2,…,hn)∈U*δ(0)) ( R3/∥(h1,h2,…,hn)∥2 ∈ UL/2(0) )
Ⅳ [Ⅱ,I-(3)→Ⅲから、I-(1)右辺への示唆]
δを、「『Ⅱで出てきたL』に対して、Ⅲで存在が示された」正数δであるとする。
Ⅱ,Ⅲより、
(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ (1/2)Q(h1,h2,…,hn) /∥(h1,h2,…,hn)∥2+R3/∥(h1,h2,…,hn)∥2 ≧ L/2 +R3/∥(h1,h2,…,hn)∥2 >0 )
ということは、不等式の最左辺・最右辺に∥(h1,h2,…,hn))∥2 (>0)をかけて、
(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ (1/2)Q(h1,h2,…,hn)+R3 >0 )
とできる。
つまり、
Ⅲで存在が示された正数δをつかった(h1,h2,…,hn)の範囲に対する制限「0<∥(h1,h2,…,hn)∥<δ」
を満たす限りで任意の(h1,h2,…,hn)に対して、
(1/2)Q(h1,h2,…,hn)+R3 >0
が満たされる。
除外近傍の概念を使って表現すると、(∀(h1,h2,…,hn)∈U*δ(0)) ( (1/2)Q(h1,h2,…,hn)+R3 >0 )
V. 結論
δを、「『Ⅱで出てきたL』に対して、Ⅲで存在が示された」正数δであるとする。
I-(1)とⅣより、
(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ f (a1+h1,a2+h2,…,an+hn)- f (a1,a2,…,an) =(1/2)Q(h1,h2,…,hn)+R3 >0 )
ということは、不等式の最左辺・最右辺だけに着目すると、
(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ f (a1+h1,a2+h2,…,an+hn) > f (a1,a2,…,an) )
つまり、
Ⅲで存在が示された正数δをつかった(h1,h2,…,hn)の範囲に対する制限「0<∥(h1,h2,…,hn)∥<δ」
を満たす限りで任意の(h1,h2,…,hn)に対して、
f (a1+h1,a2+h2,…,an+hn) > f (a1,a2,…,an)
が成立する。
以上を、
除外近傍の概念を使って表現すると、
「『Ⅱで出てきたL』に対して、Ⅲで存在が示された」正数δに対して、
(∀(h1,h2,…,hn)∈U*δ(0)) ( f (a1+h1,a2+h2,…,an+hn)>f (a1,a2,…,an) )
よって、仮定Q1,Q2のもとで、
(∃δ>0)(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ f (a1+h1,a2+h2,…,an+hn) > f (a1,a2,…,an) )
ないし
(∃δ>0) (∀(h1,h2,…,hn)∈U*δ(0)) ( f (a1+h1,a2+h2,…,an+hn)>f (a1,a2,…,an) )
が示されたことになる。
(a1+h1,a2+h2,…,an+hn)を(x1,x2,…,xn)と書くと、上記命題は、
(∃δ>0)(∀(x1,x2,…,xn)∈Rn )(0<∥(x1,x2,…,xn)-(a1,a2,…,an)∥<δ ⇒ f (x1,x2,…,xn) > f (a1,a2,…,an) )
ないし
(∃δ>0) (∀(x1,x2,…,xn)∈ U*δ(a1,a2,…,an)) (f (x1,x2,…,xn)>f (a1,a2,…,an) )
となるから、
仮定Q1,Q2のもとで、
点A=(a1,a2,…,an)は、f の狭義の極小点である。
|
|
証明
|
[条件R⇒
「n変数実数値関数fは点(a1,a2,…,an)で狭義極小」]
仮定R1: grad f (a1,a2,…,an)=(0,0,…,0)
仮定R2: 任意のn次元数ベクトル (h1,h2,…,hn)≠(0,0,…,0)に対して、
二次形式 (h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) >0
Ⅰ.
テイラー展開の公式によって、
f (a1+h1,a2+h2,…,an+hn)= f (a1,a2,…,an)+gradf(a1,a2,…,an)・(h1,h2,…,hn)+(1/2) (h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn)+R3
とおくと、
R3 → 0 ( ∥(h1,h2,…,hn)∥→ 0 )
かつ
R3 / ∥(h1,h2,…,hn)∥2 → 0 ( ∥(h1,h2,…,hn)∥→ 0 )
が満たされる。
したがって、ここでは、
仮定R1「grad f (a1,a2,…,an)=(0,0,…,0)」より、
f (a1+h1,a2+h2,…,an+hn)- f (a1,a2,…,an)=(1/2) (h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn)+R3 …I-(1)
かつ
R3 → 0 ( ∥(h1,h2,…,hn)∥→ 0 ) …I-(2)
かつ
R3 / ∥(h1,h2,…,hn)∥2 → 0 ( ∥(h1,h2,…,hn)∥→ 0 ) …I-(3)
が満たされる。
Ⅱ.
任意の非零n次元数ベクトル(h1,h2,…,hn)≠(0,0,…,0)に対して、
(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2
を、(h1,h2,…,hn)の関数としてみると、
(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 の最小値Lが存在し[∵下記理由]、
仮定R2より、
L>0
を満たす。
つまり、
(∀(h1,h2,…,hn) )( (h1,h2,…,hn)≠(0,0,…,0) ⇒ (h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2≧L>0)
なお、
ノルムの定義より、
(h1,h2,…,hn)=(0,0,…,0) ⇔ ∥(h1,h2,…,hn)∥=0
だから、
(∀(h1,h2,…,hn) )( ∥(h1,h2,…,hn)∥≠0 ⇒ (h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2≧L>0)
と言っても同じことである。
* * * * * *
別様に書くと、
『Rn上の点集合』
D={(h1,h2,…,hn)∈Rn|(h1,h2,…,hn)≠(0,0,…,0)}={(h1,h2,…,hn)∈Rn|∥(h1,h2,…,hn)∥≠0} (∵ノルムの定義: (h1,h2,…,hn)=(0,0,…,0) ⇔ ∥(h1,h2,…,hn)∥=0 )
において、
(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 の最小値Lが存在し、L>0
つまり、
(∀(h1,h2,…,hn) ∈D)((h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2≧L>0)
**********
[ (h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 の最小値Lの存在証明:最大値最小値定理から]
・(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 は、
n変数n値ベクトル値関数φ(h1,h2,…,hn)=(h1/ ∥(h1,h2,…,hn)∥ ,h2/ ∥(h1,h2,…,hn)∥ ,…,hn/ ∥(h1,h2,…,hn)∥ ) と
n変数実数値関数ψ(h'1,h'2,…,h'n)= (h'1,h'2,…,h'n) Hf(a1,a2,…,an) t(h'1,h'2,…,h'n)
との合成関数
である。
つまり、
(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 =ψ( φ(h1,h2,…,hn) )
なぜなら、
((h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn))/∥(h1,h2,…,hn)∥2
=((h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn))(1/∥(h1,h2,…,hn)∥)(1/∥(h1,h2,…,hn)∥)
=((h1,h2,…,hn)/∥(h1,h2,…,hn)∥)Hf(a1,a2,…,an)(t(h1,h2,…,hn)/∥(h1,h2,…,hn)∥) ∵行列積とスカラー積の混合式の性質
=((h1,h2,…,hn)/∥(h1,h2,…,hn)∥)Hf(a1,a2,…,an) t((h1,h2,…,hn)/∥(h1,h2,…,hn)∥) ∵行列のスカラー倍と転置の性質
したがって、φ(h1,h2,…,hn)=(h1/ ∥(h1,h2,…,hn)∥ ,h2/ ∥(h1,h2,…,hn)∥ ,…,hn/ ∥(h1,h2,…,hn)∥ ) 、ψ(h'1,h'2,…,h'n)= (h'1,h'2,…,h'n) Hf(a1,a2,…,an) t(h'1,h'2,…,h'n) とおくと、
(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 =(φ(h1,h2,…,hn))Hf(a1,a2,…,an) t(φ(h1,h2,…,hn))=Hf(a1,a2,…,an)[φ(h1,h2,…,hn)] =ψ( φ(h1,h2,…,hn) )
である。
・φ(h1,h2,…,hn) とは、(h1,h2,…,hn)の単位ベクトル化に他ならないから、
任意の非零n次元数ベクトル(h1,h2,…,hn)≠(0,0,…,0)に対して、∥ φ(h1,h2,…,hn) ∥=1を満たす。
つまり、
定義域D={(h1,h2,…,hn)∈Rn|(h1,h2,…,hn)≠(0,0,…,0)}={(h1,h2,…,hn)∈Rn|∥(h1,h2,…,hn)∥≠(0,0,…,0)} に対して、
φ(h1,h2,…,hn)=(h1,h2,…,hn)/∥(h1,h2,…,hn)∥の値域は、 {(h'1,h'2,…,h'n)∈Rn|∥(h'1,h'2,…,h'n)∥=1 } 。
これは、要するに、原点を中心とする半径1のn次元球体の表面である。
・{(h'1,h'2,…,h'n)∈Rn|∥(h'1,h'2,…,h'n)∥=1 } は、有界な閉集合であって、
ψ(h'1,h'2,…,h'n) は、{(h'1,h'2,…,h'n)∈Rn|∥(h'1,h'2,…,h'n)∥=1 } で連続(∵二次形式で定義される多変数関数は連続)。
したがって、最大値最小値定理より、
{(h'1,h'2,…,h'n)∈Rn|∥(h'1,h'2,…,h'n)∥=1 }におけるψ( h'1,h'2,…,h'n )の最大値・最小値が存在する。
・上記二点をあわせて考えると、
合成関数 ψ( φ(h1,h2,…,hn) ) は、
D={(h1,h2,…,hn)∈Rn|(h1,h2,…,hn)≠(0,0,…,0)}={(h1,h2,…,hn)∈Rn|∥(h1,h2,…,hn)∥≠(0,0,…,0)} において、
最大値・最小値を有す
と結論できる。
Ⅲ. [ I-(3)を分析、Ⅱに統合 ]
・I-(3)「 R3 / ∥(h1,h2,…,hn)∥2 → 0 ( ∥(h1,h2,…,hn)∥→ 0 ) 」
を、極限の定義に遡って書き下すと、
(∀ε>0)(∃δ>0)(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ | R3/∥(h1,h2,…,hn)∥2|<ε )
除外近傍の概念を使うと、
( ∀ε>0 ) ( ∃δ>0 ) (∀(h1,h2,…,hn)∈Rn )( ∥(h1,h2,…,hn)∥∈ U*δ(0)⇒ R3/∥(h1,h2,…,hn)∥2 ∈ Uε(0) )
・だから、Ⅱで出てきた
「(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn)/ ∥(h1,h2,…,hn)∥2 の {(h1,h2,…,hn)∈Rn|∥(h1,h2,…,hn)∥≠0}における最小値」L
から作った正値 L/2 を、εの具体的な値としても、上記命題は成り立つ。
ε=L/2とすると、上記命題は、以下のようになる。
「ε=L/2にたいして、ある実数δ>0が存在し、
(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ | R3/∥(h1,h2,…,hn)∥2|<ε=L/2 )
を満たす。」
除外近傍の概念を使うと、
「ε=L/2にたいして、ある実数δ>0が存在し、
(∀(h1,h2,…,hn)∈U*δ(0) )( R3/∥(h1,h2,…,hn)∥2 ∈ Uε=L/2(0) )
を満たす。」
・つまり、
Ⅱで出てきた「(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) / ∥(h1,h2,…,hn)∥2 の{(h1,h2,…,hn)∈Rn|∥(h1,h2,…,hn)∥≠0}における最小値」Lに対して、
(∀(h1,h2,…,hn)∈Rn)(0<∥(h1,h2,…,hn)∥<δ ⇒ -L/2< R3/∥(h1,h2,…,hn)∥2<L/2 )
を満たす正数δが存在するといえる。
(∃δ>0)(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ -L/2< R3/∥(h1,h2,…,hn)∥2<L/2 )
除外近傍の概念を使うと、
(∃δ>0)(∀(h1,h2,…,hn)∈U*δ(0)) ( R3/∥(h1,h2,…,hn)∥2 ∈ UL/2(0) )
Ⅳ [Ⅱ,I-(3)→Ⅲから、I-(1)右辺への示唆]
δを、「『Ⅱで出てきたL』に対して、Ⅲで存在が示された」正数δであるとする。
Ⅱ,Ⅲより、
(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ (1/2)(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) /∥(h1,h2,…,hn)∥2+R3/∥(h1,h2,…,hn)∥2 ≧ L/2 +R3/∥(h1,h2,…,hn)∥2 >0 )
ということは、不等式の最左辺・最右辺に∥(h1,h2,…,hn))∥2 (>0)をかけて、
(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ (1/2)(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) +R3 >0 )
とできる。
つまり、
Ⅲで存在が示された正数δをつかった(h1,h2,…,hn)の範囲に対する制限「0<∥(h1,h2,…,hn)∥<δ」
を満たす限りで任意の(h1,h2,…,hn)に対して、
(1/2) (h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) +R3 >0
が満たされる。
除外近傍の概念を使って表現すると、(∀(h1,h2,…,hn)∈U*δ(0)) ( (1/2)(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) +R3 >0 )
V. 結論
δを、「『Ⅱで出てきたL』に対して、Ⅲで存在が示された」正数δであるとする。
I-(1)とⅣより、
(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ f (a1+h1,a2+h2,…,an+hn)- f (a1,a2,…,an) =(1/2)(h1,h2,…,hn) Hf(a1,a2,…,an) t(h1,h2,…,hn) +R3 >0 )
ということは、不等式の最左辺・最右辺だけに着目すると、
(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ f (a1+h1,a2+h2,…,an+hn) > f (a1,a2,…,an) )
つまり、
Ⅲで存在が示された正数δをつかった(h1,h2,…,hn)の範囲に対する制限「0<∥(h1,h2,…,hn)∥<δ」
を満たす限りで任意の(h1,h2,…,hn)に対して、
f (a1+h1,a2+h2,…,an+hn) > f (a1,a2,…,an)
が成立する。
以上を、
除外近傍の概念を使って表現すると、
「『Ⅱで出てきたL』に対して、Ⅲで存在が示された」正数δに対して、
(∀(h1,h2,…,hn)∈U*δ(0)) ( f (a1+h1,a2+h2,…,an+hn)>f (a1,a2,…,an) )
よって、仮定R1,R2のもとで、
(∃δ>0)(∀(h1,h2,…,hn)∈Rn )(0<∥(h1,h2,…,hn)∥<δ ⇒ f (a1+h1,a2+h2,…,an+hn) > f (a1,a2,…,an) )
ないし
(∃δ>0) (∀(h1,h2,…,hn)∈U*δ(0)) ( f (a1+h1,a2+h2,…,an+hn)>f (a1,a2,…,an) )
が示されたことになる。
(a1+h1,a2+h2,…,an+hn)を(x1,x2,…,xn)と書くと、上記命題は、
(∃δ>0)(∀(x1,x2,…,xn)∈Rn )(0<∥(x1,x2,…,xn)-(a1,a2,…,an)∥<δ ⇒ f (x1,x2,…,xn) > f (a1,a2,…,an) )
ないし
(∃δ>0) (∀(x1,x2,…,xn)∈ U*δ(a1,a2,…,an)) (f (x1,x2,…,xn)>f (a1,a2,…,an) )
となるから、
仮定R1,R2のもとで、
点A=(a1,a2,…,an)は、f の狭義の極小点である。
|
![]()
![]()
![]()