n変数関数の高次偏微分　　

　・定義：n変数関数の2階偏導関数・第2次偏導関数/第n次偏導関数・n階偏導関数・高階偏導関数/Cn級
　・偏微分の順序：定理/Youngの定理/Schwarzの定理/C n級関数のn回までの偏微分は偏微分の順序を換えても変わらない

　※n変数関数の微分関連ページ：偏微分/微分演算子/全微分/高階全微分/
　※高次偏微分関連ページ：ベクトル値関数の高階偏微分/ n変数関数の高階偏微分/2変数関数の高階偏微分/1変数関数の高階微分
　※高次全微分関連ページ： ベクトル値関数の高階全微分/ n変数関数の高階全微分/2変数関数の高階全微分/1変数関数の高階微分
　※n変数関数微分の応用：合成関数の微分/平均値定理･テイラーの定理/極値問題
　　　　　　　　　　　　　　陰関数定理/逆関数定理/ラグランジュ未定乗数法
　→文献・総目次　

定義：2階偏導関数・第2次偏導関数・交叉偏導関数　　


定義


・ n変数関数y=f (x1,x2,…,xn )の偏導関数に、
　さらにその偏導関数が存在するならば、
　それらを、2階偏導関数、第2次偏導関数などと呼ぶ。　
・はじめに偏微分したときと、次に偏微分したときとで、
　偏微分する変数が異なる場合、
　その2階偏導関数を、交叉偏導関数と呼ぶこともある[西村『経済数学早わかり』]。
・ n変数関数y=f (x1,x2,…,xn )の第2次(2階)偏導関数として、
　以下のn2通りを考えることができる。
　　（→これらを一定のパターンに並べたのが、Hesse行列）
　・type-1-1.まず、x1 に関して偏微分して、次もx1 に関して偏微分。
　　　y=f (x1,x2,…,xn )のx1に関する偏導関数 f x1 (x1,x2,…,xn)　を、
　　　さらにx1で偏微分して出てきた導関数　
　　　　
　　　（記法）
　　　　　f x1 x1 (x1,x2,…,xn)　　∂2f/∂x12　
　　　　　　
　　　　　
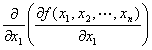
　・type-2-1. まず、x2 に関して偏微分して、次にx1 に関して偏微分。　
　　　y=f (x1,x2,…,xn )のx2に関する偏導関数 f x2 (x1,x2,…,xn)　を、
　　　x1で偏微分して出てきた導関数　
　　　　
　　　（記法）
　　　　　f x2 x1 (x1,x2,…,xn)　　∂2f /∂x1∂x2　
　　　　　
　　　　　
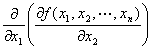
　　　*このように、別の変数で偏微分した2階偏導関数を、
　　　　交叉偏導関数と呼ぶ[西村『経済数学早わかり』]。
　：
　：
　・type-n-1. まず、xn に関して偏微分して、次にx1 に関して偏微分。
　　　y=f (x1,x2,…,xn )のx n に関する偏導関数 f xn (x1,x2,…,xn)　を、
　　　x1で偏微分して出てきた導関数　
　　　　
　　　（記法）
　　　　　f xn x1 (x1,x2,…,xn)　　∂2f /∂x1∂xn　
　　　　　
　　　　　　
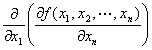
　　　*このように、別の変数で偏微分した2階偏導関数を、
　　　　交叉偏導関数と呼ぶ[西村『経済数学早わかり』]。

[文献]
岡田『経済学・経営学のための数学』1.6(p.48)
西村『経済数学早わかり』3章-3.1(p.119);
黒田『微分積分学』8.4.1 (p.297);
神谷浦井『経済学のための数学入門』6.3.1 (p. 224) ;
入谷久我『数理経済学入門』補足7.1(pp.164-5)。
杉浦『解析入門』Ⅱ§3 定義3(p.109);
小平『解析入門II』§6.4 (p.310) ;

※類概念：
　　1変数関数の第2次(2階)偏導関数
　　2変数関数の第2次(2階)偏導関数
　

　・type-1-2. まず、x1 に関して偏微分して、次にx2 に関して偏微分。　
　　　y=f (x1,x2,…,xn )のx1に関する偏導関数 f x1 (x1,x2,…,xn)　を、
　　　x2で偏微分して出てきた導関数　
　　　　
　　　（記法）
　　　　　f x1x2 (x1,x2,…,xn)　　∂2f /∂x2∂x1　
　　　　　
　　　　　
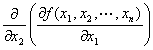
　　　*このように、別の変数で偏微分した2階偏導関数を、
　　　　交叉偏導関数と呼ぶ[西村『経済数学早わかり』]。
　・type-2-2. まず、x2 に関して偏微分して、次もx2 に関して偏微分。　
　　　y=f (x1,x2,…,xn )のx2に関する偏導関数 f x2 (x1,x2,…,xn)　を、
　　　さらにx2で偏微分して出てきた導関数　
　　　　
　　　（記法）
　　　　　f x2 x2 (x1,x2,…,xn)　　∂2f /∂x22　
　　　　　　
　　　　　
　：
　：
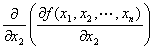
　・type-n-2. まず、xn に関して偏微分して、次にx2 に関して偏微分。　
　　　y=f (x1,x2,…,xn )のx n に関する偏導関数 f xn (x1,x2,…,xn)　を、
　　　x2で偏微分して出てきた導関数　
　　　　
　　　（記法）
　　　　　f xn x2 (x1,x2,…,xn)　　∂2f /∂x2∂xn　
　　　　　
　　　　　　
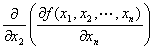
　　　*このように、別の変数で偏微分した2階偏導関数を、
　　　　交叉偏導関数と呼ぶ[西村『経済数学早わかり』]。
　：
　：
　・type-1-n. まず、x1 に関して偏微分して、次にxn に関して偏微分。　
　　　y=f (x1,x2,…,xn )のx1に関する偏導関数 f x1 (x1,x2,…,xn)　を、
　　　xnで偏微分して出てきた導関数　
　　　　
　　　（記法）
　　　　　f x1xn (x1,x2,…,xn)　　∂2f /∂xn∂x1　
　　　　　
　　　　　
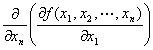
　　　*このように、別の変数で偏微分した2階偏導関数を、
　　　　交叉偏導関数と呼ぶ[西村『経済数学早わかり』]。
　・type-2-n. まず、x2 に関して偏微分して、次にxn に関して偏微分。　
　　　y=f (x1,x2,…,xn )のx2に関する偏導関数 f x2 (x1,x2,…,xn)　を、
　　　xn で偏微分して出てきた導関数　
　　　　
　　　（記法）
　　　　　f x2 xn (x1,x2,…,xn)　　∂2f /∂xn∂x2　
　　　　　
　　　　　
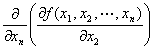
　　　*このように、別の変数で偏微分した2階偏導関数を、
　　　　交叉偏導関数と呼ぶ[西村『経済数学早わかり』]。
　：
　：
　・type-n-n. まず、xn に関して偏微分して、次もxn に関して偏微分。　
　　　y=f (x1,x2,…,xn )のx n に関する偏導関数 f xn (x1,x2,…,xn)　を、
　　　xn で偏微分して出てきた導関数　
　　　　
　　　（記法）
　　　　　f xn xn (x1,x2,…,xn)　　∂2f /∂xn2　
　　　　　　
　　　　　　

　 　

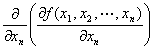
→[トピック一覧：n変数関数の高次の偏微分]
→総目次

　

定義：n階偏導関数・第n次偏導関数・高階偏導関数　　


定義


・2階以上の偏導関数を総称して高階偏導関数と呼ぶ。　
・ n変数関数y=f (x1,x2,…,xn )を、
　　　　k i1回、x i1 に関して偏微分（i1は1,2,…nのどれか）
　　　　k i2回、x i2に関して偏微分（i2は1,2,…nのどれか）　
　　　　　：　：　
　　　　k in回、x inに関して偏微分（i nは1,2,…nのどれか）　
　して得られた高階偏導関数は、
　(k1+ k2+…+ kn ) 階偏導関数ないし(k1+ k2+…+ kn )次導関数
　と呼ばれ、
　　　
　と表される。

[文献]
・岡田『経済学・経営学のための数学』1.6(p.48)
・黒田『微分積分学』8.4.2 (p.299);
・入谷久我『数理経済学入門』補足7.1(pp.164-5)。
・小平『解析入門II』§6.4 (p.310) ;

※類概念：
　　1変数関数の第n次(n階)偏導関数
　　2変数関数の高階偏導関数　
　 　

→[トピック一覧：n変数関数の高次の偏微分]
→総目次

　

定義：C k級　Function of Class C k　　


定義


n変数関数y=f (x1,x2,…,xn )が
「D上でk回連続微分可能」
ないし
「 D上で C k級 function of class C-k 」であるとは、　
f (x1,x2,…,xn )が領域D上でn階までのあらゆる偏導関数をもち、
それらがすべてD上で連続であることをいう。

[文献]
・岡田『経済学・経営学のための数学』1.6(p.48)
・黒田『微分積分学』8.4.2 (p.300);
・杉浦『解析入門』Ⅱ§3 定義4(p.111);
・小平『解析入門II』§6.4 (p.312) ;

※類概念：1変数関数のC n級/2変数関数のCn級

※

全微分可能との関係、偏微分の順序との関係


→[トピック一覧：n変数関数の高次の偏微分]
→総目次

　

偏微分の順序　
　

n変数関数y=f (x1,x2,…,xn )に、
2階偏導関数f x y , f yx　がともに存在したとしても
一致するとは限らない。　
では、
一致するための十分条件とは？



定理　
　

ある領域Dにおいて
 n変数関数y=f (x1,x2,…,xn )の偏導関数 f x , f y、2階偏導関数 f x y , f yx が存在して、
f x y (x1,x2,…,xn) , f yx (x1,x2,…,xn)　が連続
ならば、　　
f x y (x1,x2,…,xn) ＝ f yx (x1,x2,…,xn) 　が成り立つ


[文献]
小平『解析入門II』定理6.23(pp.311);

Youngの定理　
　


領域Dにおいて
 n変数関数y=f (x1,x2,…,xn )の偏導関数 f x , f y が存在して（全）微分可能
ならば、　
f x y (x1,x2,…,xn) ＝ f yx (x1,x2,…,xn) 　が成り立つ。　


[文献]
小平『解析入門II』定理6.24(pp.312);

Schwarzの定理　
　


ある領域Dにおいて
 n変数関数y=f (x1,x2,…,xn )の偏導関数f x , f y ,2階偏導関数 f x yが存在して、　
　　f x yが連続ならば　　
2階偏導関数f y xも存在して、
　　f x y (x1,x2,…,xn) ＝ f yx (x1,x2,…,xn) 　が成り立つ。


[文献]
黒田『微分積分学』定理8.13 (p.297);
杉浦『解析入門』Ⅱ§3定理3.2(p.109);

偏微分の順序についての結論　
　


以上の諸定理より、
C k級関数y=f (x1,x2,…,xn )について、
k回までの偏微分は
微分の順序を換えても変わらない。


[文献]
杉浦『解析入門』Ⅱ§3定理3.3(p.111);
黒田『微分積分学』系8.1:C2級(p.297);8.4.2:Ck級(p.299)。

→[トピック一覧：n変数関数の高次の偏微分]
→総目次

（reference）

西村和雄『経済数学早わかり』日本評論社、1982年、3章§4極値問題-定符号行列(p.138)。
黒田成俊『21世紀の数学1:微分積分学』共立出版株式会社、2002年、8.4高階偏導関数(p.297)。

『岩波数学辞典（第三版）』. 項目333　微分法[pp.983-986]

矢野健太郎・田代嘉宏『社会科学者のための基礎数学　改訂版』裳華房、pp.92-93.

小平邦彦『解析入門II』 (軽装版)岩波書店、2003年、pp.265-266。

高木貞治『解析概論　改訂第三版』岩波書店、1983年、p. 58.

和達三樹『理工系の数学入門コース1・微分積分』岩波書店、1988年、pp.118-119.

吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.162-163.

杉浦光夫『解析入門』岩波書店、1980年、pp.107-110. 　ただし、いきなり多次元。

高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.59-60。