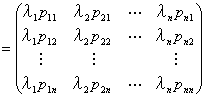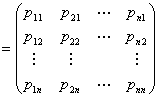・定義：固有ベクトル/固有値/固有多項式・特性多項式/固有方程式・特性方程式/特性根　
・定義：対角化可能
・定理：相異なる固有値に対する固有ベクトルは一次独立/固有値は特性根に一致する
　　　　対角行列の固有値・固有ベクトル/対角行列であるための必要十分条件―固有値固有ベクトルの観点
　　　　相似な行列の固有値は同一
・定理：対角化可能な行列の固有値固有ベクトル/行列対角化可能の条件−固有ベクトルの観点/行列対角化可能の条件−固有値の観点
・定理：実対称行列の固有値固有ベクトル/実対称行列の固有ベクトルの直交性/実対称行列の対角化　

※固有値問題関連ページ：実n次元数ベクトル空間上の一次変換の固有値問題/実ベクトル空間上の一次変換の固有値問題
※線形代数目次・総目次

定義

「実数λは
　　　『n次正方行列Aの(実)固有値eigenvalue』であり、
　実n次元数ベクトルxは
　　　『固有値λに属する/対応する/に対する固有ベクトルeigenvector』である」
とは、
n次正方行列Aにたいして、
　　実数λ, 実n次元数ベクトルxが、
　　　　　Ax=λx　かつ　x≠０　
　　を満たす
ことをいう。

・つまり、
　　（∃λ∈R）（∃x∈Rⁿ）（Ax=λx　かつ　x≠０）　
　となる場合に、
　このλ∈R, x∈Rⁿを、
　「固有値λに属する/対応する/に対する固有ベクトルeigenvector」
　と呼ぶ。

[文献]
・『岩波数学辞典』83行列L (p.222);
[文献−線型代数]
＊志賀『線型代数30講』27講(p.171):対角化との関連で;
＊木村『線形代数：数理科学の基礎』3.8(p.69):不変部分空間との関連で。
・斎藤『線形代数入門』5章§1(pp.131-8):体上のベクトル空間一般;
・佐武『線形代数学』�W§1(p.133):複素ベクトル空間・複素行列のケース;
[文献−数理経済・計量経済]
・Chiang,Fundamental Methods of Mathematical Economics,11.3(p.326)
＊西村『経済数学早わかり』2章§5.3(p.94):;
・岡田『経済学・経営学のための数学』定義2.6(p.94)
・久我入谷『数理経済学入門』4.3.2(p.103)
・岩田『経済分析のための統計的方法』12.5.1(p.300)
・佐和『回帰分析』2.3.1(p.30)
・戸田・山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.7(pp.102-5)

※n次正方行列Aの固有値・固有ベクトルは、
　n次正方行列Aによって定義される一次変換の固有値・固有ベクトル
　でもある。 [→一次変換の固有値・固有ベクトルと、一次変換の行列表現の固有値・固有ベクトルの関係]

・「正方行列Aの実固有値」は、
　存在しないこともあれば、
　一つしかないことも、
　複数存在することもある。
　正方行列Aの固有値の有無と個数は、
　正方行列Aに依存する。　

・おのおのの「正方行列Aの固有値」に対する固有ベクトルは、無数に存在する。
　実n次元数ベクトルxが「正方行列Aの固有値λに対する固有ベクトル」ならば、
　実n次元数ベクトルxの任意スカラー倍はどれも、
　「正方行列Aの固有値λの固有ベクトル」となるからである。
　なぜなら、
　　実n次元数ベクトルxが「正方行列Aの固有値λの固有ベクトル」ならば、
　　すなわち、「Ax=λx かつ x≠０」ならば、[仮定]　　　
　　　任意のa∈Rにたいして、
　　　A(ax)=a(A x)　　∵行列積とスカラー積の性質　　
　　　　　　= a(λx)　∵上記[仮定]より
　　　　　　=λ(ax)　

※固有値・固有ベクトルの求め方→特性根との一致　
※n次正方行列Aの固有値・固有ベクトルは、
　n次正方行列Aによって定義される一次変換の固有値・固有ベクトル　　
　でもある。
　　[→一次変換の固有値・固有ベクトルと、一次変換の行列表現の固有値・固有ベクトルの関係]　

活用例

２次形式の符号判定/多変数関数の極大の２階十分条件

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

[文献]
・『岩波数学辞典』83行列L (p.222);
[文献−線型代数]
＊志賀『線型代数30講』27講(pp.173-4);
・木村『線形代数：数理科学の基礎』3.8(p.69)。
・斎藤『線形代数入門』5章§1(pp.134-5):体上のベクトル空間一般;
・佐武『線形代数学』�W§1(pp.133-4):複素ベクトル空間・複素行列のケース;

[文献−数理経済]
＊西村『経済数学早わかり』2章§5.3(p.94):;
・岡田『経済学・経営学のための数学』2.6(p.102)
・岩田『経済分析のための統計的方法』12.5.1(p.300)

定義

n次正方行列Aの固有多項式・特性多項式characteristic polynomialとは、
　det ( A−λI_n )　
のこと。

定義

n次正方行列Aの固有方程式・特性方程式characteristic equationとは、
　det ( A−λI_n )=０　
のこと。

定義

n次正方行列Aの特性根characteristic rootとは、
　　　　固有方程式・特性方程式　det ( A−λI_n )=０　
の解・根のこと。

※n次正方行列Aの特性根は、n次正方行列Aの固有値に一致（→定理）　　

[文献−線型代数]
・斎藤『線形代数入門』5章§1[1.3](p.136):体上のベクトル空間一般:証明つき;

n次正方行列Aの(実) 固有値は、
n次正方行列Aの実特性根に一致する。

したがって、
n次正方行列Aの(実) 固有値と固有ベクトルを求めるためには、
まず、
n次正方行列Aの固有方程式・特性方程式を解いて、
n次正方行列Aの実特性根を求め、
そのうえで、
　　固有値・固有ベクトルの定義式　Ax=λx　
のλに、Aの実特性根を代入し、
固有ベクトルを求めればよい。

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

要旨

n次正方行列Aの相異なる(実)固有値に対応する固有ベクトルは、一次独立。

[文献]
・松坂『解析入門4』18.1-B-命題5 (p.87)：数ベクトル空間限定;
・志賀『線型代数30講』28講(p.177):R²上の一次変換;29講(p.183):固有空間:R²上の一次変換;
・斎藤『線形代数入門』5章§1[1.1](p.131):体上のベクトル空間上の一次変換:証明つき;
・戸田・山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.8.1(pp.108-9)2次正方行列の証明。

・西村『経済数学早わかり』2章§5.3定理5.2(p.95):証明つき;

※一次変換の固有値・固有ベクトルについての同じ定理。
※活用例：行列対角化の条件−固有値の観点の証明　

設定

R：実数体(実数をすべて集めた集合）　　
Rⁿ：実n次元数ベクトル空間。　
　　すなわち、Rⁿ=R×R×…×R＝{ ( v₁, v₂, …, v_n )｜v₁∈Rかつv₂∈Rかつ…かつv_n∈R }に、
　　　　　　　　ベクトルの加法とスカラー乗法を定義したもの。　
　　ただし、Rⁿに属すすべての実n次元数ベクトルは、 n次元縦ベクトルの形式で表されているものとする。
A：n次正方行列　

定理

k個の実数λ₁ ,λ₂ ,…,λ_kはそれぞれ異なる値　
　　　　　(∀i,j∈N) （(1≦i≦kかつ1≦j≦kかつi≠j　⇒　λ_i≠λ_j )　）　
かつ　　　
k個の実数λ₁ ,λ₂ ,…,λ_kは、どれもn次正方行列Aの(実)固有値　　
　　　　　(∀i∈N)（　(1≦i≦k　⇒　（∃x_i∈Rⁿ）（ Ax_i=λ_I x_i　かつ　x_I≠０） )　）　
ならば　　　
k個の実n次元数ベクトル　　　
　・『n次正方行列Aの(実)固有値』λ₁に対応する固有ベクトルx₁　
　・『n次正方行列Aの(実)固有値』λ₂に対応する固有ベクトルx₂　
　：　　　　　　　　　　　　　　：　　　　　　　　　　　　：　
　・『n次正方行列Aの(実)固有値』λ_kに対応する固有ベクトルx_k　　　　
は、一次独立である。　　　

証明

松坂『解析入門4』18.1-B-命題5 (p.87):帰納法による証明。
斎藤『線形代数入門』5章§1[1.1](p.131):背理法による証明。

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

要旨

[命題1]
　実数λ₁,λ₂,…,λ_nは、「n次対角行列 diag(λ₁,λ₂,…,λ_n)の固有値」であり、
　基本ベクトルe₁は『固有値λ₁に対応する固有ベクトル』　
　基本ベクトルe₂は『固有値λ₂に対応する固有ベクトル』
　　　　　　　：　　　　　　：　
　基本ベクトルe_nは『固有値λ_nに対応する固有ベクトル』
　である。

[命題2]
　実数λ₁,λ₂,…,λ_nが、「n次正方行列Bの固有値」であり、
　基本ベクトルe₁は『n次正方行列Bの固有値λ₁に対応する固有ベクトル』　
　基本ベクトルe₂は『n次正方行列Bの固有値λ₂に対応する固有ベクトル』
　　　　　　　：　　　　　　：　
　基本ベクトルe_nは『n次正方行列Bの固有値λ_nに対応する固有ベクトル』
　であるならば、
　n次正方行列Bは、n次対角行列 diag(λ₁,λ₂,…,λ_n)である。
　

[文献]
・松坂『解析入門4』18.1-C (pp.87-8);
※発展：定理「相似な実n次正方行列は同じ固有値をもつ」とあわせて考えると、
　　　　n次対角行列 diag(λ₁,λ₂,…,λ_n) に相似である行列、
　　　　すなわち、対角化可能な行列の
　　　　固有値固有ベクトルも、把握できたことになる。
　　　　[→対角化可能な行列の固有値固有ベクトル]　　

詳論

[命題1]
(1)
実数λ₁, 基本ベクトルe₁は、実n次対角行列 diag(λ₁,λ₂,…,λ_n)に対して、
　　・ diag(λ₁,λ₂,…,λ_n) e₁　
　　　　　　　
　　　　=λ₁ e₁　
　かつ
　　・e₁≠０　
　を満たすので、
　実数λ₁ , 基本ベクトルe₁は、
　　「実n次対角行列 diag(λ₁,λ₂,…,λ_n)の『固有値』,『固有値λ₁に対応する固有ベクトル』」
　の定義を満たしている。　
(2)
実数λ₂, 基本ベクトルe₂は、実n次対角行列 diag(λ₁,λ₂,…,λ_n)に対して、
　　・ diag(λ₁,λ₂,…,λ_n) e₂　
　　　　　　
　　　　=λ₂ e₂　
　かつ
　　・e₂≠０　
　を満たすので、
　実数λ₂ , 基本ベクトルe₂は、
　　「実n次対角行列Aの『固有値』,『固有値λ₂に対応する固有ベクトル』」
　の定義を満たしている。
：
：
(n)

実数λ_n, 基本ベクトルe_nは、実n次対角行列 diag(λ₁,λ₂,…,λ_n)に対して、
　　・ diag(λ₁,λ₂,…,λ_n) e_n　
　　　　　
　　　　=λ_ne_n　
　かつ
　　・e_n≠０　
　を満たすので、
　実数λ_n , 基本ベクトルe_nは、
　　「実n次対角行列Aの『固有値』,『固有値λ_nに対応する固有ベクトル』」
　の定義を満たしている。

[命題2]
・「実数λ₁,λ₂,…,λ_nが、「n次正方行列Bの固有値」であり、
　　基本ベクトルe₁は『n次正方行列Bの固有値λ₁に対応する固有ベクトル』　
　　基本ベクトルe₂は『n次正方行列Bの固有値λ₂に対応する固有ベクトル』
　　　　　　　　：　　　　　　　　　　　　　：　
　　基本ベクトルe_nは『n次正方行列Bの固有値λ_nに対応する固有ベクトル』
　である」とは、
　　　　　　　Be₁=λ₁e₁　　
　　　　　　　Be₂=λ₂e₂　　
　　　　　　　：　　　：　
　　　　　　　Be_n=λ_ne_n　　
　が成り立つということを意味する。（∵固有値・固有ベクトルの定義）　
・　　　Be₁=λ₁e₁　
　　　　Be₂=λ₂e₂　
　　　　：　　：
　　　　Be_n=λ_ne_n　
　が成り立つならば、
　行列と基本ベクトルの積の性質から、　
　　　　Bの第1列＝Be₁=λ₁e₁＝λ₁^t( 1,0,…,0 )＝^t(λ₁,0,…,0 )　
　　　　Bの第2列＝Be₂=λ₂e₂＝λ₂^t(0,1,0,…,0 )＝^t(0,λ₂, 0,…,0)　
　　　　　　　：　　
　　　　Bの第n列＝Be_n =λ_n e_n＝λ_n ^t(0,…,0,1)＝^t(0,…,0,λ_n )　
・以上二点から、
　実数λ₁,λ₂,…,λ_nが、「n次正方行列Bの固有値」であり、
　基本ベクトルe₁は『n次正方行列Bの固有値λ₁に対応する固有ベクトル』　
　基本ベクトルe₂は『n次正方行列Bの固有値λ₂に対応する固有ベクトル』
　　　　　　　：　　　　　　：　
　基本ベクトルe_nは『n次正方行列Bの固有値λ_nに対応する固有ベクトル』
　であるならば、
　n次正方行列Bは、n次対角行列 diag(λ₁,λ₂,…,λ_n)になる。

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

概要

相似な実n次正方行列は、同じ固有値をもつ。

[文献]
・松坂『解析入門4』18.1-B命題4(p.86)：数ベクトル空間限定;
・永田『理系のための線形代数の基礎』定理5.1.4(p.133):複素n次元数ベクトル。固有多項式の一致を証明。その系として。

※発展：対角行列の固有値固有ベクトルとあわせて考えると、
　　　　n次対角行列 diag(λ₁,λ₂,…,λ_n) に相似である行列、
　　　　　　　　　　　　　　　すなわち、対角化可能な行列の
　　　　固有値固有ベクトルも、把握できたことになる。
　　　　[→対角化可能な行列の固有値固有ベクトル]　　

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

詳細

以下の命題Pが成り立つならば、命題Q,命題Rは同値である。
つまり、命題P ⇒ (命題Q⇔命題R)　　

命題P「実n次正方行列Aと実n次正方行列Bとは相似である」
　　　　　すなわち、
　　　　　　　B=P^−１APを満たす n次正則行列Pが存在する
命題Q「実数λは『n次正方行列Aの実固有値』であり、
　　　　　　実n次元数ベクトルxは『実固有値λに属する固有ベクトル』である」
　　　　　すなわち、
　　　　　　　　Ax=λx　かつ　x≠０　
命題R「実数λは『n次正方行列Bの実固有値』であり、
　　　　　　P^−１xは『実固有値λに属する固有ベクトル』である」　
　　　　　すなわち、
　　　　　　　B(P^−１x)=λ(P^−１x)　

証明

[命題P ⇒ (命題Q⇒命題R) ]　
命題Qで仮定された「n次正方行列Aの実固有値λに属する固有ベクトル」xと、
命題Pで存在すると仮定された n次正則行列P
をつかって、
実n次元数ベクトルx'=P^−１xを定義する。
この実n次元数ベクトルx'の定義式より、
　x = P x'　
である（両辺に対し、左からPをかけて、左辺右辺を入れ替えただけ）。
これを命題Qで仮定された
　　Ax=λx　
に代入すると、
　　A(Px')=λ(Px')　
この左辺に行列積の結合則を、右辺に行列積とスカラー積の性質を適用すると、
　　APx'=P (λx')　
と書き換えられる。
この等式が成り立つならば、
この等式の左辺に左からP^−１をかけたものと、この等式の右辺に左からP^−１をかけたもの
も等しくなるから
　P^−１AP x'=λx'　
が得られる。
これを、命題Pの実n次正方行列Bを用いて、言い表すと、B=P^−１APだから、
　Bx'=λx'　
ここで、われわれが勝手に定義した実n次元数ベクトルx' を、もとの記号P^−１xに戻すと、
　B(P^−１x)=λ(P^−１x)　
以上、命題P,命題Qが成り立つという仮定のもとで、命題Rの成立を示した。
[命題P ⇒ (命題R⇒命題Q) ]　
命題Rで仮定された
　　B(P^−１x)=λ(P^−１x)　
に、命題Pで仮定されたB=P^−１APを代入すると、　
　　P^−１AP (P^−１x)=λ(P^−１x)　
この左辺を、行列積の結合則をつかって書き換えると、
　　P^−１A(PP^−１)x=λ(P^−１x)　
　　P^−１Ax=λ(P^−１x)　
この右辺を行列積とスカラー積の性質を使って書き換えると、
　　P^−１Ax=P^−１ (λx)　
この等式が成り立つならば、
この等式の左辺に左からPをかけたものと、この等式の右辺に左からPをかけたもの
も等しくなるから
　　PP^−１Ax= P P^−１ (λx)　　
　　Ax=λx　　
以上、命題P,命題Rが成り立つという仮定のもとで、命題Qの成立を示した。
　

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

[文献]
・松坂『解析入門4』18.1-C (p.88)：数ベクトル空間限定;
・岡田『経済学・経営学のための数学』2.6 (p.100)
・志賀『線型代数30講』27講(p.170)
・永田『理系のための線形代数の基礎』5.1 (p.133):
・http://mathworld.wolfram.com/DiagonalizableMatrix.html
・戸田・山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.8.1(p.110)
・西村『経済数学早わかり』2章§5.3 (p.99);

・
※理論的には、一次変換に関する対角化可能の文脈のなかで、
　「実正方行列の対角化可能」を理解することが望ましい。
※発展事項：
　　・対角化可能な行列の固有値固有ベクトル
　　・行列対角化の条件−固有ベクトルの観点
　　・行列対角化の条件−固有値の観点

・「実n次正方行列Aは対角化可能」とは、
　　実n次正方行列Aが対角行列と相似であること
　　つまり、実n次正方行列Aに対して、
　　　　　　　　B=P^−１APを満たす
　　　　　　　　　　n次対角行列Bと n次正則行列Pが存在すること
をいう。
・「実n次正方行列Aは n次正則行列Pによって対角化可能」とは、
　　　　　　　　B=P^−１APを満たす
　　　　　　　　　　n次対角行列Bが存在すること　　　
をいう。
　* B=P^−１AP　⇔　 A= PBP^−１　だから、
　　「実n次正方行列Aは対角化可能」とは、
　　　実n次正方行列Aに対して、
　　　　A= PBP^−１を満たすn次対角行列Bと n次正則行列Pが存在すること
　　と定義しても、同じこと。　　　

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

要旨

命題T「実n次正方行列Aは、 n次正則行列P によって、対角行列 diag(λ₁,λ₂,…,λ_n)に対角化可能。
　　　　　すなわち、実n次正方行列Aに対して、
　　　　　　　　　　　 diag(λ₁,λ₂,…,λ_n)=P^−１APを満たす n次正則行列Pが存在する。」
が成り立つならば、
命題S「実数λ₁ ,λ₂ ,…,λ_nが、実n次正方行列Aの実固有値であって、
　　　　 n次正則行列Pの第1列p₁, 第2列p₂,…, 第n列p_n　は、
　　　　　　　　『実n次正方行列Aの固有値λ₁,λ₂,…,λ_nに対応する固有ベクトル』となる」
　　　　　　　　　　　Ap₁ ＝λ₁ p₁　
　　　　　　　　　　　Ap₂ ＝λ₂ p₂　
　　　　　　　　　　　　：　　：
　　　　　　　　　　　Ap_n ＝λ_n p_n　
が成り立つ。
※固有値λ₁ ,λ₂ ,…,λ_nのなかに等しいものが存在するケースであれ、
　固有値λ₁ ,λ₂ ,…,λ_nが全て異なるケースであれ、
　この定理は成り立つ。
※この定理の逆は成り立つとは限らない。
　この定理の逆を成り立たせるには、固有値λ₁ ,λ₂ ,…,λ_nが全て異なるケースに限定しなければならない。
　→行列の対角化の十分条件　　

[文献]
・松坂『解析入門4』18.1-C定理1 (p.88)定理2 (p.89)：数ベクトル空間限定;
・草場『線型代数』4.2(pp.100-1)
・岩田『経済分析のための統計的方法』定理12.17(p.303)
※行列対角化の条件−固有ベクトルの観点/行列対角化の条件−固有値の観点　
※一次変換が対角化可能となるための必要十分条件　

証明

[命題T⇒命題S]
(step1)　対角行列の固有値・固有ベクトル
　定理「対角行列の固有値・固有ベクトル」より、
　実数λ₁,λ₂,…,λ_nは、対角行列 diag(λ₁,λ₂,…,λ_n) の固有値であり、
　基本ベクトルe₁は『固有値λ₁に対応する固有ベクトル』
　基本ベクトルe₂は『固有値λ₂に対応する固有ベクトル』
　　　　　　　：　　　　　　：　
　基本ベクトルe_nは『固有値λ_nに対応する固有ベクトル』
　である。
　すなわち、e₁, e₂, …, e_nを「基本ベクトルの縦ベクトル」としたとき、　
　　 diag(λ₁,λ₂,…,λ_n) e₁＝λ₁ e₁　
　　 diag(λ₁,λ₂,…,λ_n) e₂＝λ₂ e₂　
　　　　　　：　　　　　　　：
　　 diag(λ₁,λ₂,…,λ_n) e_n＝λ_n e_n　

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

[文献]
・松坂『解析入門4』18.1-C定理1の証明の前半 (p.88)

※ここで利用した定理：対角行列の固有値・固有ベクトル/相似な行列の固有値の一致

(step 2) 　Aの固有値・固有ベクトルを、対角行列の固有値・固有ベクトルに還元
・対角化可能の定義より、
　命題T「実n次正方行列Aは、 n次正則行列P によって、対角行列 diag(λ₁,λ₂,…,λ_n)に対角化可能である」
　とは、
　「実n次正方行列Aが対角行列 diag(λ₁,λ₂,…,λ_n) と相似である」ということ、
　すなわち、　
　「実n次正方行列Aに対して、 diag(λ₁,λ₂,…,λ_n)=P^−１APを満たす n次正則行列Pが存在する」
　ということを意味する。
・だから、
　命題Tが成り立つならば、定理「相似な実正方行列の固有値の一致」が適用され、
　実n次正方行列Aの固有値は、対角行列 diag(λ₁,λ₂,…,λ_n) の固有値に一致し、
　実n次正方行列Aの固有ベクトルは、
　　　対角行列 diag(λ₁,λ₂,…,λ_n) の固有ベクトル（縦ベクトル）の左から n次正則行列Pをかけたものに等しくなる。
・したがって、
　命題Tが成り立つならば、
　(step 1)で「対角行列 diag(λ₁,λ₂,…,λ_n) の固有値」であると明らかにされた「n個の相異なる実数」λ₁,λ₂,…,λ_nは、
　　実n次正方行列Aの「n個の相異なる固有値」でもあり、
　(step 1)で「対角行列 diag(λ₁,λ₂,…,λ_n) の固有値λ₁,λ₂,…,λ_nに対応する固有ベクトル」であると明らかにされた
　　　基本ベクトルe₁, e₂, …, e_nの縦ベクトル　
　　の左から n次正則行列Pをかけてつくった　
　　　　　　　　Pe₁, Pe₂, …, Pe_n　
　　は、「実n次正方行列Aの固有値λ₁,λ₂,…,λ_nに対応する固有ベクトル」でもある。
　　すなわち、
　　A(Pe₁)＝λ₁(Pe₁)　
　　A(Pe₂)＝λ₂(Pe₂)　
　　　：
　　A(Pe_n)＝λ_n(Pe_n)　
・なお、Pe₁, Pe₂,…, Pe_n は、それぞれ、Ｐの第1列,Ｐの第2列,…,Ｐの第n列である。
　　　（→行列と基本ベクトルとの積）
(結論)
以上から、
命題T「n次正方行列Aは、 n次正則行列P によって、対角行列 diag(λ₁,λ₂,…,λ_n)に対角化可能である」ならば、
命題S「実数λ₁ ,λ₂ ,…,λ_nが、実n次正方行列Aの実固有値であって、
　　　　 n次正則行列Pの第1列p₁, 第2列p₂,…, 第n列p_n　は、
　　　　　　　　『実n次正方行列Aの固有値λ₁,λ₂,…,λ_nに対応する固有ベクトル』となる」
　　　　　　　Ap₁ ＝λ₁ p₁　
　　　　　　　Ap₂ ＝λ₂ p₂　
　　　　　　　　：　　：　　　　
　　　　　　　Ap_n ＝λ_n p_n　

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

要旨

以下の命題S,命題Tは同値。
命題S:「以下の2条件を満たすn個の実n次元数ベクトルp₁, p₂,…, p_n が存在する。　
　　　　[条件1]　n個の実n次元数ベクトルp₁, p₂,…, p_n は、実n次正方行列Aの固有ベクトルである。
　　　　　　　　　すなわち、
　　　　　　　　　・実n次正方行列Aと実n次元数ベクトルp₁に対して、ある実数λ₁ が存在して
　　　　　　　　　　　　　Ap₁ ＝λ₁ p₁　を満たす
　　　　　　　　　かつ　
　　　　　　　　　・実n次正方行列Aと実n次元数ベクトルp₂に対して、ある実数λ₂ が存在して
　　　　　　　　　　　　　Ap₂ ＝λ₂ p₂　を満たす
　　　　　　　　　かつ　
　　　　　　　　　：　
　　　　　　　　　かつ　
　　　　　　　　　・実n次正方行列Aと実n次元数ベクトルp_nに対して、ある実数λ_nが存在して
　　　　　　　　　　　　　Ap_n ＝λ_n p_n　を満たす
　　　　[条件2]　n個の実n次元数ベクトルp₁, p₂,…, p_n は一次独立である。　　
命題T:　「n次正方行列Aは、 n次正則行列P によって、対角行列 diag(λ₁,λ₂,…,λ_n)に対角化可能」
　　　　すなわち、
　　　　「実n次正方行列Aに対して、
　　　　　　 diag(λ₁,λ₂,…,λ_n)=P^−１APを満たす n次正則行列Pが存在する。」
※ここで、
　・命題Sのもとで、命題Tに登場する実n次正方行列Pの実在を示す例は、
　　　　　命題Sに登場するp₁, p₂,…, p_n を第1列,第2列,…,第n列とする実n次正方行列。　
　・命題Tのもとで、命題Sに登場する「n個の実n次元数ベクトルp₁, p₂,…, p_n 」の実在を示す例は、
　　　　　命題Tに登場した「 n次正則行列Pの第1列p₁, 第2列p₂,…, 第n列p_n」である。　

[文献]
・松坂『解析入門4』18.1-C定理1 (p.88)定理2 (p.89)：数ベクトル空間限定;
・志賀『線型代数30講』27講(pp.170-1):固有値がn個未満のケースの検討が必読。
・斎藤『線形代数入門』5章§1[1.2]'(p.133):体上のベクトル空間上の一次変換:証明つき;
・草場『線型代数』4.2(pp.102-5)
・西村『経済数学早わかり』2章§5.3 (p.99):証明つき;
・戸田・山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.8.1(pp.109-110) : 証明つき;。
・岡田『経済学・経営学のための数学』定理2.30(p.106)：証明つき。

※関連事項：
　　・対角化可能な行列の固有値固有ベクトル
　　・対角化可能となるための条件−固有値の観点　　
　　・一次変換が対角化可能となるための必要十分条件　

証明

[命題S⇒命題T]
ここでは、命題Sに表現された以下の仮定のもとで、考察を進める。
　　[仮定0]　p₁＝^t( p₁₁, p₁₂,…, p_1n ) , p₂＝^t( p₂₁, p₂₂,…, p_2n ) ,…, p_n＝^t( p_n1, p_n2,…, p_nn )　　
　　[仮定1] Ap₁ ＝λ₁ p₁　
　　　　　　Ap₂ ＝λ₂ p₂　
　　　　　　　：　　：　
　　　　　　Ap_n ＝λ_n p_n　
　　[仮定2]　n個の実n次元数ベクトルp₁, p₂,…, p_n は一次独立　
　

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

[文献]
・西村『経済数学早わかり』2章§5.3 (p.99):証明つき;
・戸田・山田『計量経済学の基礎：統計的手法の理論とプログラミング』2.8.1(pp.109-110) :基底や一次変換を持ち出さず、行列計算の枠内で示しているのが特徴的。西村の論法を踏襲。
・岡田『経済学・経営学のための数学』定理2.30(p.106)：証明つき-西村を踏襲。
・松坂『解析入門4』18.1-C定理2 (p.89)：数ベクトル空間限定;
・志賀『線型代数30講』27-30講(pp.170-193):固有値がn個未満のケースの検討が必読。

(step1―Pを定義)
・第1列をp₁, 第2列をp₂,…, 第n列を p_nとする実n次正方行列Pをつくる。
(step2―Pは正則)
・ [仮定2]が成り立つならば、step1で定義した実n次正方行列Pは正則行列となる。（∵正則行列になるための必要十分条件）
(step3―AP=P diag(λ₁,λ₂,…,λ_n) )
・[仮定0][仮定1]が成り立つならば、
　つまり、実数λ₁ ,λ₂ ,…,λ_nが、「実n次正方行列Aの実固有値」であって
　　　　　p₁＝^t( p₁₁, p₁₂,…, p_1n ) , p₂＝^t( p₂₁, p₂₂,…, p_2n ) ,…, p_n＝^t( p_n1, p_n2,…, p_nn )が
　　　　　　　『実n次正方行列Aの実固有値λ₁,λ₂,…,λ_nに対応する固有ベクトル』であるならば、
　　AP=P diag(λ₁,λ₂,…,λ_n)　である。
・なぜなら、
　行列積APの各列を書き出すと、　
　　　「APの第1列」＝「実行列Aと『実行列Pの第1列』との行列積」
　　　「APの第2列」＝「実行列Aと『実行列 Pの第2列』との行列積」
　　　　　　　：　　　　　　　　　　　　　　　　：
　　　「APの第n列」＝「実行列Aと『実行列 Pの第n列』との行列積」　
　step1より、『Pの第1列』がp₁, 『Pの第2列』がp₂,…, 『Pの第n列』がp_nであったから、
　　　「APの第1列」＝Ap₁
　　　「APの第2列」＝Ap₂
　　　　　　　　：　　　：　
　　　「APの第n列」＝Ap_n　　
　[仮定1]より、
　　　「APの第1列」＝Ap₁＝λ₁ p₁
　　　「APの第2列」＝Ap₂＝λ₂ p₂
　　　　　　　　：　　：　　　：
　　　「APの第n列」＝Ap_n＝λ_n p_n　
　[仮定0]をつかうと、　　
　　　「APの第1列」＝Ap₁＝λ₁ p₁＝^t(λ₁ p₁₁,λ₁ p₁₂,…,λ₁ p_1n )　　　
　　　「APの第2列」＝Ap₂＝λ₂ p₂＝^t(λ₂ p₂₁,λ₂ p₂₂,…,λ₂ p_2n )　　　
　　　　　　　　：　　：　　　：
　　　「APの第n列」＝Ap_n＝λ_n p_n＝^t(λ_n p_n1,λ_n p_n2,…,λ_n p_nn )　　　
　だから、
　　　AP　
　　　
　他方、
　　　P diag(λ₁,λ₂,…,λ_n)
　　　　
　　　　
　したがって、AP=P diag(λ₁,λ₂,…,λ_n)　となる。
(step4―P^−１AP= diag(λ₁,λ₂,…,λ_n) )
・[仮定0][仮定1] [仮定2]が成り立つならば、P^−１AP = diag(λ₁,λ₂,…,λ_n)　
・なぜなら、
　step3より、[仮定0][仮定1]が成り立つならば、AP=P diag(λ₁,λ₂,…,λ_n)　…(等式1)。
　step2より、[仮定2]が成り立つならば、Ｐは正則行列となって、P^−１が存在する。
　したがって、[仮定0][仮定1] [仮定2]が成り立つならば、
　等式1の両辺に、左からP^−１をかけて、次の等式を得られる。
　　　　P^−１AP = diag(λ₁,λ₂,…,λ_n)　
(step5―結論)　
　「対角化可能」という語の定義より、
　「　P^−１AP = diag(λ₁,λ₂,…,λ_n)　」が成立することは、
　「　Aは、 n次正則行列P によって、対角行列 diag(λ₁,λ₂,…,λ_n)に対角化可能」と言い表せる。
　したがって、step4より、
　[仮定0][仮定1] [仮定2]が成り立つならば、
　命題T「n次正方行列Aは、 n次正則行列P によって、対角行列 diag(λ₁,λ₂,…,λ_n)に対角化可能」
　が成立する
　といってよい。

証明

[命題T⇒命題S]
・命題T「n次正方行列Aは、 n次正則行列P によって、対角行列 diag(λ₁,λ₂,…,λ_n)に対角化可能」ならば、
　対角化可能な行列の固有値固有ベクトルより、
　「実数λ₁ ,λ₂ ,…,λ_nは、実n次正方行列Aの実固有値であって、
　　　　 n次正則行列Pの第1列p₁, 第2列p₂,…, 第n列p_n　は、
　　　　　　　　『実n次正方行列Aの固有値λ₁,λ₂,…,λ_nに対応する固有ベクトル』となる」
　　　　　　　　　　　Ap₁ ＝λ₁ p₁　
　　　　　　　　　　　Ap₂ ＝λ₂ p₂　
　　　　　　　　　　　　：　　：
　　　　　　　　　　　Ap_n ＝λ_n p_n　

[文献]
・松坂『解析入門4』18.1-C定理1の証明の前半 (p.88)

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

・一般に、 n次正則行列を構成するn個の列はベクトルとして一次独立であるから、
　命題Tに登場した n次正則行列P のの第1列p₁, 第2列p₂,…, 第n列p_n　は、一次独立。　
　　となる。　
・上記二点より、命題Tが成り立つならば、
　以下の2条件を満たすn個の実n次元数ベクトルp₁, p₂,…, p_n が存在することが示された。　
　　　　[条件1]　n個の実n次元数ベクトルp₁, p₂,…, p_n は、実n次正方行列Aの固有ベクトル。
　　　　[条件2]　n個の実n次元数ベクトルp₁, p₂,…, p_n は一次独立。
　このようなn個の実n次元数ベクトルp₁, p₂,…, p_n の実在を示す例は、
　命題Tに登場した n次正則行列P のの第1列p₁, 第2列p₂,…, 第n列p_n　である。　
　だから、命題T⇒命題Sである。

→[トピック一覧：固有ベクトル固有値]
→線形代数目次・総目次

要旨

以下の命題S,命題Tは同値。
命題S:　「n個の相異なる実数λ₁ ,λ₂ ,…,λ_nが、実n次正方行列Aの実固有値である。」
　　　　　すなわち、
　　　　　　　Ap₁ ＝λ₁ p₁　
　　　　　　　Ap₂ ＝λ₂ p₂　
　　　　　　　　：　　：　　　　
　　　　　　　Ap_n ＝λ_n p_n　
　　　　　　かつ　
　　　　　　　(∀i,j∈N) （(1≦i≦kかつ1≦j≦kかつi≠j　⇒　λ_i≠λ_j )　）　
命題T:　「n次正方行列Aは、 n次正則行列P によって、対角行列 diag(λ₁,λ₂,…,λ_n)に対角化可能であって、
　　　　　かつ
　　　　　対角行列 diag(λ₁,λ₂,…,λ_n)の対角成分λ₁ ,λ₂ ,…,λ_nは、n個の相異なる実数である」
　　　　すなわち、
　　　　「実n次正方行列Aに対して、
　　　　　　 diag(λ₁,λ₂,…,λ_n)=P^−１APを満たす n次正則行列Pが存在し、
　　　　　　かつ
　　　　　　対角行列 diag(λ₁,λ₂,…,λ_n)の対角成分λ₁ ,λ₂ ,…,λ_nは、n個の相異なる実数である」
したがって、
上記命題Sは、
命題Tから「λ₁ ,λ₂ ,…,λ_nは相異なる」という条件をはずした命題T'
　「n次正方行列Aは対角化可能」
の十分条件。