Rn:実n次元数ベクトル空間
+:実n次元数ベクトル空間Rnに定義されているベクトルの加法
スカラーに続けてベクトルを並べて書いたもの:
実n次元数ベクトル空間Rnに定められているスカラー乗法
v1,v2,…,vl:l個の実n次元数ベクトル。
具体的に書くと、
v1= ( v11, v12, …, v1n ) ただし、v11 , v12 , …, v1n ∈R
v2= ( v21, v22, …, v2n ) ただし、v21 , v22 , …, v2n ∈R
: :
vl= ( vl1, vl2, …, vln ) ただし、vl1 , vl2 , …, vln ∈R
したがって、v1 , v2 , …, vl ∈Rn 。
なお、個数lが有限個であることに注意。
a1, a2, …, al :スカラー。a1, a2, …, al ∈R
※実n次元数ベクトルの具体例:
・実2次元数ベクトルの線型独立/従属
―1個の実2次元数ベクトルの線型独立/従属
―2個の実2次元数ベクトルの線型独立/従属[図解付]
―3個以上の実2次元数ベクトルの線型独立/従属
[文献1]
佐武
『線形代数学』Ⅲ§1(p.86);
斎藤
『線形代数入門』第4章§3(p.99):
[文献2]
永田
『理系のための線形代数の基礎』
1.2(p.10);1.3(p.16);
布川谷野中山
『線形代数と凸解析』定理2.5(p.35);
入谷久我
『数理経済学入門』定義3.11(p.75)
二階堂
『経済のための線型代数』I§2(pp.20-21)
[文献3]
神谷
『経済学のための数学入門 』§3.1.3(p.108);[文献4]
柳井竹内
『射影行列・一般逆行列・特異値分解』 §1.2(pp.5-6);
草場
『線形代数』定義2.2(pp.54-5);
木村
『線形代数』1.4(p.18);3.1(pp.50-51);
高橋
『経済学とファイナンスのための数学』1.2Ⅲ定義1.2.2(p.10);
Chiang,
Fundamental Methods of Mathematical Economics 4.3 (pp.70-71) .
佐和
『回帰分析』2.1.2(p.17);
グリーン
『計量経済分析I』定義2.5(p.26);
矢野田代
『社会科学者のための基礎数学』2章§6(p.43). ;
戸田山田『計量経済学の基礎:統計的手法の理論とプログラミング』2.4.2(p.76)
問1
このl個の実n次元数ベクトルv1,v2,…,vlにたいして、
a1v1+a2v2+…+alvl=0
を満たすl個の実数a1, a2, …, al は存在するだろうか?
存在するとしたら、それは、どのような実数l個の組合せになるのだろうか?
1-1
このl個の実n次元数ベクトルv1,v2,…,vlにたいして、
a1v1+a2v2+…+alvl=0
を満たすl個の実数a1, a2, …, alは少なくとも一組は存在する。
このことを論理記号であらわせば、
(∀ v1,v2,…,vl ∈Rn )(∃a1, a2, …, al∈R)( a1v1+a2v2+…+alvl=0 )
・なぜ、そうなるのかといえば、
どのようにl個の実n次元数ベクトルv1,v2,…,vlを選んだとしても、
このl個の実n次元数ベクトルv1,v2,…,vlにたいして、
l個の実数a1=a2=…=al=0が、
a1v1+a2v2+…+alvl=0
を満たすからである。
∵実n次元数ベクトルのスカラー0倍は零ベクトル、
零ベクトルとのベクトル和の性質
1-2
どのようにl個の実n次元数ベクトルv1,v2,…,vlを選んだとしても、
このl個の実n次元数ベクトルv1,v2,…,vlにたいして、
a1v1+a2v2+…+alvl=0
を満たすl個の実数a1, a2, …, alとして、
a1=a2=…=al=0が、いつでも存在する。
これは、見方をかえれば、
どのようにl個の実n次元数ベクトルv1,v2,…,vlを選んだとしても、
このl個の実n次元数ベクトルv1,v2,…,vlにたいして、
a1v1+a2v2+…+alvl=0かつa1=a2=…=al=0
を満すl個の実数a1, a2, …, al
が、いつでも存在するということ。
つまり、
(∀v1,v2,…,vl∈Rn)
(∃a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)かつ(a1=a2=…=al=0))
問2
・このl個の実n次元数ベクトルv1,v2,…,vlにたいして、
a1v1+a2v2+…+alvl=0
を満たすl個の実数a1, a2, …, alの組合せとしては、
まず、a1=a2=…=al=0をあげることができる(∵前段)。
・では、
このl個の実n次元数ベクトルv1,v2,…,vlにたいして、
a1v1+a2v2+…+alvl=0
を満たすl個の実数a1, a2, …, al の組合せは、
(i) a1=a2=…=al=0だけであって、
a1=a2=…=al=0以外の組合せは存在しないのだろうか?
それとも、
(ii) a1=a2=…=al=0に加えて、a1=a2=…=al=0以外の組合せも存在するのだろうか?
・つまり、
このl個の実n次元数ベクトルv1,v2,…,vlにたいして、
「a1v1+a2v2+…+alvl=0を満たし、
かつ、a1=a2=…=al=0を満たさない
l個の実数a1, a2, …, al 」
は
(i) 存在しないのか、
(ii) 存在するのか。
・この問いを論理記号であらわせば、
与えられたl個の実n次元数ベクトルv1,v2,…,vlにたいして、
(i) ¬((∃a1, a2, …, al∈R)((a1v1+a2v2+…+alvl=0)かつ¬(a1=a2=…=al=0)))
であるのか、それとも、
(ii) (∃a1, a2, …, al∈R)((a1v1+a2v2+…+alvl=0)かつ¬(a1=a2=…=al=0))
であるのか。
2
l個の実n次元数ベクトルv1,v2,…,vlの選び方によって、
「a1v1+a2v2+…+alvl=0を満たし、
かつ、a1=a2=…=al=0を満たさない
l個の実数a1, a2, …, al 」
が
(i) 存在しない
こともあれば、
(ii) 存在する
こともある。
・(i) (ii) の2つのケースに重複はないので、
l個の実n次元数ベクトルv1,v2,…,vlは、(i) か(ii) のいずれかである。
・ということは、
(i) (ii) は、あらゆるl個の実n次元数ベクトルを、2つのケースに二分する分類軸として機能する。
(i)を一次独立ないし線形独立と呼び、 (ii) 一次従属ないし線形従属をとよぶ。
の
定義
l個の実n次元数ベクトルv1,v2,…,vlが一次独立・線形独立であるとは、
・「このl個の実n次元数ベクトルv1,v2,…,vlにたいして、
a1v1+a2v2+…+alvl=0
を満たすl個の実数a1, a2, …, al の組合せは、
a1=a2=…=al=0だけであって、a1=a2=…=al=0以外の組合せは存在しない」ということ
・つまり、
「この実n次元数ベクトルv1,v2,…,vlにたいして、
a1v1+a2v2+…+alvl=0を満たし、かつ、a1=a2=…=al=0を満たさない
l個の実数a1, a2, …, al は存在しない」ということ
・論理記号であらわせば、与えられたv1,v2,…,vl ∈Rnにたいして、
¬((∃a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)かつ¬(a1=a2=…=al=0)))
をいう。
(2) この定義は、次のように述べてもよい。
l個の実n次元数ベクトルv1,v2,…,vlが一次独立・線形独立であるとは、
・「この実n次元数ベクトルv1,v2,…,vlにたいして、どのようにl個の実数a1, a2, …, al をとっても、
a1v1+a2v2+…+alvl≠0となるか、あるいは、a1=a2=…=al=0となるか、しかない」
ということ。
・論理記号であらわせば、与えられたv1,v2,…,vl ∈Rnにたいして、
(∀a1,a2,…,al∈R)((a1v1+a2v2+…+alvl≠0)または(a1=a2=…=al=0))
ということ。
(3) この定義は、次のようにも述べてもよい。
l個の実n次元数ベクトルv1,v2,…,vlが一次独立・線形独立であるとは、
・「この実n次元数ベクトルv1,v2,…,vlにたいして、どのようにl個の実数a1, a2, …, al をとっても、
a1v1+a2v2+…+alvl=0ならば、a1=a2=…=al=0」
ということ。
・論理記号であらわせば、与えられたv1,v2,…,vl ∈Rnにたいして、
(∀a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0) ⇒ (a1=a2=…=al=0))
ということ。
(4) この3つの線形独立の定義が同じモノであることは、次のようにして確かめられる。
¬((∃a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)かつ¬(a1=a2=…=al=0)))
⇔ (∀a1,a2,…,al∈R)¬((a1v1+a2v2+…+alvl=0)かつ¬(a1=a2=…=al=0))
∵存在命題の否定は否定命題の全称命題に言いかえられる
⇔ (∀a1,a2,…,al∈R)(¬(a1v1+a2v2+…+alvl=0)または¬¬(a1=a2=…=al=0))
∵連言の否定は、否定命題の選言に言いかえられる
⇔ (∀a1,a2,…,al∈R)(¬(a1v1+a2v2+…+alvl=0)または(a1=a2=…=al=0))
∵命題の2重否定はもとの命題
⇔ (∀a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)⇒(a1=a2=…=al=0))
∵ならば⇒の定義 :「A⇒B」とは、「(¬A)またはB」のこと
の
定義
l個の実n次元数ベクトルv1,v2,…,vlが一 次従属・線形従属であるとは、
・「このl個の実n次元数ベクトルv1,v2,…,vlに たいして、
a1v1+a2v2+…+alvl=0
を満たすl個の実数a1, a2, …, al の組合せには、
a1=a2=…=al=0に加え て、a1=a2=…=al=0以外の組 合せもある」ということ
・つまり、
「a1v1+a2v2+…+alvl=0 を満たし、かつ、a1=a2=… =al=0を満たさない
l個の実数a1, a2, …, al が存在する」ということ
・論理記号であらわせば、
(∃a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)かつ¬(a1=a2=… =al=0))
ということ
をいう。
(2) この定義は、次のように述べてもよい。
l個の実n次元数ベクトルv1,v2,…,vlが一 次従属・線形従属であるとは、
・「この実n次元数ベクトルv1,v2,…,vlに たいして、
『a1v1+a2v2+…+alvl≠0 または a1=a2=… =al=0』
を満たさないl個の実数a1, a2, …, al が存在する」
ということ
・論理記号であらわせば、与えられたv1,v2,…,vl ∈Rnに たいして、
(∃a1,a2,…,al∈R)¬(¬(a1v1+a2v2+…+alvl=0)または(a1v1+a2v2+…+alvl=0))
ということ
をいう。
(3) この定義は、次のようにも述べてもよい。
l個の実n次元数ベクトルv1,v2,…,vlが一 次従属・線形従属であるとは、
・「この実n次元数ベクトルv1,v2,…,vlに たいして、
『a1v1+a2v2+…+alvl=0ならば、a1v1+a2v2+…+alvl=0』
を満たさないl個の実数a1, a2, …, al が存在する」
ということ
・論理記号であらわせば、与えられたv1,v2,…,vl ∈Rnに たいして、
(∃a1,a2,…,al∈R)¬((a1v1+a2v2+…+alvl=0) ⇒ (a1=a2=… =al=0))
ということ
をいう。
(4) この3つの線形従属の定義が同じモノであることは、次のようにして確かめられる。
(∃a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)かつ¬(a1=a2=… =al=0))
⇔(∃a1,a2,…,al∈R)¬(¬(a1v1+a2v2+…+alvl=0)または(a1=a2=… =al=0))
∵命題の2重否定はもとの命題、選言の否定と否定命題の連言は言い換え可能
⇔(∃a1,a2,…,al∈R)¬((a1v1+a2v2+…+alvl=0) ⇒ (a1=a2=… =al=0))
∵ならば⇒の定義 :「A⇒B」 とは、「(¬A)またはB」のこと
/独立
の
関係
「l個の実n次元数ベクトルv1,v2,…,vlが一次独立・線形独立である」ことの否定命題。
・「l個の実n次元数ベクトルv1,v2,…,vlが一次独立・線形独立である」は、
「l個の実n次元数ベクトルv1,v2,…,vlが一次従属・線形従属である」ことの否定命題。
・なぜなら、
「v1,v2,…,vlが一次独立・線形独立」は、
¬((∃a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)かつ¬(a1=a2=…=al=0)))
として、
「v1,v2,…,vlが一次従属・線形従属」は、
((∃a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)かつ¬(a1=a2=…=al=0)))
として、
定義されているのだから、明らか。
a1v1+a2v2+…+alvl= a1 ( v11, v12, …, v1n )+a2 ( v21, v22, …, v2n )+…+al ( vl1, vl2, …, vln )
= ( a1 v11, a1 v12, …, a1 v1n )+( a2 v21, a2 v22, …, a2 v2n )+…+( al vl1, al vl2, …, al vln ) ∵スカラー倍の定義
= ( a1 v11+ a2 v21+…+ al vl1 , a1 v12+ a2 v22+…+ al vl2 , …, a1 v1n+a2 v2n +…+al vln ) ∵ベクトル和の定義
であるから、
a1v1+a2v2+…+alvl=0とは、
a1,a2,…,alについての、次の斉一次連立方程式にほかならない
(v1,v2,…,vlは既定だから、その成分は与えられているのであって、未知数ではない。)。
┌v11a1+v21a2+…+vl1al =0
│v12a1+v22a2+…+vl2al =0
│ : : :
└v1na1+v2na2+…+vlnal =0
※この連立方程式は、行列積を使えば、次のようにも記述できる。
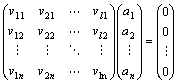
左辺は、
「1列目をv1の縦ベクトル、2列目をv2の縦ベクトル、…、l列目をvlの縦ベクトルとするn×l実行列」
と「a1,a2,…,alを縦に並べた縦ベクトル」との行列積であり、
右辺は、n次零ベクトルとなっている。
なお、これが満たされることは、左辺のn×l実行列が正則行列であることを意味するのだという。
[→木村『線形代数』1.4(p.18);3.1(p.51)]
したがって、
v1,v2,…,vlが一次独立であることの定義
「a1v1+a2v2+…+alvl=0を満たすl個の実数a1, a2, …, al の組合せは、
a1=a2=…=al=0だけであって、a1=a2=…=al=0以外の組合せは存在しない」
は、上記の斉一次連立方程式の解は、自明の解a1=a2=…=al=0だけだ、ということを意味している。
また、
v1,v2,…,vlが一次従属であることの定義
「a1v1+a2v2+…+alvl=0を満たすl個の実数a1, a2, …, alの組合せには、
a1=a2=…=al=0に加えて、a1=a2=…=al=0以外の組合せもある」
は、上記の斉一次連立方程式に、自明の解a1=a2=…=al=0以外の解が存在する、ということを意味する。
※上記の行列表現の話から、
v1,v2,…,vlが一次独立であることの定義は、
「1列目をv1の縦ベクトル、2列目をv2の縦ベクトル、…、l列目をvlの縦ベクトルとするn×l実行列」
が正則であることと同値[→木村『線形代数』1.4(p.18);3.1(p.51);佐武『線形代数学』Ⅲ§1定理2(p.90);]
※上記の行列表現の話から、
v1,v2,…,vlが一次従属であることの定義は、
「1列目をv1の縦ベクトル、2列目をv2の縦ベクトル、…、l列目をvlの縦ベクトルとするn×l実行列」
が特異行列であることと同値[→木村『線形代数』1.4(p.18);3.1(p.51)]
[文献2]にあげたテキストでは
「l個の実n次元数ベクトルv1,v2,…,vlが一次独立・線形独立である」の定義を、
「a1v1+a2v2+…+alvl=0 ⇒ a1=a2=…=al=0」
と定式化している。
他方、
「l個の実n次元数ベクトルv1,v2,…,vlが一次従属・線形従属である」は、
v1,v2,…,vlが一次独立でないこととして、定義している。
2.
ところが、ならばの真理値表・否定命題の真理値表をつかって、この定義を検討すると、妙なことになる。
| A | B | A⇒B | 「A⇒B」でない |
├───┼───┼─────┤──────────┤
| 真 | 真 | 真 | 偽 | ←1行目
| 真 | 偽 | 偽 | 真 | ←2行目
| 偽 | 真 | 真 | 偽 | ←3行目
| 偽 | 偽 | 真 | 偽 | ←4行目
「a1v1+a2v2+…+alvl=0」を命題A、「a1=a2=…=al=0」を命題Bと呼ぶことにする。
すると、
「l個の実n次元数ベクトルv1,v2,…,vlが一次独立・線形独立である」の上記の定義は、
「命題A⇒命題B」であり、
したがって、
「l個の実n次元数ベクトルv1,v2,…,vlが一次従属・線形従属である」の上記の定義は、
「『命題A⇒命題B』でない」である。
すると、真理値表より、
「『命題A⇒命題B』でない」
すなわち、「l個の実n次元数ベクトルv1,v2,…,vlが一次従属・線形従属である」
が成立するのは、
真理値表2行目のケース:
命題A「a1v1+a2v2+…+alvl=0」が成り立つが、命題B「a1=a2=…=al=0」が成り立たない
のときだけであって、
真理値表1行目のケース:
命題A「a1v1+a2v2+…+alvl=0」も、命題B「a1=a2=…=al=0」も成り立つ
のときは、
「『命題A⇒命題B』でない」
すなわち、「「l個の実n次元数ベクトルv1,v2,…,vlが一次従属・線形従属である」
は、成立しないことになる。
3.
ということは、「a1v1+a2v2+…+alvl=0 ⇒ a1=a2=…=al=0」の否定命題として一次従属を定義すると、
与えられたv1,v2,…,vlについて、
命題A「a1v1+a2v2+…+alvl=0」と命題B「a1=a2=…=al=0」が同時に成り立つケースでは、
このv1,v2,…,vlは一次従属でないと判定されることになる。
しかし、これはおかしい。
与えられたv1,v2,…,vlが一次独立であろうが、一次従属であろうが、
どんなv1,v2,…,vlについても、a1v1+a2v2+…+alvl=0とa1=a2=…=al=0とは同時に成立する。[→詳細]
すると、どんなv1,v2,…,vlも、一次従属には成り得ないことになってしまう。
4.
「v1,v2,…,vlが一次独立・線形独立」の定義の
「a1v1+a2v2+…+alvl=0 ⇒ a1=a2=…=al=0」という定式化は、
なにか必要な事項が省略されて、あいまいになっており、
そのせいで、この否定命題である「v1,v2,…,vlが一次・線形従属」の側で、
このような妙な事態が生じているのだと思われる。
5.
「v1,v2,…,vlが一次独立・線形独立」の定義を、
「a1v1+a2v2+…+alvl=0 ⇒ a1=a2=…=al=0」ではなく、
「(∀a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)⇒(a1=a2=…=al=0))」
つまり、「v1,v2,…,vlにたいして、どのように実数a1,a2,…,alの組合せをかえたとしても、
a1v1+a2v2+…+alvl=0ならば、a1=a2=…=al=0」
と定式化したうえで、
「v1,v2,…,vlが一次・線形従属」を、「v1,v2,…,vlが一次独立・線形独立」の否定命題として定義すれば、この問題は解消する。
「v1,v2,…,vlが一次独立・線形独立」を「(∀a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)⇒(a1=a2=…=al=0))」と定めたのだから、
その否定命題である「v1,v2,…,vlが一次・線形従属」は、
「¬((∀a1,a2,…,al∈R)((a1v1+a2v2+…+alvl=0)⇒(a1=a2=…=al=0)))」
つまり、「v1,v2,…,vlにたいして、
『どのように実数a1,a2,…,al の組合せをかえたとしても、
a1v1+a2v2+…+alvl=0ならば、a1=a2=…=al=0』
ということはない」
であるが、このような全称命題の否定は部分否定であるから否定命題の存在命題に言いかえられて、
「(∃a1,a2,…,al∈R)¬((a1v1+a2v2+…+alvl=0)⇒(a1=a2=…=al=0))」
つまり、「v1,v2,…,vlにたいして、
『a1v1+a2v2+…+alvl=0ならば、a1=a2=…=al=0』
を満たさない実数a1,a2,…,alの組合せが、少なくとも一つは、存在する」
としてよい。
したがって、このように定義すると、
v1,v2,…,vlが線形独立であるか線形従属であるかの違いは、
「a1v1+a2v2+…+alvl=0 ⇒ a1=a2=…=al=0」が成り立つか否かの違いではなく、
(i)実数a1,a2,…,al の値の組合せをどのようにかえたとしても、
「a1v1+a2v2+…+alvl=0 ⇒ a1=a2=…=al=0」が成り立つのか、
それとも、
(ii) 実数a1,a2,…,alの値の組合せをいろいろ変えてみると、a1,a2,…,alの値の組合せのなかには、
「a1v1+a2v2+…+alvl=0 ⇒ a1=a2=…=al=0」を成り立たせないものも、
少なくとも一つくらいは、あるといえるか、
という違いとなる。
6.
この定義だと、先の問題は、生じない。
確かに、
どのようにl個の実n次元数ベクトルv1, v2, …, vlを選んだとしても、
このl個の実n次元数ベクトルv1, v2, …, vlにたいして、
命題A「a1v1+a2v2+…+alvl=0」を成立させ、かつ命題B「a1=a2=…=al=0」も成立させる
実数 a1,a2,…,alの組合せ
は、常に存在する[→詳細]。
| A | B | A⇒B | 「A⇒B」でない |
├───┼───┼─────┤──────────┤
| 真 | 真 | 真 | 偽 | ←1行目
| 真 | 偽 | 偽 | 真 | ←2行目
| 偽 | 真 | 真 | 偽 | ←3行目
| 偽 | 偽 | 真 | 偽 | ←4行目
ということは、上記真理値表の1行目にあたり、
「『命題A(a1v1+a2v2+…+alvl=0) ⇒命題B(a1=a2=…=al=0)』でない」を成立させない
実数 a1,a2,…,al の組合せは、
どんなv1, v2, …, vlにも存在することになる。
しかし、ここでは、前と違って,「『命題A(a1v1+a2v2+…+alvl=0) ⇒命題B(a1=a2=…=al=0)』でない」は線形従属の定義ではない。
ここでの線形従属の定義は、
| 実数a1,a2,…,al の値の組合せをいろいろ変えてみると、a1,a2,…,al の値の組合せのなかには、
| 「『命題A(a1v1+a2v2+…+alvl=0) ⇒命題B(a1=a2=…=al=0)』でない」
| を成立させるものも、
| 少なくとも一つくらいはある
ということである。
したがって、
「『命題A(a1v1+a2v2+…+alvl=0) ⇒命題B(a1=a2=…=al=0)』でない」を成立させない実数a1,a2,…,al の組合せが存在するからといって、
線形従属の定義が満たされない、とは限らない。
「『命題A(a1v1+a2v2+…+alvl=0) ⇒命題B(a1=a2=…=al=0)』でない」を成立させない実数a1,a2,…,al の組合せは存在するが、
他に、「『命題A(a1v1+a2v2+…+alvl=0) ⇒命題B(a1=a2=…=al=0)』でない」を成立させる組合せが一つでも見つかれば、
線形従属であると判定してよいからである。
一般のベクトル空間における一次従属、体上の数ベクトル空間における一次従属