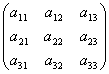定義：行列式 [数学についてのwebノート]

行列式の定義
・行列式の定義：行列式の公理的定義/公理的定義の同値条件/行列式の展開形(具体的定義)　・行列式の性質：列基本変形タイプ1に対する不変性/一次従属一次独立との関連/転置不変性/行列積の行列式
※小行列式/主小行列式　 ※線形代数目次・総目次

正方行列の行列式determinantの公理的定義・行列式写像

		[文献] ＊松坂『解析入門4』16.1-C～F (pp.33-41):体上の行列一般の行列式について公理的に定義。部分行列、小行列式は、16.2-E(p.51). ＊神谷浦井『経済学のための数学入門』§5.2.3～5.2.4(pp.170-181):体上の行列一般の行列式について公理的に定義。小行列式は、p.179; ・志賀『線形代数30講』22～23講(pp.138～148); ・木村『線形代数：数理科学の基礎』1.3(p.9): 公理的に定義。具体的な数値の入った行列ならば、この定義だけでも、行列式の値が計算できることも示されている。・二階堂『経済のための線型代数』I§3(pp.24-32):体上の行列一般の行列式について公理的に定義。小行列・小行列式はp.46 ・草場『線形代数』1.8(pp.26-28);
定義	「n次正方行列Aの行列式」　　　det A　　　｜A｜とは、 n次正方行列Aに対して実数を対応付ける写像　　　f : M_n(R)→R　　　（記号M_n(R)は、実数体上のn次全行列環を表す）であって、次の三要件を満たすもののことをいう。 [要件1: 単位行列] 　n次単位行列I_nに対して、　　　　f（ I_n ）=１　 [要件2: 交代性] 　n次正方行列 Aの二つの列を入れ替えて、　n次正方行列 A'をつくる[→列基本変形2]。　すると、f（A'）=－f（A）になる。　つまり、
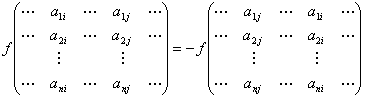
	[→この要件と同値な条件]
	[要件3: 多重線形性]
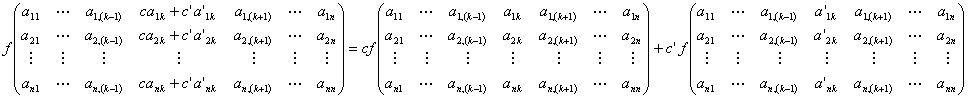
※	以上の要件を満たす写像は、下記の展開形だけであると、証明される。

→[トピック一覧：行列式]
→線形代数目次・総目次

行列式の交代性の同値条件

		[文献] ・松坂『解析入門4pp』16.1-C定理2(p.35). ・神谷浦井『経済学のための数学入門』定理5.2.1(p.172). ・志賀『線形代数30講』22講(p.140); ・二階堂『経済のための線型代数』I§3(p.28):体上の行列一般の行列式について公理的に定義。・草場『線形代数』1.7(p.25);
	行列式の定義の要件2は、次の条件と同値。要件2': 「n次正方行列 Aの列の中に、等しい列があれば、　　　　　　Aの行列式 detA=０」 [証明：行列式の定義の要件2 ⇒要件2'] 　・神谷浦井『経済学のための数学入門』定理5.2.1(p.172). 　・志賀『線形代数30講』22講(p.140) . 　・二階堂『経済のための線型代数』I§3(p.28). 　・草場『線形代数』1.7(p.25); [証明：要件2'⇒行列式の定義の要件2] 　・松坂『解析入門4』16.1-C定理2-a(pp.35). 　・志賀『線形代数30講』22講(p.140).

→[トピック一覧：行列式]
→線形代数目次・総目次

正方行列の行列式は、列基本変形type1に対して、不変。

		[文献] ・草場『線形代数』1.10(p.30); ・松坂『解析入門4』16.1-C定理2(pp.35). ・神谷浦井『経済学のための数学入門』定理5.2.1(p.172).
	n次正方行列 Aのある列をスカラー倍したものを、Aの他の列に加えて、 n次正方行列 A'をつくる[→列基本変形1]。　すると、detA=detA'になる。 ※なぜ？行列式の要件3（多重線形性）と行列式の要件2の同値条件から。　証明は下記参照。　　・松坂『解析入門4』16.1-C定理2(b)(pp.35-36). 　・草場『線形代数』1.10(2)(p.30); 　・神谷浦井『経済学のための数学入門』定理5.2.1-(2)(p.172).

→[トピック一覧：行列式]
→線形代数目次・総目次

正方行列の行列式と一次従属・一次独立

		[文献] ・松坂『解析入門4』16.1-C定理2-(c)(pp.35) :証明つき. ・二階堂『経済のための線型代数』I§3(p.28):証明つき。
	・n次正方行列 Aを構成する各列が一次従属ならば、detA=０・detA≠０ならば、n次正方行列Aを構成する各列は一次独立。

→[トピック一覧：行列式]
→線形代数目次・総目次

定義：正方行列の行列式determinantの展開形 (具体的定義)

		[文献-全般] ・『岩波数学辞典』84行列式A定義(p.224); [文献-線型代数] ・佐武『線型代数学』Ⅱ§2(p.47); ・斎藤『線型代数入門』3章§2(p.78); ・永田『理系のための線型代数の基礎』2.2(p.59); ・砂田『行列と行列式』§3.3a定義3.17 (p.105); [第(i,j)小行列式→定義3.35,p.114] ・志賀『線形代数30講』22～23講(pp.138～148); ・木村『線形代数：数理科学の基礎』1.3(p.11): ・草場『線形代数』定理1.5(p.28); [文献-解析] ・松坂『解析入門4』16.1-C～F (pp.33-41):体上の行列一般の行列式について公理的に定義。部分行列、小行列式は、16.2-E(p.51) [文献-数理経済] ・西村『経済数学早わかり』２章§2.3(pp.58-61).諸行列式は、5.1(p.86) ・神谷浦井『経済学のための数学入門』§5.2.3～5.2.4(pp.170-181) :体上の行列一般の行列式について公理的に定義。; ・二階堂『経済のための線型代数』I§3(pp.29-31)。小行列・小行列式はp.46 ・グリーン『計量経済分析』2.4.6(p.30):面積としての解釈を定義としてしまっている;小行列は、p.33
	[1次正方行列の行列式の展開形]
	1次正方行列　　　a₁₁ の行列式は、　　　a₁₁　と表される。
	[2次正方行列の行列式の展開形]
	2次正方行列　の行列式は、　a₁₁a₂₂－a₁₂a₂₁ と表される。
	[3次正方行列の行列式の展開形]
	3次正方行列　の行列式は、　a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₁₃a₂₁a₃₂－a₁₁a₂₃a₃₂－a₁₂a₂₁a₃₃－a₁₃a₂₂a₃₁ と表される。
	[n次正方行列の行列式の展開形]
	右記文献参照。
※	行列式であるための要件を満たすのは、上記の展開形だけである。 [証明] ・松坂『解析入門4』16.1-E～F (pp.38-41) ・志賀『線形代数30講』22～23講(pp.140～148); ・二階堂『経済のための線型代数』I§3(pp.29-31)。
※	PCでの行列式の計算・Excelをつかう場合　　　=MDETERM (範囲)　　　　　　＊範囲で行列を入力したセル範囲を指定。・Mathematicaをつかう場合　　　Det [ 行列 ]

→[トピック一覧：行列式]
→線形代数目次・総目次

行列式の転置不変性

定理	n次正方行列Aに対して、detA=det(^tA)。つまり、転置しても、行列式は変わらない。	[文献-線型代数] ・佐武『線型代数学』Ⅱ§2定理2(p. 49); ・斎藤『線型代数入門』3章§2定理2.1 (p.79); ・永田『理系のための線型代数の基礎』定理2.2.2(p.61); ・砂田『行列と行列式』§3.3b定理3.20 (p.106) ・志賀『線形代数30講』24講(pp.152～3); ・木村『線形代数：数理科学の基礎』1.4(p.17): ・草場『線形代数』1.9(p.29); [文献-解析] ・松坂『解析入門4』定理5 (p. 41) [文献-数理経済] ・西村『経済数学早わかり』定理2.1(p.61) ・神谷浦井『経済学のための数学入門』定理5.2.4(pp.179-180); ・二階堂『経済のための線型代数』I§3-5-[iii](p.35)。・グリーン『計量経済分析』2.4.6(p.33)
証明	行列式の展開形から。

→[トピック一覧：行列式]
→線形代数目次・総目次

行列積の行列式

	n次正方行列A,Bに対して、det(AB)=(detA) (detB)。	[文献-線型代数] ・佐武『線型代数学』Ⅱ§5定理8(p. 65); ・斎藤『線型代数入門』3章§2定理2.7 (p.82); ・永田『理系のための線型代数の基礎』定理2.2.9(p.66); ・砂田『行列と行列式』§3.3b定理3.29 (p.110) ・志賀『線形代数30講』24講(p.154); ・木村『線形代数：数理科学の基礎』1.4(p.18;22): ・草場『線形代数』1.10(4)(p.30); [文献-解析] ・松坂『解析入門4』16.2-c定理2 (p. 47) [文献-数理経済] ・西村『経済数学早わかり』定理2.4(p.70) ・神谷浦井『経済学のための数学入門』定理5.2.3(pp.177-8);

→[トピック一覧：行列式]
→線形代数目次・総目次

(reference)
日本数学会編集『岩波数学辞典（第三版）』岩波書店、1985年、項目210線形空間(pp.570-576)
線形代数のテキスト
ホフマン・クンツェ『線形代数学I』培風館、1976年、2.1ベクトル空間(pp.28-34)。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.3ベクトル空間(pp.14-6)。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§6ベクトル空間の公理化(p.115)。
砂田利一『現代数学への入門：行列と行列式』2003年、§5.1-b(p.155).
志賀浩二『数学30講シリーズ：線形代数30講』朝倉書店、1988年、13講ベクトル空間へ(p.83);14講ベクトル空間の例と基本概念(p.88)。
藤原毅夫『理工系の基礎数学2：線形代数』岩波書店、1996年、1.1ベクトルとベクトルの演算(p.4)、4.1線形空間と写像(p.91)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第2章§1行列の定義と演算(p.31);§3(p.46);§6(p.61)第４章§2線形空間(p.96):実線形空間･複素線形空間のみ;附録Ⅲ§2体(p.249)。

代数学のテキスト
本部均『新しい数学へのアプローチ5：新しい代数』共立出版、1969年、5.2-Aベクトル空間(p.132)。
酒井文雄『共立講座21世紀の数学8：環と体の理論』共立出版、1997年、1.6ベクトル空間(p.22)。

解析学のテキスト
杉浦光夫『解析入門I』東京大学出版会、1980年、I章§4(pp.33-4)

数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§3.1ベクトル空間とは何か(p.105)。
西村和雄『経済数学早わかり』日本評論社、1982年、２章線形代数§1ベクトル(pp.26-)。
Chiang, Fundamental Methods of Mathematical Economics: Third Edition, McGraw Hill,1984,1.
布川昊,谷野哲三,中山弘隆『線形代数と凸解析』コロナ社、1991年、2.4基底と次元(pp.36-41)。
高橋一『経済学とファイナンスのための数学』新世社、1999年、1.2Ⅲ定義1.2.2(p.10)。
二階堂副包『経済のための線型代数』培風館、1961年、I§1(pp.18-9)。

数理統計学のテキスト
William H. Greene（斯波・中妻・浅井訳）『経済学体系シリーズ：グリーン計量経済分析I：改訂4版』エコノミスト社、2000年、第２章行列代数2.2行列の用語(pp.10-12);2.3行列の算法(pp.12-21)。
岩田暁一『経済分析のための統計的方法(第2版)』東洋経済新報社、1983年、12.1行列の演算(pp.269-277);12.4.2逆行列(pp.294-5)。

→[トピック一覧：行列式]
→線形代数目次・総目次