設定
すなわち、
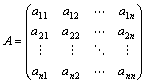
[
文献]・斎藤『線形代数入門』2章§2(p.43);
・藤原『線形代数』2.1(p.21) ;
・松坂『解析入門4』15.1-C (p. 6) ;
・戸田山田『計量経済学の基礎:統計的手法の理論とプログラミング』2.1.1(p.48)
定義
Aの対角線上にある成分a11, a22, …,annのこと。
n次正方行列 Aの非対角成分とは、
Aの対角線上にない成分aij (i≠j)のこと。
|
・定義: 対角成分・非対角成分/対角和・トレース・定義:対角行列/スカラー行列/クロネッカーのδ/単位行列/直交行列/ベキ等行列 |
|
※ 実行列関連ページ:実行列の定義/行列和・スカラー倍の定義/行列積の定義/行列積の性質/逆行列・正則行列・特異行列の定義/転置行列の性質/行列の代数系※線形代数目次・総目次 |
|
|
すなわち、 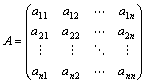 |
[ 文献]・斎藤『線形代数入門』2章§2(p.43); ・藤原『線形代数』2.1(p.21) ; ・松坂『解析入門4』15.1-C (p. 6) ; ・戸田山田『計量経済学の基礎:統計的手法の理論とプログラミング』2.1.1(p.48) |
|
定義 |
n次正方行列 Aの対角成分とは、 Aの対角線上にある成分a11, a22, …,annのこと。 n次正方行列 Aの非対角成分とは、 Aの対角線上にない成分aij (i≠j)のこと。 |
|
|
定義:対角和・跡・トレース trace・シュプールSpur |
||
|
|
A:R上のn次正方行列 すなわち、 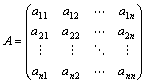 |
[ 文献]・藤原『線形代数』2.1(p.29) |
|
定義 |
n次正方行列 Aの対角和・跡・トレースtrace・シュプールSpurとは、 Aの対角成分の和a11+a22+…+annのこと。 (なお、上記の+は、実数体Rにおいて定義されている加法) |
|
|
記号 |
n次正方行列 Aの対角和・トレースは、記号「Tr A」などで表される。 | |
|
→ [トピック一覧:実数体上の正方行列に関する様々な定義]→ 線形代数目次・総目次 |
| diagonal matrix | ||
|
[ 文献]・『岩波数学辞典』83行列A(p.220); ・永田『理系のための線形代数の基礎』5.1(p.133); ・斎藤『線形代数入門』2章§2(p.43); ・藤原『線形代数』2.5(p.52); ・グリーン『計量経済分析』2.2行列の用語(p.12) ; ・戸田山田『計量経済学の基礎:統計的手法の理論とプログラミング』2.1.1(p.49) ・松坂『解析入門4』18.1-C (p.88):数ベクトル空間限定; |
||
|
対角行列 とは、すべての非対角成分が0である正方行列のことをいう。すなわち、  のこと。 対角行列  を、 diag(a11, a22,…, a n n) と表すこともある。 |
||
|
※ |
性質: 対角行列の固有値・固有ベクトル活用例:対角化可能 |
|
|
→ [トピック一覧:実数体上の正方行列に関する様々な定義]→ 線形代数目次・総目次 |
|
定義:スカラー行列 scalar matrix |
||
|
[ 文献]・『岩波数学辞典』83行列(p.220); ・斎藤『線形代数入門』2章§2(p.43); ・グリーン『計量経済分析』2.2(p.12) |
||
|
定義 |
スカラー行列 とは、すべての対角成分が等しい対角行列のこと、すなわち、すべての対角成分が等しく、なおかつ、すべての非対角成分が0である正方行列のことをいう。 すなわち、  のこと。 |
|
|
→ [トピック一覧:実数体上の正方行列に関する様々な定義]→ 線形代数目次・総目次 |
|
定義:クロネッカーのデルタ Kronecker's delata |
||
|
[ 文献]・『岩波数学辞典』83行列A(p.220); ・永田『理系のための線形代数の基礎』1.4(p.25); ・斎藤『線形代数入門』2章§1(p.35); ・藤原『線形代数』1.2(p.11) |
||
|
定義 |
次のように定義した δijを、クロネッカーのデルタと呼ぶ。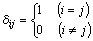 |
|
|
→ [トピック一覧:実数体上の正方行列に関する様々な定義]→ 線形代数目次・総目次 |
[yahoo:yoko] |
| unit matrix, identity matrix | ||
|
[ 文献]・『岩波数学辞典』83行列(p.220); ・永田『理系のための線形代数の基礎』1.4(p.26); ・斎藤『線形代数入門』2章§1(p.35); ・藤原『線形代数』2.1(p.27); ・グリーン『計量経済分析』2.2(p.12) ; ・戸田山田『計量経済学の基礎:統計的手法の理論とプログラミング』2.1.1(p.49) ・高橋『経済学とファイナンスのための数学』(p.16); ・松坂『解析入門4』15.1-C (p. 6) |
||
|
(一般的な定義) n次単位行列とは、 すべての対角成分が「実数体Rにおける乗法の単位元『1』」であり、 なおかつ、 すべての非対角成分が「実数体Rにおける加法の単位元『0』」である、 n次正方行列のことをいう。 (クロネッカーのδをもちいた定義) n次単位行列とは、すべての( i, j )成分がδijであるn次正方行列のこと。 (具体的には)  (記号) n次単位行列は、In, En 、あるいは略して、I , E と表す。 したがって、 上記定義を記号で表すと、I=(δi j) となる。 (性質) 任意の(m,n)型実行列Aにたいして、 Im A= A A In= A が成り立つ。(∵行列の積の定義にもどって考えればわかる) |
||
|
→ [トピック一覧:実数体上の正方行列に関する様々な定義]→ 線形代数目次・総目次 |
|
定義:直交行列 orthogonal matrix |
||
|
|
|
[ 文献]・永田『理系のための線形代数の基礎』1.8(p.43); ・佐武『線形代数学』Ⅲ§7(p.123); ・佐和『回帰分析』2.2.5(p.29); ・斎藤『線形代数入門』2章§6(p.64) ・戸田山田『計量経済学の基礎:統計的手法の理論とプログラミング』2.8.2(p.112) ・松坂『解析入門4』18.2-A (p.100); ・杉浦『解析入門』Ⅱ§8(p.154) ※ 実行列はRnからRmへの線型写像 実ベクトル空間から実ベクトル空間への線形写像 を表す(→定理/定理)。 だから、実行列のタイプが論じられる際には、 それに対応する線形写像のタイプに思いをめぐらせるのが、肝要。 この「直交行列」というタイプの実行列は、 Rn上の直交変換 というタイプの一次変換を表す。 |
|
定義 |
「 n次正方行列Aが直交行列である」とは、その転置行列とそれ自身との行列積 tA A , A tAが、単位行列と等しい tA A = A tA = In ことをいう。 |
|
|
性質 |
1. 直交行列は、正則行列であって、その逆行列は、その転置行列に等しい。※なぜ?→正則行列/逆行列の定義と、直交行列の定義から。 2. 「直交行列の行列式」は、±1。 3. 実n次元数ベクトルとしての「直交行列の各列」は、 n次元ユークリッド空間Rnの正規直交系をなす。 すなわち、 直交行列Aの各列a1, a2,…, anに対して、 任意のi,j=1,2,…,nについて、ai・aj =δij (δはクロネッカーのデルタを表す。・は自然な内積を表す。) ※なぜ? (step1) n次正方行列Aの第1列を、実n次元縦ベクトルa1 n次正方行列Aの第2列を、実n次元縦ベクトルa2 : : n次正方行列Aの第n列を、実n次元縦ベクトルan とおく。 |
|
|
(step2) ・step1の設定にしたがうと、 tAの第1行は、ta1 tAの第2行は、ta2 : : tAの第n行は、tan となる。 ・行列積の定義から、 行列積tA Aの i行j列成分は、 「tAの第i行」taiと「Aの第j列」ajとの行列積 tai aj となる。 ・「n次元ユークリッド空間Rnの自然な内積」の定義より、 「tAの第i行」taiと「Aの第j列」ajとの行列積 tai aj と、 ai ,ajの自然な内積aI・aj とは等しくなる。 したがって、 行列積tA Aの i行j列成分は、 ai・aj となる。 (step3) ・「 n次正方行列Aが直交行列である」とは、 tA A = In と定義された。 ・単位行列の定義により、 Inの i行j列成分は、δij である。 ・したがって、 「 n次正方行列Aが直交行列である」とは、 「tA Aの i行j列成分は、δijである」ということに他ならない。 (step4) step2とstep3の結果より、 「 n次正方行列Aが直交行列である」とは、 「tA Aの i行j列成分ai・aj が、δijである」ということに他ならない。 [佐武p.133; 斉藤2章§6[6.4]' (p.65)証明は[6.4]を参考に] |
[amazon:tate:jp:big] |
|
|
4. ・「 n次正方行列Aが直交行列である」 ・「 n次正方行列Aの各列a1, a2,…, anは、 n次元ユークリッド空間Rnの正規直交基底をなす」 [松坂『解析入門4』18.2-A (p.100);杉浦『解析入門』Ⅱ§8(p.154)] ※なぜ? ・「 n次正方行列Aが直交行列である」 ⇒「 n次正方行列Aが正則行列である」 ⇒「 n次正方行列Aの各列a1, a2,…, anは、Rnの基底をなす」(∵) ・「 n次正方行列Aの各列a1, a2,…, anは、 n次元ユークリッド空間Rnの正規直交基底をなす」 ⇒ |
※ 関連事項:基底変換行列 |
|
|
→ [トピック一覧:実数体上の正方行列に関する様々な定義]→線形代数目次・総目次 |
|
定義:ベキ等行列・冪等行列 idempotent matrix |
||
|
|
|
[ 文献]・佐武『線形代数学』Ⅲ-研究課題1.冪等行列射影子(p.125); ・佐和『回帰分析』2.3.2(p.32); ・グリーン『計量経済分析』定義2.1(p.21) ・岩田『経済分析のための統計的方法』定理12.25;系12.1(p.309) |
|
定義 |
n次正方行列Aがn次ベキ等行列であるとは、 それ自身との行列積AAが、もとの行列Aと等しい A2=A ことをいう。 |
|
|
性質 |
・ n次正方行列Aが、ベキ等行列であり、かつ、対称行列であるならば、その転置行列とそれ自身との行列積 tA Aは、Aに等しい。 tA A =A |
|
|
・べき等行列の階数は、そのトレースに等しい。 |
[ 文献]・岩田『経済分析のための統計的方法』定理12.25;系12.1(p.309) |
|
|
例 |
射影行列 | |
|
→ [トピック一覧:実数体上の正方行列に関する様々な定義]→ 線形代数目次・総目次 |
(reference)
佐和隆光『
回帰分析』 朝倉書店、1979年、2.ベクトルと行列。→
[トピック一覧:実数体上の正方行列に関する様々な定義]→
線形代数目次・総目次