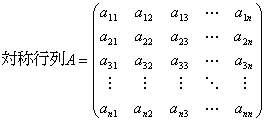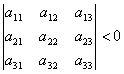定理:正値定符号行列になるための必要十分条件~主小行列式に関連して
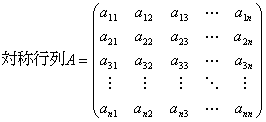
に対して、
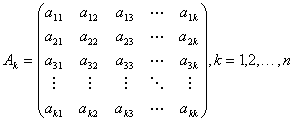
をとる。
※具体例:2変数の二次形式のケース
[文献-線型代数]
・佐武『線型代数学』Ⅳ§4 定理6(p.163) 主小行列式:対角線上にある小行列式
・木村『線形代数:数理科学の基礎』定理2.1(p.43)。
・斎藤『線形代数入門』156.
・Chiang322-326.
[文献-解析]
・杉浦『解析入門1』Ⅱ§8定理8.3(p.156):主小行列式。左上からk行k列をとった行列(1≦k≦n)=右下から(n-k)行(n-k)列除去した行列
[文献-数理統計]
・久米『数理統計学』1.33(p.32);
つまり、行列Ak (k=1,2,…n)は、
・行列Aから、同じ番号の行・列を、後から(n-1)個潰してできた主小行列:a11 、
・行列Aから、同じ番号の行・列を、後から(n-2)個潰してできた主小行列:
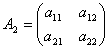
・行列Aから、同じ番号の行・列を、後から(n-3)個潰してできた主小行列:
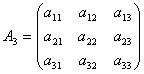
・
・
・
・行列A自体
を表している。
対称行列Aが正値定符号行列(二次形式A[x]が正値定符号)
⇔k=1,2,…nに対して、行列式det Ak>0
※
(例)
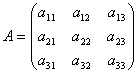
が正値定符号行列ならば、
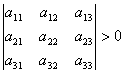
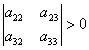
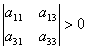
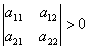
a33>0、a22、>0、a11>0
(証明)