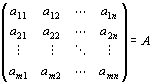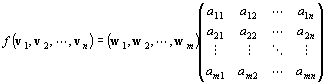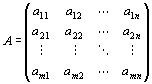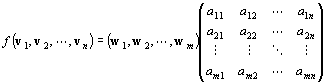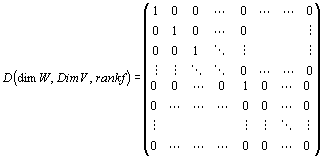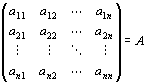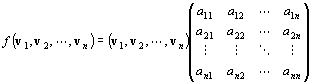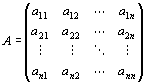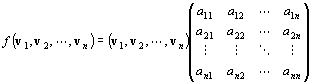一般のベクトル空間から一般のベクトル空間への一次写像の行列表示 : トピック一覧
・一次写像の行列表示/一次写像の階数と一次写像の行列表示の標準形/一次変換の行列表示/一次写像の合成写像の行列表示/同型写像の逆写像の行列表示
* 関連ページ:数ベクトル空間から数ベク
トル空間への一次写像と行列、基底の変換と一次写像と行列、一次写像の階数と行列の階数の関係
* 一般のベクトル空間を実ベクトル空間としたときの具体例:実
ベクトル空間から実ベクトル空間への一次写像の行列表示
定理:一次写像・線形写像の行列表示・行列表現
[永田『理系のための線形代数の基礎』定理1.4.1(p.28);志賀『線形代数30講』17講(p.109);
ホフマン・クンツェ『線形代数学I』3.4行列による一次変換の表現(p.89);
藤原『線形代数』4.3(p.102);神谷浦井『経済学のための数学入門』§5.2.1線形写像の行列表現(p.165)。;
酒井『環と体の理論』1.6ベクトル空間(p.23);]
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上の有限次元ベクトル空間。ただし、n次元。
{ v1, v2, …, vn }:Vの基底をなす、Vに属すベクトルの集合
W :K上の有限次元ベクトル空間。ただし、 m次元。
{ w1, w2, …, wm }:Wの基底をなす、Wに属すベクトルの集合
※体K上の有限次元ベクトル空間を実ベクトル空間としたときの具体例については、
実ベクトル空間から実ベクトル空間への一次写像の行列表示
を参照。
【本題】
1.
Vの基底{ v1, v2, …, vn },Wの基底{ w1, w2, …, wm }と、一次写像f:V→Wにたいして、
f (v1)=a11w1+a21w2+…+am1wm
f (v2)=a12w1+a22w2+…+am2wm
: :
f (vn)=a1nw1+a2nw2+…+amnwm
を満たす「体K上の(m,n)型行列」
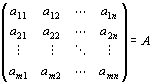
が一意的に存在する。
※
| f (v1)=a11w1+a21w2+…+am1wm
| f (v2)=a12w1+a22w2+…+am2wm
| : :
| f (vn)=a1nw1+a2nw2+…+amnwm
を、行列の乗法風に、
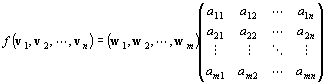
と書く、簡便法が、頻繁に用いられる。
この簡便法を用いると、上記の命題は、次のように、簡潔に表せる。
| Vの基底{ v1, v2, …, vn },Wの基底{ w1, w2, …, wm }と、一次写像f:V→Wにたいして、
| f (v1, v2, …, vn)=(w1, w2, …, wm )A
| を満たす「体K上の(m,n)型行列」Aが一意的に存在する
※なぜ?→証明
2.
Vの基底{ v1, v2, …, vn },Wの基底{ w1, w2, …, wm }と、
「体K上の(m,n)型行列」
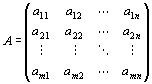
にたいして、
f (v1)=a11w1+a21w2+…+am1wm
f (v2)=a12w1+a22w2+…+am2wm
: :
f (vn)=a1nw1+a2nw2+…+amnwm
を満たす一次写像f:V→Wがきまる。
※
| f (v1)=a11w1+a21w2+…+am1wm
| f (v2)=a12w1+a22w2+…+am2wm
| : :
| f (vn)=a1nw1+a2nw2+…+amnwm
を、行列の乗法風に、
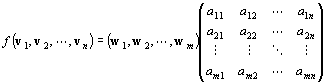
と書く、簡便法が、頻繁に用いられる。(数ベクトル空間のケースだと、便利さが引き立つらしい)
この簡便法を用いると、上記の命題は、次のように、簡潔に表せる。
| Vの基底{ v1, v2, …, vn },Wの基底{ w1, w2, …, wm }と、
| 「体K上の(m,n)型行列」Aにたいして、
| f (v1, v2, …, vn)=(w1, w2, …, wm )A
| を満たす一次写像f:V→Wがきまる。
※なぜ?→証明
3.
上記の「体K上の(m,n)型行列」Aを、
基底{ v1, v2, …, vn }, { w1, w2, …, wm }に関する1次写像fの行列表示、
基底{ v1, v2, …, vn }, { w1, w2, …, wm }を定めたとき1次写像fに対応する行列
と呼ぶ。
※関連:数ベクトル空間から数ベクトル空間への一次写像と行列
定理:一次写像の階数と、一次写像の行列表示の標準形
[永田『理系のための線形代数の基礎』定理1.6.4(p.37);斎藤『線形代数入門』4章§5[5.1](p.116);砂田『行列と行列式』§5.5-d(p.194);佐武『線形代数学』Ⅲ§7問2(p.122)]
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上の有限次元ベクトル空間。
W :K上の有限次元ベクトル空間。
「f :V→W」:一次写像
rank f :一次写像f の階数
※具体例:体K上の有限次元ベクトル空間V,Wを実ベクトル空間としたケース
【本題】
1. 一次写像f :V→W には、
f (v1)=w1, f (v2)=w2, …, f (vrankf )=wrankf , f (vrankf+1)=0 , f (vrankf+2)=0 ,…, f (vdimV)=0
を満たす
Vの基底{v1,v2,…,vdimV }、Wの基底{w1,w2,…,wdimW }(これはImagefの基底を拡大して得たWの基底)
が存在する。
※なぜ?→証明
2. したがって、1.で存在が示された、Vの基底{v1,v2,…,vdimV }、Wの基底{w1, w2, …, wdimW}をとると、
これらの基底に関する一次写像fの行列表示は、
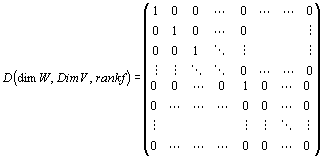
となる。
これは、
体K上の(dimW, dimV)型行列であって、
(1,1)成分, (2,2)成分, …, (rank f,rank f)成分という(rank f )個の成分が1
それ以外の成分はすべて0
となる行列である。
※ここで、少なくとも上記の基底を定めたとき一次写像fに対応する行列D(dimW, dimV,rank f)の階数は、
一次写像fの階数(rank f )と等しいことが確認できる。
では、他の基底を定めたときに一次写像fに対応する行列の階数も、
一次写像fの階数に等しいといえるのだろうか。
⇒一次写像の階数と行列の階数の関係
定理:一次変換の行列表示・行列表現
[永田『理系のための線形代数の基礎』定理1.4.1(pp.28-9);
ホフマン・クンツェ『線形代数学I』3.4行列による一次変換の表現(pp.90-91);
神谷浦井『経済学のための数学入門』§5.2.1線形写像の行列表現(p.165)。;]
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上の有限次元ベクトル空間。ただし、 n次元。
{ v1, v2, …, vn }:Vの基底をなす、Vに属すベクトルの集合
※具体例:体K上の有限次元ベクトル空間Vを実ベクトル空間としたケース
【本題】
1.
Vの基底{ v1, v2, …, vn }と、一次変換f:V→Vにたいして、
f (v1)=a11v1+a21v2+…+an1vn
f (v2)=a12v1+a22v2+…+an2vn
: :
f (vn)=a1nv1+a2nv2+…+annvn
を満たす「体K上のn次正方行列」
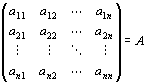
が一意的に存在する。
※
| f (v1)=a11v1+a21v2+…+an1vn
| f (v2)=a12v1+a22v2+…+an2vn
| : :
| f (vn)=a1nv1+a2nv2+…+annvn
を、行列の乗法風に、
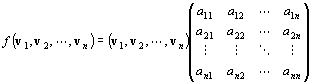
と書く、簡便法が、頻繁に用いられる。(数ベクトル空間のケースだと、便利さが引き立つらしい)
この簡便法を用いると、上記の命題は、次のように、簡潔に表せる。
| Vの基底{ v1, v2, …, vn }と、一次変換f:V→Vにたいして、
| f (v1, v2, …, vn)=(v1, v2, …, vn)A
| を満たす「体K上のn次正方行列」Aが一意的に存在する
※なぜ?→証明
2.
Vの基底{ v1, v2, …, vn }と、
「体K上のn次正方行列」
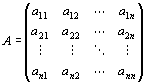
にたいして、
f (v1)=a11v1+a21v2+…+an1vn
f (v2)=a12v1+a22v2+…+an2vn
: :
f (vn)=a1nv1+a2nv2+…+annvn
を満たす一次変換f : V→Vがきまる。
※
| f (v1)=a11v1+a21v2+…+an1vn
| f (v2)=a12v1+a22v2+…+an2vn
| : :
| f (vn)=a1nv1+a2nv2+…+annvn
を、行列の乗法風に、
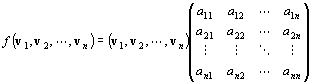
と書く、簡便法が、頻繁に用いられる。(数ベクトル空間のケースだと、便利さが引き立つらしい)
この簡便法を用いると、上記の命題は、次のように、簡潔に表せる。
| Vの基底{ v1, v2, …, vn }と、「体K上のn次正方行列」Aにたいして、
| f (v1, v2, …, vn)=(v1, v2, …, vn)A
| を満たす一次変換f : V→Vがきまる。
※なぜ?→証明
3.
上記の「体K上のn次正方行列」Aを、
基底{ v1, v2, …, vn }に関する一次変換fの行列表示、
基底{ v1, v2, …, vn }を定めたとき一次変換fに対応する行列
と呼ぶ。
※具体例:高校で習う1次変換→神谷浦井『経済学のための数学入門』§5.2.1例5.2.1(p.165)
定理:1次写像の合成写像の行列表示・行列表現
[永田『理系のための線形代数の基礎』定理1.4.2(p.29);神谷浦井『経済学のための数学入門』§5.2.2(p.169) ]
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
U :K上の有限次元ベクトル空間。ただし、 n次元。
{ u1, u2, …, un }:Uの基底をなす、Uに属すベクトルの集合
V :K上の有限次元ベクトル空間。ただし、 m次元。
{ v1, v2, …, vm }:Vの基底をなす、Vに属すベクトルの集合
W :K上の有限次元ベクトル空間。ただし、 l次元。
{ w1, w2, …, wl }:Wの基底をなす、Wに属すベクトルの集合
「f : U→V」:UからVへの一次写像
「g : V→W」:VからWへの一次写像
g〇f:一次写像fとgとの合成写像
※具体例:体K上の有限次元ベクトル空間U,V,Wを実ベクトル空間としたケース
【本題】
Uの基底{ u1, u2, …, un }, Vの基底{ v1, v2, …, vm }を定めたとき1次写像f:U→Vに対応する(m,n)型行列を、Afとおく。
Vの基底{ v1, v2, …, vm }, Wの基底{ w1, w2, …, wl }を定めたとき1次写像g:V→Wに対応する(l,m)型行列を、Agとおく。
すると、
Uの基底{ u1, u2, …, un }, Vの基底{ v1, v2, …, vm }, Wの基底{ w1, w2, …, wl }を定めたとき合成写像g〇fに対応する行列は、行列積(AgAf)で表される。
つまり、Ag〇f=(AgAf)
定理:1次写像の合成写像の結合律の行列表示・行列表現
[神谷浦井『経済学のための数学入門』§5.2.2(p.170) ]
【舞台設定】
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
U :K上の有限次元ベクトル空間。ただし、 n次元。
{ u1, u2, …, un }:Uの基底をなす、Uに属すベクトルの集合
V :K上の有限次元ベクトル空間。ただし、 m次元。
{ v1, v2, …, vm }:Vの基底をなす、Vに属すベクトルの集合
W :K上の有限次元ベクトル空間。ただし、 l次元。
{ w1, w2, …, wl }:Wの基底をなす、Wに属すベクトルの集合
「f : U→V」:UからVへの一次写像
「g : V→W」:VからWへの一次写像
g〇f:一次写像fとgとの合成写像
【本題】
定理:同型写像の逆写像の行列表示・行列表現
[永田『理系のための線形代数の基礎』系1.4.3(pp.29-30); ]
(舞台設定)
K:体 (例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
V :K上の有限次元ベクトル空間。ただし、 n次元。
{ v1, v2, …, vn }:Vの基底をなす、Vに属すベクトルの集合
W :K上の有限次元ベクトル空間。ただし、 m次元。
{ w1, w2, …, wm }:Wの基底をなす、Wに属すベクトルの集合
「f : V→W」:VからWへの一次写像
Af: Vの基底{ v1, v2, …, vn }, Wの基底{ w1, w2, …, wm }を定めたとき1次写像fに対応する行列
※具体例:体K上の有限次元ベクトル空間V,Wを実ベクトル空間としたケース
【本題】
一次写像f : V→Wが同型写像であるならば、
Vの基底{ v1, v2, …, vn }, Wの基底{ w1, w2, …, wm }を定めたとき1次写像fに対応する行列Afは正則行列であり、
Vの基底{ v1, v2, …, vn }, Wの基底{ w1, w2, …, wm }を定めたとき、fの逆写像f-1:W→Vに対応する行列は、
「Afの逆行列」Af-1 で表される。
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、項目83行列L線形写像(p.222)
線形代数のテキスト
志賀浩二『数学30講シリーズ:線形代数30講』朝倉書店、1988年、17講線形写像(pp.107-112)。
ホフマン・クンツェ『線形代数学I』培風館、1976年、3.4行列による一次変換の表現(p.89)。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.4行列と一次写像(pp.23-31)。
藤原毅夫『理工系の基礎数学2:線形代数』岩波書店、1996年、4.3線形写像の階数と行列の階数(p.102)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第2章§3行列と線形写像(p.44):実線形空間・複素線形空間のみ;。
以下未確認
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅲベクトル空間§6ベクトル空間の公理化(p.115)。線形従属・独立については、数ベクトルに限定?
代数学のテキスト
酒井文雄『共立講座21世紀の数学8:環と体の理論』共立出版、1997年、1.6ベクトル空間(p.22)。:数ページしか触れていないが、逆に、一般の線形空間の理論の骨組みだけを浮かびあがってくるので、何が重要事項なのかを見極める上で便利。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§5.2.1線形写像の行列表現(p.165)。