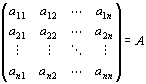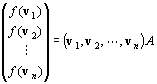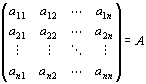→戻る

証明：一次変換の行列表示･行列表現　　
　[永田『理系のための線形代数の基礎』定理1.4.1(pp.28-9);　
　　ホフマン・クンツェ『線形代数学I』3.4行列による一次変換の表現(pp.90-91);
　　神谷浦井『経済学のための数学入門』§5.2.1線形写像の行列表現(p.165)。;]
(舞台設定)
K：体　（例：有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C）　
V ：K上の有限次元ベクトル空間。ただし、 n次元。　
{ v₁, v₂, …, v_n }：Vの基底をなす、Vに属すベクトルの集合　　　
(定理の確認)
Vの基底{ v₁, v₂, …, v_n }と、一次変換f:V→Vにたいして、　
　　 f (v₁)=a₁₁v₁+a₂₁v₂+…+a_n1v_n 　　
　　 f (v₂)=a₁₂v₁+a₂₂v₂+…+a_n2v_n 　　
　　　：　　　　　：　
　　 f (v_n)=a_1nv₁+a_2nv₂+…+a_nnv_n 　　
を満たす「体K上のn次正方行列」
　　　　　
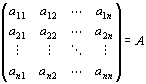
が一意的に存在する。　
　※ f (v₁), f (v₂), …, f (v_n) を縦に並べた(n,1)型行列、
　　Vの基底をなすベクトルv₁, v₂, …, v_n を横に並べた(1,n)型行列を用いると、
　　上記は、行列の乗法を使って、次のように、簡潔に表せる。　　　
　　　　　　　　
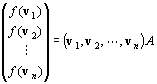
　　　　　　　を満たす「体K上のn次正方行列」Aが一意的に存在する　

（証明）　　
v₁, v₂, …, v_n ∈Vであるとされていた。
fは、VからVへの一次変換とされていた。
したがって、fによるv₁, v₂, …, v_nの像は、Vに属す。
　　　つまり、　 f (v₁), f (v₂), …, f (v_n)∈V。　…(1)　
{ v₁, v₂, …, v_n }はVの基底であるとされた。　　
よって、
Vに属す任意のベクトルを、{ v₁, v₂, …, v_n }の一次結合として一意的に表せる。（∵）　　
だから、(1)により、
　 f (v₁), f (v₂), …, f (v_n)も、それぞれ、{ v₁, v₂, …, v_n }の一次結合として一意的に表せることになる。
これは、すなわち、
　　 f (v₁)=a₁₁v₁+a₂₁v₂+…+a_n1v_n 　　
　　 f (v₂)=a₁₂v₁+a₂₂v₂+…+a_n2v_n 　　
　　　：　　　　　：　
　　 f (v_n)=a_1nv₁+a_2nv₂+…+a_nnv_n 　　
を満たす「体K上のn次正方行列」
　　　　　　　　　
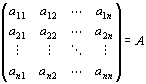
が一意的に存在するということにほかならない。