数ベクトル空間から数ベクトル空間への一次写像と行列 : トピック一覧
・定理:行列と一次写像/一次写像の行列と単位ベクトルのうつしかたの関連/一次写像の合成写像と行列
※関連ページ
・一次写像と行列の関係について:一般のベクトル空間の一次写像と行列,基底の変換と一次写像と行列
・一次写像について:一次写像-定義,一次写像と線形独立,同型写像,同型写像と線形独立
※具体例:実n次元数ベクトル空間から実n次元数ベクトル空間への一次写像と行列
定理:体K上の行列との乗法は、数ベクトル空間から数ベクトル空間への一次写像。
[永田『理系のための線形代数の基礎』(p.26-7);斎藤『線形代数入門』2章§3(pp.44-5);
佐武『線形代数学』Ⅰ§4(pp.17-19);志賀『線形代数30講』7講(pp.42-5)10講(p.63);
ホフマン・クンツェ『線形代数学I』3.4例13(p.91);;]
(舞台設定)
K:体(例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
A:体K上の(m,n)型行列
Kn:体K上のn次元数ベクトル空間。
すなわち、Kn=K×K×…×K={ ( v1, v2, …, vn )|v1∈Kかつv2∈Kかつ…かつvn∈K }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Knに属すすべての n次元数ベクトルは、 n次元縦ベクトルの形式で表されているものとする。
v:体Kからつくった n次元縦ベクトル。
Km:体K上のm次元数ベクトル空間。
すなわち、Km=K×K×…×K={ ( v1, v2, …, vm )|v1∈Kかつv2∈Kかつ…かつvm∈K }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Kmに属すすべての m次元数ベクトルは、 m次元縦ベクトルの形式で表されているものとする。
※体Kとして実数をすべて集めた集合Rを考えるケースについては、
実行列との乗法は、実n次元数ベクトル空間から実n次元数ベクトル空間への一次写像
を参照。
(本題)
1.
「体K上のn次元数ベクトル空間」Knから
「体K上のm次元数ベクトル空間」Kmへの
任意の一次写像f:Kn→Kmにたいして、
(∀v∈Kn) ( f (v)=(Av) )
を満たす「体K上の(m,n)型行列」Aが一意的に存在する。
※なぜ?→証明
2.
「体K上の(m,n)型行列」Aを用いて、
「体K上のn次元数ベクトル空間」Knから、「体K上のm次元数ベクトル空間」Kmへの写像f:Kn→Kmを、
次式で定義する。
任意の n次元縦ベクトルv∈Knにたいして、f (v)=(Av)
つまり、
Knの元である n次元数ベクトルvを、Kmの元である m次元数ベクトル(Av)にうつす写像を、
写像f:Kn→Km として定義する
*Aは「体K上の(m,n)型行列」、vは n次元縦ベクトル(つまり、(n,1)型行列)だから、
行列積の定義により、(Av)は、 m次元縦ベクトル(つまり、(m,1)型行列)となる。
すると、
任意の「体K上の(m,n)型行列」Aに対して、
(∀v∈Kn) ( f (v)=(Av) )で定義した写像f:Kn→Km は、一次写像となる。
※なぜ?→証明
3.
上記の「体K上の(m,n)型行列」Aを、
一次写像fに対応する行列、一次写像fの行列などと呼ぶ。
上記の一次写像fを、Aによって定義される一次写像などと呼ぶ。
定理:行列によって定義される一次写像は、単位ベクトルをどのように写すか
[永田『理系のための線形代数の基礎』1.4行列と一次写像:注意1(p.29);]
(舞台設定)
K:体(例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
A:体K上の(m,n)型行列
Kn:体K上のn次元数ベクトル空間。
すなわち、Kn=K×K×…×K={ ( v1, v2, …, vn )|v1∈Kかつv2∈Kかつ…かつvn∈K }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Knに属すすべての n次元数ベクトルは、 n次元縦ベクトルの形式で表されているものとする。
v:体Kからつくった n次元縦ベクトル。
Km:体K上のm次元数ベクトル空間。
すなわち、Km=K×K×…×K={ ( v1, v2, …, vm )|v1∈Kかつv2∈Kかつ…かつvm∈K }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Kmに属すすべての m次元数ベクトルは、 m次元縦ベクトルの形式で表されているものとする。
(本題)
「体K上の(m,n)型行列」
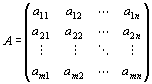
によって定義された一次写像を、f:Kn→Kmで表すと、
Knの単位ベクトルe1, e2,…, emのfによる像f ( e1 ) , f ( e2 ) , …, f ( en ) ∈Km は、
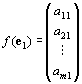
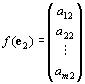
:
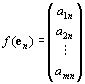
となる。
これは、単位ベクトルの定義と、行列積の定義にしたがって計算すれば、すぐわかる。
※具体例:体Kとして実数体Rを使うケース
定理:体K上の行列との乗法による一次写像の合成写像
[永田『理系のための線形代数の基礎』(p.26-7);斎藤『線形代数入門』2章§3(p.45);
佐武『線形代数学』Ⅰ§4(p.20)]
(舞台設定)
K:体(例:有理数をすべてあつめた集合Q、実数をすべて集めた集合R、複素数をすべてあつめた集合C)
A:体K上の(m,n)型行列
B:体K上の(l,m)型行列
v:体Kからつくった n次元縦ベクトル。
Kn:体K上のn次元数ベクトル空間。
すなわち、Kn=K×K×…×K={ ( v1, v2, …, vn )|v1∈Kかつv2∈Kかつ…かつvn∈K }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Knに属すすべての n次元数ベクトルは、 n次元縦ベクトルの形式で表されているものとする。
Km:体K上のm次元数ベクトル空間。
すなわち、Km=K×K×…×K={ ( v1, v2, …, vm )|v1∈Kかつv2∈Kかつ…かつvm∈K }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Kmに属すすべての m次元数ベクトルは、 m次元縦ベクトルの形式で表されているものとする。
Kl:体K上のl次元数ベクトル空間。
すなわち、Kl=K×K×…×K={ ( v1, v2, …, vl )|v1∈Kかつv2∈Kかつ…かつvl∈K }に、
ベクトルの加法とスカラー乗法を定義したもの。
ただし、Klに属すすべての l次元数ベクトルは、 l次元縦ベクトルの形式で表されているものとする。
「A:Kn→Km」:「体K上の(m,n)型行列A」と「体Kからつくった n次元縦ベクトル」との乗法による
体K上のn次元数ベクトル空間Knから、体K上のm次元数ベクトル空間Kmへの
一次写像
「B:Km→Kl」:「体K上の(l,m)型行列B」と「体Kからつくった m次元縦ベクトル」との乗法による
体K上のm次元数ベクトル空間Kmから、体K上のl次元数ベクトル空間Klへの
一次写像
(本題)
一次写像A:Kn→Km と、B:Km→Kl の合成写像B〇Aは、
行列積BA[(l,n)型行列]と「体Kからつくった n次元縦ベクトル」との乗法で表せる。
※具体例:体Kとして実数体Rを使うケース
(解説)
なぜなら、
合成写像B〇Aとは、
n次元縦ベクトル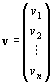 ∈Knに対して、
∈Knに対して、
B(Av)
とすること。
ところが、結合則より、
B(Av)=(BA)v
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、項目83行列L線形写像(p.222)
線形代数のテキスト
志賀浩二『数学30講シリーズ:線形代数30講』朝倉書店、1988年、7講線形写像と行列(pp.42-7)、10講R3上の線形写像(pp.62-7)、17講線形写像(pp.107-112)。
ホフマン・クンツェ『線形代数学I』培風館、1976年、3.4行列による一次変換の表現(p.89)。
永田雅宜『理系のための線形代数の基礎』紀伊国屋書店、1986年、1.4行列と一次写像(pp.23-31)。
藤原毅夫『理工系の基礎数学2:線形代数』岩波書店、1996年、4.3線形写像の階数と行列の階数(p.102)。
斎藤正彦『線形代数入門』東京大学出版会、1966年、第2章§3行列と線形写像(pp.44-5):実線形空間・複素線形空間のみ;。
佐武一郎『線形代数学(第44版)』裳華房、1987年、Ⅰベクトルと行列の演算§4一次写像(pp.17-19)。
代数学のテキスト
酒井文雄『共立講座21世紀の数学8:環と体の理論』共立出版、1997年、1.6ベクトル空間(p.22)。:数ページしか触れていないが、逆に、一般の線形空間の理論の骨組みだけを浮かびあがってくるので、何が重要事項なのかを見極める上で便利。
数理経済学のテキスト
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、§5.2.1線形写像の行列表現(p.165)。
→[トピック一覧:数ベクトル空間から数ベクトル空間への一次写像と行列]
→線形代数目次・総目次
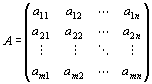
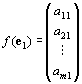
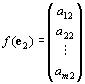
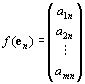
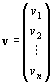 ∈Knに対して、
∈Knに対して、