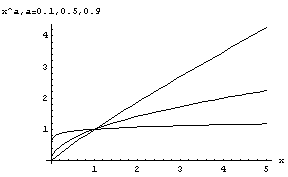
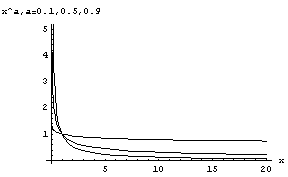
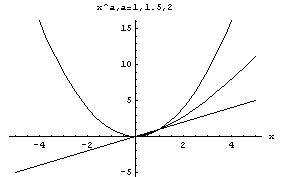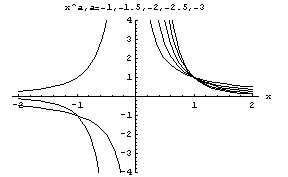実数の定数aに対して、(0,+∞)で定義された1変数関数
f (x)=xa
のことをいう。
※R=(−∞,∞)ではなく、(0,+∞)で定義するのはなぜ?
・指数aが正の整数に限定される場合は、
特に支障がないので、累乗関数 f (x)=xa は(−∞,∞)で定義できる。
・ところが、指数aを「負の整数」にまで拡張すると、
指数aが「負の整数」であって、自然数nを用いて、指数aを−nと表せるとき、
f (x)=xa=1/x n
となるから、
x=0∈Rにおいて、 f (0)=0a=1/0=φとなってしまう(∵実数体の定義)。
だから、指数aを「負の整数」にまで拡張すると、
R=(−∞,∞)で定義された対応f (x)=xa は、
関数の定義を満たさない。
指数aを「負の整数」にまで拡張した場合、
累乗関数 f (x)=xa は、
0を避けた、R−{0}=(−∞,0)∪(0, +∞) で定義せざるを得ない。
・さらに、指数aを有理数にまで拡張すると、
自然数n,整数zを用いて、a=z/nと表される場合、
| f (x)=xa= | xz | |
xが負のとき、
一定の条件下で、xz<0となって、累乗根が定義不能となる事態に陥って、
f (x)=φとなってしまって、
R=(−∞,∞)で定義された対応f (x)=xa は、
関数の定義を満たさない。
また、xが0のとき、zが負の整数なら、xz=1/0となるから、
f (x)=φとなってしまって、
R=(−∞,∞)で定義された対応f (x)=xa は、
関数の定義を満たさない。
だから、指数aを有理数にまで拡張した場合、
累乗関数 f (x)=xa は、
0と負の値を避けた、(0, +∞) で定義せざるを得ない。
※指数を《特別な実数》に限定したときの「べき関数」「累乗関数」の定義と性質は、
以下を参照。
→指数を有理数に限定した「べき関数」「累乗関数」
→指数を整数に限定した「べき関数」「累乗関数」
→指数を自然数に限定した「べき関数」「累乗関数」
[関連事項]
実数指数の累乗の定義と指数法則[文献]
・小平『解析入門I』§2.3-b) (pp.91-92);・ 松坂『解析入門1』5.2-A(p.165);
・赤攝也『実数論講義』§7.2定義7.2.2(p.210):