リーマン・スチルチェス積分 Riemann-Stieltjes integral
前:有界変動
続:スチルチェス積分の性質(1)、スチルチェス可積分条件、スチルチェス積分の性質(2)
→総目次
II.リーマンスチルチェス積分の定義
定
義:fのtに関するリーマン和、
リーマン・スチルチェス和 Riemann-Stieltjes
sum(R-S sum)
[高木『解析概論』p.131.; 杉浦『解析入門I 』351.; Lang, Real and Functional Analysis281 ;高橋『経済学とファイナンスのための数学』93-4.
; ルディン『現代解析学』6-13.]
f(x),t(x)を閉区間 I [a,b]上の関数とする。
閉区間Iの分割⊿によってできたn個の小閉区間を
I1= [a, x1] ,I2= [x1 , x2],…, In= [xn-1, b] (a=x0<x1<x2<…< xn-1< xn=b) で表し、
t(x)の小閉区間Ik両端値の差t(xk)-t(xk-1)を⊿tk で表すとする。
閉区間Iの分割⊿によってできた小閉区間Ik (k=1,2,…,n)の各々から、
代表点ζkをとり、以下のように、積:f (ζk )・⊿tk をk=1からnまで足し合せる。
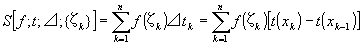
これを、
関数fの関数tに関する(分割⊿・代表点{ζk }とした際の)リーマン・スチルチェス和Riemann-Stieltjes sum
という。
※分割⊿、代表点{ζk}のとりかたは、いろいろであるから、
関数fの関数tに関するリーマン・スチルチェス和は、
分割⊿、代表点{ζk}のとりかたに応じて、値を変えうる。
関数fの関数tに関するリーマン・スチルチェス和は、分割⊿、代表点{ζk}のある種の関数となっている。
分割を細かくしていったときに、この関数が収束するかどうかという問題が、
下記の積分可能の有無に他ならない。
※ f (x)の普通のリーマン和で、k=1からnまで足し合せたのは、積:f (ζk )・⊿xk だったが、
リーマンスチルチェス和で足し合せるのは、積:f (ζk )・⊿tk
t(x)=xのときのリーマン・スチルチェス和S [ f ; t ;⊿;{ζk }]は、単なるリーマン和R [ f ;⊿;{ζk }]。
定義:リーマン・スチルチェス積分可能(S可積分)、
リーマン・スチルチェス積分
Riemann-Stieltjes integrable [ RS(g)-integrable ] ,
Riemann-Stieltjes integral with respect to g(x)
[高木『解析概論』p.131.; 杉浦『解析入門I 』351.; Lang, Real and Functional Analysis281 ;高橋『経済学とファイナンスのための数学』93-4. ; ルディン『現代解析学』6-2; 6-13;6-14.]
f(x),t(x)を閉区間I [a,b]上の関数とする。
閉区間Iの分割⊿を限りなく細かくしていくと、
分割⊿の取り方、それによってできた小区間Ik (k=1,2,…,n)の代表点ζkの取り方によらず、
fのtに関するリーマン・スチルチェス和S[ f ; t ; ⊿ ; {ζk } ] が一定値J に収束するとき、
( すなわち、分割の幅|⊿|→0で、S [ f ; t ;⊿;{ζk}] → Jとなるとき、)
fは閉区間I上でtに関し(リーマン) スチルチェス積分可能[ RS(g)-integrable ]、 (リーマン) スチルチェス可積分(S可積分)である、f∈R(t) [ルディン『現代解析学』6-2;]、などという。
※正確に書けば、
任意の(どんな)正の実数εに対して(でも)、
「 0<|⊿|<δ ならば、
分割⊿の取り方、それによってできた小区間Ik (k=1,2,…,n)の代表点ζkの取り方によらず、
|S [ f ; t ;⊿;{ζk }]-J|<ε 」
を成り立たせる、ある正の実数δが存在するとき、
関数fは閉区間I上で関数tに関しスチルチェス積分可能、S可積分であるという
となる。
※もちろん、
(i) 分割の幅|⊿|→0で、S [ f ; t ;⊿;{ζk }] → J となってスチルチェス積分可能となる場合もあれば、
(ii)分割の幅|⊿|→0で、S [ f ; t ;⊿;{ζk }] → J とならず、スチルチェス積分可能とならない場合もある。
いかなる条件下で、(ii)ではなく、(i)となるのかについては、
リーマン・スチルチェス可積分条件を見よ。
また、このとき、
値Jを「fのtに関するI上の(リーマン)スチルチェス積分Riemann-Stieltjes integral with respect to g(x)」といい、
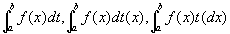
などと表す。
※ t(x)=xのときのリーマン・スチルチェス積分は、ただのリーマン積分。
※ルディン『現代解析学』におけるスチルチェス積分定義の特殊性:
普通の議論では、
分割⊿を限りなく細かくしたとき、
分割⊿の取り方に関わらず、スチルチェス和が収束することを、スチルチェス積分可能の定義とし、
そのときのスチルチェス和の収束値をスチルチェス積分の定義とするが、
ルディン『現代解析学』項目6-2.は、
「上積分=下積分」の成立(このノートのスチルチェス可積分条件の項の命題4)を「スチルチェス積分可能」の定義とし、
このときの上積分S=下積分sを「スチルチェス積分」の定義としている。
したがって、このノートでは、ルディン『現代解析学』のなかの「スチルチェス積分可能」は、「上積分S=下積分sの成立が満たされること」に、「スチルチェス積分」は、「上積分S=下積分sという値」と、置き変えて理解することにする。
※ルディン『現代解析学』における特殊な「スチルチェス積分」定義と、普通のスチルチェス積分定義の関係:
ルディン『現代解析学』は、普通のスチルチェス積分定義と、彼独特の「スチルチェス積分」(=上積分S=下積分s)とが、一致する条件を、項目6-14.において明らかにしている(証明つき)。
1.普通の意味でスチルチェス積分可能ならば、
・ルディンの意味でも「スチルチェス積分可能」(すなわち上積分S=下積分sが成立)
・普通の意味でのスチルチェス積分=ルディンの意味での「スチルチェス積分」(すなわち上積分S=下積分sの値)
だが、逆は必ずしも成りたたない。
この点は、このノートのスチルチェス可積分条件の項で、
命題1が成り立てば命題4も成り立つが、逆は必ずしも成り立たず、
命題4は、命題1の必要条件だが、十分条件ではないと、述べたことと一致する。
2.被積分関数f(x)が連続であるならば、
普通の意味でのスチルチェス積分=ルディンの意味での「スチルチェス積分」(すなわち上積分S=下積分sの値)
3.被積分関数f(x)が、ルディンの意味で「スチルチェス積分可能」(すなわち上積分S=下積分sが成立)、
かつ、
t (x) が積分区間[a,b]で連続であるならば、
普通の意味でのスチルチェス積分=ルディンの意味での「スチルチェス積分」(すなわち上積分S=下積分sの値)
この点は、杉浦『解析入門I』355-6も、
「(t(x)が閉区間[a,b]上で単調増加であるのみならず) t(x)の連続性を仮定しなければ、
上積分S=下積分sが、(普通の意味での)スチルチェス積分のための十分条件にならない(必要条件にはなる)」
と示唆している(証明なし)。
( reference )
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.93-99;104-106.
高木貞治『解析概論:改訂第3版』岩波書店、1983年、pp. 129-132;443-445.
杉浦光夫『解析入門I』東京大学出版会、1980年、p.345;pp.349-361.
Walter Rudin,Principles of Mathematical Analysis,Mcgraw-Hill,1953-1976.
=ウォ-ルタ-・ルディン『現代解析学』共立出版、1971年、第6章。
Lang,Serge.Undergraduate Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1983,pp.224-5:Exercisesとして。
Lang,Serge.Real and Functional Analysis(Graduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1993,pp.278-287.
Ross,Kenneth A.Elementary Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1980,pp.203-221.