べき関数(累乗関数)の性質〜指数を自然数に限定して　：トピック一覧　　

・べき関数のグラフ/べき関数の増減/べき関数の値域/有界性/最大最小/
・べき関数の逆像/累乗根(べき根)の定義/「自然数の逆数」を指数とする累乗の定義/累乗根(べき根)の性質 
・分数を指数とする累乗の定義/m乗のn乗根の意味/「分数を指数とする累乗」「m乗のn乗根」の性質　　
・べき関数の単射/全射/全単射の判定 / べき関数の逆関数 / 　
・べき関数の極限/連続/極大極小　　
※1変数関数の具体例：y=x / y=x2/ y=x3 / y=1/x  →整数指数のべき関数/有理数指数のべき関数/実数指数のべき関数
　　　　　　　　　　 定数値関数/比例/一次関数/二次関数/三次関数→多項式関数　　
　　　　　　　　　　　指数関数/対数関数　
　　　　　　　　　　　絶対値関数/三角関数　/ガンマ関数
※1変数関数に関する諸概念の定義：1変数関数一般の定義/極限/連続性/微分/定積分/広義積分/スチルチェス積分
※関数定義関連ページ：2変数関数/n変数関数/実数値関数一般/ベクトル値関数/写像一般
※総目次

定義：べき関数（累乗関数）　〜指数を自然数に限定して

定義

 ・指数を自然数とする「冪(べき)関数」「累乗関数」とは、
　　自然数の定数nに対して、
　　　R＝(−∞,∞)もしくは「Rの部分集合」で定義された1変数関数
　 　　　y=f (x)=xn 
　　のことをいう。　　
※指数が自然数ではない「べき関数」「累乗関数」もつくれるが、
　定義域はR＝(−∞,∞）に設定できなくなる。性質もことなる。
　　　→指数が正負の整数となる「べき関数」「累乗関数」
　　　→指数が有理数となる「べき関数」「累乗関数」
　　　→指数が実数となる「べき関数」「累乗関数」

[関連事項]

　自然数指数の指数法則　




[文献−解析]
　・小平『解析入門I』§2.3-a) (p.89);「巾関数」。定義域は(0,∞)
　・ 松坂『解析入門1』3.2E-例(p.113)：n乗根関数（n乗根の定義）も。「累乗関数」。定義域は[0,∞)




グラフ
R＝(−∞,∞）で定義された、自然数を指数とする「べき関数」（累乗関数）
y=x

のグラフは、下図の通り。

べき関数のグラフ（指数を自然数に限定）

[y=xn(aは自然数)のグラフの形状]

　nがいかなる自然数であったとしても、y=xn(nは自然数)のグラフは、(1,1)を通る。
　しかし、これ以外の特徴は、nが偶数であるか、奇数であるかによって、変わってくる。
・nが偶数であるとき、y=xn(nは自然数)のグラフの形状は、
 　 ・原点(0,0)でx軸に接する
　　・下に凸な　
　　・R2上の放物線
　　であって、
　　(1,1),(0,0),(-1,+1)が、共通した通過点である。
・nが3以上の奇数であるとき、y=xn(nは自然数)のグラフは、
　　「原点(0,0)でx軸に接する下に凸なR2上の放物線の右半分」
　　と
　　「原点(0,0)でx軸に接する上に凸なR2上の放物線の左半分」
　とを、張り合わせた形状。
　　(1,1),(0,0),(-1,-1)が、共通した通過点となる。

　[0,∞)で定義された、自然数を指数とする「べき関数」 （累乗関数）
y=x

　のグラフは、下図の通り。

[0,∞)で定義されたべき関数のグラフ（指数を自然数に限定）




→[トピック一覧:べき関数]
→総目次

自然数指数の冪関数（累乗関数）の増減

→(-∞,∞)で定義された冪関数の増減　
→[0,∞)で定義された冪関数の増減　




【文献-自然数を指数とするべき関数】
　・赤攝也『実数論講義』§6.5例4(p.188):。
　・小平『解析入門I』§2.3-a) (p.89);「巾関数」

【関連事項】
　・自然数指数の「べき関数」「累乗関数」の増減の一般化：
　　→指数を正負の整数に拡張した「べき関数」「累乗関数」の増減
　　→指数を有理数に拡張した「べき関数」「累乗関数」の増減
　　→指数を実数に拡張した「べき関数」「累乗関数」の増減　







　性質

 ・R＝(−∞,∞）で定義された自然数指数の「べき関数」「累乗関数」
　 　　　y=f (x)=xn 
　は、
　・nが奇数ならば、(−∞,＋∞)で狭義単調増加関数　　 　
　・nが偶数ならば、(−∞,＋∞)で単調関数にならないが、
　　　　　　　　　　　(−∞,0]で狭義単調減少関数、
　　　　　　　　　　　[0,＋∞)で狭義単調増加関数となる。

図解



y=x のグラフ

R＝(−∞,∞）で定義された自然数指数の「べき関数」

べき関数のグラフ（指数を自然数に限定）

　性質

 ・[0,∞)で定義された自然数指数の「べき関数」「累乗関数」
　 　　　y=f (x)=xn 
　は、[0,＋∞)で狭義単調増加関数

図解
　[0,∞)で定義された、自然数を指数とする「べき関数」 （累乗関数）
y=x

　のグラフは、下図の通り。

[0,∞)で定義されたべき関数のグラフ（指数を自然数に限定）

→[トピック一覧:べき関数]
→総目次


自然数指数の冪関数（累乗関数）による値・像image　
　 ・　　

※定義の確認→1変数関数による値・像の定義　

→[トピック一覧:べき関数]
→総目次

冪関数（累乗関数）の値域
　 ・R＝(−∞,∞）で定義された自然数指数の「べき関数」「累乗関数」　
　 　y=f (x)=xn 
　の値域は、
　・nが奇数ならば、R＝(−∞,∞）　　 　
　・nが偶数ならば、[0,∞)
・[0,∞)で定義された自然数指数の「べき関数」「累乗関数」　
　 　　　y=f (x)=xn 
　の値域は、nが奇数であろうが偶数であろうが、　[0,∞) 。
 　

[図解]
y=x のグラフ

R＝(−∞,∞）で定義された自然数指数の「べき関数」

べき関数のグラフ（指数を自然数に限定）




[文献-自然数を指数とするべき関数]
　・赤攝也『実数論講義』§6.5定理6.5.5(p.193):。
　・小平『解析入門I』§2.3-a) (p.89);「巾関数」






→[トピック一覧:べき関数]
→総目次

自然数指数の冪関数（累乗関数）の最大値・最小値
　 ・R＝(−∞,∞）で定義された自然数指数の「べき関数」「累乗関数」　
　 　　　y=f (x)=xn 
　は、
　　　nが奇数ならば 最大値・最小値ともにもたない。　
　　　nが偶数ならば 最大値をもたないが、最小値は有していて、f(0)＝0が最小値。　　

自然数指数の冪関数（累乗関数）は非有界
　 ・R＝(−∞,∞）で定義された自然数指数の「べき関数」「累乗関数」　
　 　　　y=f (x)=xn 
　は、有界でない。
・細かく見ると、
　・nが奇数ならば、下に有界でなく、上にも有界でない。　　 　
　・nが偶数ならば、下に有界だが、上に有界ではないので、有界でない。


[図解]

y=x のグラフ

R＝(−∞,∞）で定義された自然数指数の「べき関数」


べき関数のグラフ（指数を自然数に限定）

→[トピック一覧:べき関数]
→総目次


自然数指数の冪関数(累乗関数)による逆像

→(-∞,∞)で定義された冪関数による逆像　　※限定した具体例→(-∞,∞)で定義されたy=x2による逆像/(-∞,∞)で定義されたy=x3による逆像 　　　
→[0,∞)で定義された冪関数による逆像→「累乗根」の定義,「1/自然数を指数とする累乗」の定義　　※限定した具体例→ √ / 3√ 　
[図解：(-∞,∞)で定義された自然数指数の冪関数による逆像]

・「R＝(−∞,∞）で定義された累乗関数」y=f (x)=xn による実数yの逆像」
　　　　f −1 (y)
　とは、
　「『fの値(像)xn』 が実数yとなる実数x」をすべてあつめた 集合のこと。
・つまり、　f −1 (y)＝{x∈R|y＝xn}

・R＝(−∞,∞）で定義された自然数指数の累乗関数」


y=f(x)=x



　　による　y= の逆像　f-1(　　) 　を図示すると…
　　　べき関数による逆像

[文献]

　・『岩波数学入門辞典』べき根(p.546)
　・吉田栗田戸田『昭和63年3/31文部省検定済　高等学校基礎解析』2章1.指数の拡張-[累乗根](p.41)。
　・KIT数学ナビゲーション　
 　　　上記2文献では、「(−∞,∞）で定義された累乗関数」y=f (x)=xn (nは自然数)による実数yの逆像をn乗根と呼び、
　　　nが奇数のとき、一つしかない「実数yのn乗根」とを√yで表し、
　　　nが偶数のとき、二つある「実数yのn乗根」の正の方を√yで表す、としている。
　　　
　・小平『解析入門I』§2.3-a) (p.89):n乗根一般。
  ・ 松坂『解析入門1』3.2E-例(p.113):n乗根一般。
　・赤攝也『実数論講義』§6.5定義6.5.3(p.197):。
　　　上記文献では、
　　　「[0,∞)で定義された累乗関数」y=f (x)=xn (nは自然数)による実数yの逆像に属す元を『正の実数』をn乗根と呼び、
　　　　√yで表す、としている。

　・斉藤正彦『数学の基礎：集合・数・位相』3章§1問題2(p.73)




[解説：逆像〜単射〜逆関数]

・左図からわかるように、
　「R＝(−∞,∞）で定義された累乗関数」y=f (x)=xn (nは自然数)　は、
　　 　nが奇数ならば、 Rの上への全単射となって、逆関数を有すが、
　　 　nが偶数ならば、単射にならないので、逆関数を有しない。

[図解:[0,∞)で定義された自然数指数の冪関数による逆像]

・「[0,∞)で定義された累乗関数」y=f (x)=xn (nは自然数)による実数yの逆像」f −1 (y)
　とは、
　　「『fの値(像)』xnが実数yとなる『定義域[0,∞)に属す実数』x」を
　　すべてあつめた集合のこと。
・つまり、f −1 (y)＝{x∈[0,∞)|y＝xn}




y=f(x)=x による
[図]
 [0,∞)で定義された自然数指数の累乗関数」

　　　　 　y= の逆像　　f-1(　　) 　を図示すると…
　　　べき関数による逆像


[累乗根の定義、1/自然数を指数とする累乗の定義]

[解説：逆像〜単射〜逆関数]

・「[0,∞)で定義された累乗関数y=f (x)=xn (nは自然数)」に関して、
　以下が成り立つ。
　　　(i)任意の非負の実数yに対して、
　　　　　yのfによる逆像 f−1(y)は、「1個の『非負の実数』のみが属す一元集合」となる。
　　　(ii)任意の負の実数yに対して、
　　　　　yのfによる逆像 f−1(y)は、空集合。

　つまり、「[0,∞)で定義された累乗関数y=f (x)=xn (nは自然数)」は、
　　　　　　つねに、単射。
　したがって、「[0,∞)で定義された累乗関数y=f (x)=xn (nは自然数)」には、
　　　　　　つねに、逆関数が存在する。

[累乗根の定義]

・「[0,∞)で定義されたy=f (x)=xn(nは自然数)」は単射だから、
　　任意の正の実数yにたいして、
　　　「正の実数yの『[0,∞)で定義されたy=f (x)=xn(nは自然数)』による逆像」f−1(y)は、
　　　　　「1個の『正の実数』のみが属す一元集合」となるが、
　　この一元集合f−1(y)　に唯一つ属す『正の実数』を、　
　　　　記号　  n
 y 
　または、　y1/n 　　　　
　　で表す。
　　※活用例：有理数指数の冪と指数法則/有理数指数の冪関数　

・「[0,∞)で定義されたy=f (x)=xn(nは自然数)」の逆関数「[0,∞)で定義された1変数関数x=f-1(y)」を、
　　　　x=f-1(y)＝  n y 
　または、　x=f-1(y)＝y1/n 　
　　で表す。

※累乗根を限定した具体例→ √ / 3√ / n√　

・「正の実数yの『[0,∞)で定義された累乗関数 y=f (x)=xn(nは自然数)』による逆像」 f−1(y) には、

　　1個の『正の実数』のみが属すが、
　この　「 f -1(y)に唯一つ属す『正の実数』」を、
 「実数yのn乗根」と呼び、
　　　　　　　記号　  n
 y 
　または、　y1/n 　　　　
　で表す。

・つまり、
　　任意の正の実数y,任意の自然数n 、[0,∞)で定義されたy=f (x)=xn　に対して、
　　　　　　　f−1(y)  ＝　  {
n
 y 
 } 　　　　　　

・要するに、　
　　自然数n、正の実数yに対して、  n
 y 
、y1/n とは、　　
　　　　　　条件「y=xn かつ　x≧0」を満たすxのこと。
　
※活用例：分数を指数とする累乗の定義/有理数指数の冪と指数法則/有理数指数の冪関数　
[2乗根の略記法]

　正の実数yに対して、 2 y
は、
y　
 と略記されるのが普通。

[1乗根の性質]

　正の実数yに対して、 1 y
＝y　となる。

　※なぜ？　
　　　左辺は「正の実数yの 『[0,∞)で定義された累乗関数 y=f (x)=x』 による逆像」f−1(y) だが、
　　　グラフを見ると、「正の実数yの『[0,∞)で定義された累乗関数 y=f (x)=x』 による逆像」f−1(y) ＝y だとわかる。

　※　 1 y
を、y1/1 と書くと、1/1＝１　だから、y1/1 ＝y1 ＝y　となって、　
　 　　　この記法も、上記の原意に立ち返った説明と整合的になる。

[1の累乗根の性質]
　
　　任意の自然数nに対して、  n
 1 
　＝ 1　　　

　※なぜ？　
　　　任意の自然数nに対して、[0,∞)で定義されたy=f (x)=xnは、1＝f(1)＝1n＝1 を満たすから、
　　　任意の自然数nに対して、「1の 『[0,∞)で定義されたy=f (x)=xn』 による逆像」f−1(1)＝1。
　

→[トピック一覧:べき関数]
→総目次

累乗根(べき根)の性質

要約
[性質0-1]

・任意の正の実数a,自然数n に対して、a＝ (
 a )
 n
・分数を指数とする累乗を用いて言い直すと、
　　　　　　任意の正の実数a,自然数n に対して、a＝(a1/n)n　　
※なぜ？→説明
　　　　　
[性質0-2]　　　　　　　　　　

・任意の正の実数a,自然数n に対して、a＝ an
・分数を指数とする累乗を用いて言い直すと、
　　　　　　任意の正の実数a,自然数n に対して、a＝(an)1/n　
※なぜ？→説明
　　　　　　
[性質1]　　　

・任意の正の実数a,b,自然数n に対して、 ab
　＝　
 a 
b 
・分数を指数とする累乗を用いて言い直すと、
　　　　　正の実数a,b,自然数n に対して、
 　　　　　　　　　　　(ab)1/n ＝ a1/n b1/n   
・つまり、「積の累乗根」と「累乗根の積」が一致するという意味で、
　　　　　積と累乗根の順序は入れ替え可能。
※なぜ？→説明

[性質2]

・正の実数a,b,自然数n に対して、 a/b
 　＝　
 a /
 b
・分数を指数とする累乗を用いて言い直すと、
　　　　　(a/b)1/n ＝ （a1/n）/（b1/n） 

[性質3]

・正の実数a,自然数n,m に対して、

 m
　＝　

　　　　 a
mn
 a
・分数を指数とする累乗を用いて言い直すと、
  　　　　（a1/n）1/m　 ＝ a1/mn  
※なぜ？→説明




[文献−解析]
　・赤攝也『実数論講義』§6.5定義6.5.3(pp.198);§7.1定理7.1.1-2;補題(pp.204-5):証明つき。
　・吉田栗田戸田『昭和63年3/31文部省検定済　高等学校基礎解析』啓林館、2章1指数の拡張(p.42);.
　・小平『解析入門I』§2.3-a) (p.89):有理数指数での表現。

【関連事項】
※1変数連続関数の定義
※1変数関数の具体例の連続性：
　　　定数値関数/y=x/比例/一次関数/反比例/二次関数/べき関数
　　　指数関数/対数関数/絶対値関数/三角関数/ガンマ



性質0-1
・任意の正の実数a,自然数n に対して、a＝ (
 a )
 n

[文献]

　・吉田栗田戸田『数学Ｉ』p.53:平方根のケースで。

※なぜ？
・累乗根の定義より、
　任意の正の実数a,自然数n に対して、 a 　とは、
　　「正の実数aの『[0,∞)で定義された累乗関数y=f (x)=xn 』による逆像」f-1(a)に唯一属す「正の実数」

　　　　　　　　平たく言うと、「a=xn かつ　x≧0」を満たす唯一の実数xのこと
　　を、そもそも表していた。
　　だから、この記号の意味に立ち返ると、
　　　　a＝ (
 a )
 n
　　は、自明だとわかる。

　※ここでやっている操作は、
　　  「正の実数aの『[0,∞)で定義された累乗関数y=f (x)=xn 』による逆像」
　　　　　　　の『[0,∞)で定義された累乗関数y=f (x)=xn 』による像　　　　　
　　　　　　　　　　f ( f-1(a))　
　　　をとることに他ならない。[→逆像の像]　
　　[→赤攝也『実数論講義』§6.5定義6.5.3(pp.198)で指摘]


 aのn乗根
　　　　　　　　　

→[累乗根の性質に戻る]

性質0-2
・任意の正の実数a,任意の自然数n に対して、a＝ an



※なぜ？

[step0:累乗関数と累乗根の性質の確認]

・任意の自然数n に対して、
　　『[0,∞)で定義された累乗関数y=f (x)=xn 』は、
　　　　　　　単射であって、[0,∞)を値域とする。…(0-1)
・任意の正の実数y,任意の自然数n に対して、
　yは「『[0,∞)で定義されたy=f (x)=xn』の値域」[0,∞)に属しているから、
　(0-1)より、
　yの『[0,∞)で定義されたy=f (x)=xn』による逆像 f-1(y)＝{x∈[0,∞)|y＝f (x)}は、
　　　　[0,∞)上に存在する1個の実数　
y
だけからなる。

　　つまり、
　　任意の正の実数y,任意の自然数n に対して、
　　　　　　　　　　 y   　∈[0,∞)であって、

　　　　　　　　　　　f−1(y)  ＝　  {
y   } 　…(0-2)　　

　・このことは、
　　　[0,∞)上に存在する1個の実数　
y
のほかに、
　　　　　　　　　　　　　f−1(y) に属す実数が、存在しない
　　　ことを意味している。　　　　　　　　　　　　　　…(0-3)　


[左記step0の図解]
 

[step1:累乗関数と累乗根の性質からanの累乗根について言えること]

・任意の正の実数a,任意の自然数n に対して、an＝aa…a>0　…(1-1)
　　　　　　∵　a>0であって、an＝aa…aだから、実数 の積の正負の性質より。
・(0-2)と、(1-1)より、
　任意の正の実数a、任意の自然数nに対して、
　「anの『[0,∞)で定義されたy=f (x)=xn』による逆像」f-1(an)＝{x∈[0,∞)|an=f (x)}
　は、[0,∞)上に存在する1個の実数　
an
だけからなる。

　　　　　つまり、　 an  　∈　[0,∞)　であって、

　　　　　　　　　　　f−1(an)  ＝　  {
an   } 　　…(1-2)　　

　・このことは、
　　　[0,∞)上に存在する1個の実数　
an
のほかに、
　　　　　　　　　　　　　f−1(an)  に属す実数が、存在しない
　　　ことを意味している。　　　　　　　　　　　　　　…(1-3)　




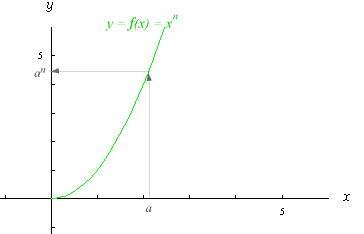
[step2]


・任意の正の実数a,任意の自然数n に対して、
　　　　　anは「正の実数aの『[0,∞)で定義された累乗関数y=f (x)=xn 』による像」
　　である。
　　つまり、an＝f ( a)　…(2-1)

・(2-1)と、
　「anの『[0,∞)で定義されたy=f (x)=xn 』による逆像」の定義
　　　　f−1(an)＝{x∈[0,∞)|an＝f ( x)} 　　
　から、
　任意の正の実数a,任意の自然数n に対して、
　　　　aは「anの『[0,∞)で定義されたy=f (x)=xn 』による逆像」f−1(an) に属す
　　　　a ∈ f−1(an)
　と言える。　…(2-2) 　　


[step3:結論]

・任意の正の実数a、自然数n に対して、
　　aは、[0,∞)上に存在して、[∵aは正の実数としたのだから]
　　　　「anの『[0,∞)で定義されたy=f (x)=xn 』による逆像」f−1(an) に属す
　　　　　　　　　　　　　　　[∵(2-2)]
・つまり、
　　任意の正の実数a、自然数n に対して、
　　　　　　　a ∈  [0,∞)　であって、　a ∈ f−1(an) 　…(3)

・ところが、(1-2)(1-3)で明らかにされたように、　　
　　　　任意の正の実数a、任意の自然数nに対して、f−1(an)＝  { an  }

　つまり、任意の正の実数a、任意の自然数nに対して、
　「anの『[0,∞)で定義されたy=f (x)=xn』による逆像」f−1(an)　に属すのは、
　　　[0,∞)上に存在する1個の実数　
an
だけであって、

　　　[0,∞)上に存在する1個の実数　
an
のほかには、
　　　「anの『[0,∞)で定義されたy=f (x)=xn』による逆像」f-1(an)に属す実数
　は存在しない。

・したがって、　(1-2)(1-3)で明らかになったこの事実と、(3)から、
　　　任意の正の実数a,任意の自然数n に対して、a＝ an
　となることがわかる。

[補足]

・任意の正の実数a,任意の自然数n に対して、
　　　　　anは「正の実数aの『[0,∞)で定義された累乗関数y=f (x)=xn 』による像」
　　である。
　　つまり、an＝f ( a)

・累乗根の定義より、
　　任意の正の実数a,自然数n に対して、 {
 an }
 　は、
　　「正の実数anの『[0,∞)で定義された累乗関数y=f (x)=xn 』による逆像」f-1(an)

・つまり、ここでやっている操作は、
　　  「正の実数aの『[0,∞)で定義された累乗関数y=f (x)=xn 』による像」
　　　　　　　　　　の『[0,∞)で定義された累乗関数y=f (x)=xn 』による逆像　
　　　　　　　　　f-1(　f ( a)　)
　　　をとることに他ならない。[→像の逆像]　
　　[→赤攝也『実数論講義』§6.5定義6.5.3(pp.198)で指摘]

・一般には、「{a}＝ f-1( f ( a) )」とはならないが、　
　『[0,∞)で定義された累乗関数y=f (x)=xn 』は、[0,∞)の上への全単射なので、
　　　　　　{a}　＝　f-1(　f (a)　)
　となる[→像の逆像の性質]。

※「{a}＝ f-1( f ( a) )」とはならない場合を確認したいならば、
　　[0,∞)で定義された累乗関数y=f (x)=xn (nは自然数)の代わりに、
　　「Rで定義された累乗関数」y=f (x)=xn(nは偶数)を使えばよい。
　　任意の正の実数a,任意の偶数n に対して、
　　　　{a, -a}＝ f-1( f ( a) )
　　となることがわかるだろう。
　　
→[累乗根の性質に戻る]





性質1

 ・任意の正の実数a,b,自然数n に対して、
　　　　 ab
 　＝　
 a 
b 
・分数を指数とする累乗を用いて言い直すと、
　正の実数a,b,自然数n に対して、
 　　　　　(ab)1/n ＝ a1/n b1/n  
・つまり、「積の累乗根」と「累乗根の積」が一致するという意味で、
　　　　　積と累乗根の順序は入れ替え可能。
　　　　　　




[文献−解析]
　・赤攝也『実数論講義』§7.1補題(i)(p.205):証明つき。
　・吉田栗田戸田『昭和63年3/31文部省検定済　高等学校基礎解析』啓林館、2章1指数の拡張(p.41):証明なし。いきなり「累乗根について次のことが成り立つ」.

　・吉田栗田戸田『高等学校　数学I』2章2実数(p.53):平方根について。証明つき.



　

※なぜ？

[step0:累乗関数と累乗根の性質の確認]


　・任意の自然数n に対して、
　　『[0,∞)で定義された累乗関数y=f (x)=xn 』は、
　　　　　　　単射であって、[0,∞)を値域とする。…(0-1)
　・任意の正の実数y,任意の自然数n に対して、
　　yは「『[0,∞)で定義されたy=f (x)=xn』の値域」[0,∞)に属しているから、
　　(0-1)より、
　　yの『[0,∞)で定義されたy=f (x)=xn』による逆像 f-1(y)は、
　　　　[0,∞)上に存在する1個の実数　
y
だけからなる。
　　　　　　　　
　　　　　つまり、　 y   　∈　[0,∞)　であって、

　　　　　　　　　　　f−1(y)  ＝　  {
y   } 　…(0-2)　　

　　・このことは、
　　　[0,∞)上に存在する1個の実数　
y
のほかに、
　　　　　　　　　　　　　f−1(y) に属す実数が、存在しない
　　　ことを意味している。　　　　　　　　　　　　　　…(0-3)　

[左記step0の図解]
 

[step1:累乗関数と累乗根の性質からabの累乗根について言えること]


　　・実数 の積の正負の性質より、
　　　　　　任意の正の実数a,bに対して、 ab>0　　　 …(1-1)　

　　・(0-2)と、(1-1)より、
　　　任意の正の実数a,b、任意の自然数nに対して、
　　　　　abの『[0,∞)で定義されたy=f (x)=xn』による逆像 f-1(ab)は、
　　　　[0,∞)上に存在する1個の実数　
ab
だけからなる。

　　　　　つまり、　 ab   　∈　[0,∞)　であって、

　　　　　　　　　　　f−1(ab)  ＝　  {
ab   } 　　…(1-2)　　

　　・このことは、
　　　[0,∞)上に存在する1個の実数　
ab
のほかに、
　　　　　　　　　　　　　f−1(ab) に属す実数が、存在しない
　　　ことを意味している。　　　　　　　　　　　　　　…(1-3)　

 [左記step1の図解]

[step2:指数法則から言えること]

　・任意の正の実数a,b,自然数n に対して、
　　　 (
 		a 
b  )
 n
 ＝( a 
  ) n
( b
) n 　　∵指数法則3　
　　　　　　　　　　　　＝ab 　　　∵累乗根の性質0-1

　・要するに、
　　　任意の正の実数a,b、自然数n に対して (
 		a 
b  )
 n
 ＝ab　…(2-1)

　・このことは、
　　　　任意の正の実数a,b、自然数n に対して、
　　
　　　　  a  
b  
の『[0,∞)で定義されたy=f (x)=xn』による像がabであること

　　　　　　　　　　 f (
 		a 
b  )
 ＝ab　…(2-2)
　　を意味する。

 [step3]

　・任意の正の実数a,b、自然数n に対して、
　　　　　　　(0-2)より、  a  　≧0、
 b  　≧0 　　…(3-1)　

　・任意の正の実数a,b、自然数n に対して、
　　　　　(3-1)と実数の積の正負の性質より、  a 
b  　≧0 　　…(3-2)　

　・このことは、
　　　　  a 
b  　が、[0,∞)上に存在するということ　…(3-3)　
　　を意味する。　　


[左記step2〜step3の図解]

[step4:結論]

・任意の正の実数a,b、自然数n に対して、
　  a  
b  
は、[0,∞)上に存在して、[∵(3-2)および(3-3)]
　　　　　　　　　「abの『[0,∞)で定義されたy=f (x)=xn 』による逆像」f−1(ab)に属す。[∵(2-2)]
・つまり、任意の正の実数a,b、自然数n に対して、
　　　　　　  a  
b  
　∈　[0,∞)　

　　　　　　  a  
b  
　∈　f−1(ab)　…(4) 

・ところが、(1-2)(1-3)で明らかにされたように、
　　　　任意の正の実数a,b、任意の自然数nに対して、　f−1(ab)  ＝　  {
ab   } 　。　　
　つまり、任意の正の実数a,b、任意の自然数nに対して、
　　　　　　　「abの『[0,∞)で定義されたy=f (x)=xn 』による逆像」f−1(ab)に属すのは、
　　　　　　　　　　　　　　　　　　[0,∞)上に存在する1個の実数　
ab
だけであって、　

　　　　　　　[0,∞)上に存在する1個の実数　
ab
のほかには、　
　　　　　　　「abの『[0,∞)で定義されたy=f (x)=xn 』による逆像」f−1(ab)に属す実数は存在しない。

・したがって、　(1-2)(1-3)で明らかになったこの事実と、(4)から、
　　　　　任意の正の実数a,b,自然数n に対して、　 ab
 　＝　
 a 
b 
　となることがわかる。

→[累乗根の性質に戻る]

性質2

 正の実数a,b,自然数n に対して、
　　　　 n
 a/b
 　＝　
 n
 a /
 n b
　　　　　(a/b)1/n ＝ （a1/n）/（b1/n）    
  

[文献]

　・赤攝也『実数論講義』§7.1補題(ii)(p.205):証明なし。
　・吉田栗田戸田『昭和63年3/31文部省検定済　高等学校基礎解析』啓林館、2章1指数の拡張(p.41):証明なし。いきなり「累乗根について次のことが成り立つ」.

性質3

 ・正の実数a,自然数n,m に対して、

 m
　＝　

　　　　 n
 a
mn
 a
・分数を指数とする累乗を用いて言い直すと、
　　　　（a1/n）1/m　 ＝ a1/mn  

[文献]

　・赤攝也『実数論講義』§7.1補題(iii)(p.205):証明つき。
　・吉田栗田戸田『昭和63年3/31文部省検定済　高等学校基礎解析』啓林館、2章1指数の拡張(p.41):証明なし。いきなり「累乗根について次のことが成り立つ」.

※なぜ？

[step0:累乗関数と累乗根の性質の確認]

　・任意の自然数n に対して、
　　『[0,∞)で定義された累乗関数y=f (x)=xn 』は、
　　　　　　　単射であって、[0,∞)を値域とする。…(0-1)
　・任意の正の実数y,任意の自然数n に対して、
　　yは「『[0,∞)で定義されたy=f (x)=xn』の値域」[0,∞)に属しているから、
　(0-1)より、
　「yの『[0,∞)で定義されたy=f (x)=xn』による逆像」 　
　　　　f-1(y)＝{x∈[0,∞)|y＝f (x)}
　　は、
　　[0,∞)上に存在する1個の実数　
y
だけからなる。

　　つまり、
　　任意の正の実数y,任意の自然数n に対して、
　　　　　　　　　　 y   　∈[0,∞)であって、

　　　　　　　　　　　f−1(y)  ＝　  {
y   } 　…(0-2)　　

　・このことは、
　　　[0,∞)上に存在する1個の実数　
y
のほかに、
　　　　　　　　　　　　　f−1(y) に属す実数が、存在しない
　　　ことを意味している。　　　　　　　　　　　　　　…(0-3)　







[step1:累乗関数と累乗根の性質からaの累乗根について言えること]

　・任意の正の実数a、任意の自然数m,nに対して、
　　　　　　　　　　mnは自然数になるから、(0-2)より、
　　「aの『[0,∞)で定義されたy=f (x)=xmn』による逆像」
　　　　　f−1(a)＝{x∈[0,∞)|a=f (x)}
　　は、
　　[0,∞)上に存在する1個の実数　 mn
 a   だけからなる。

　　　　　つまり、　 mn
 a  　∈　[0,∞)　であって、

　　　　　　　　　　　f−1(a)  ＝　  {
mn

 a   } 　　…(1-2)　　

　・このことは、
　　　[0,∞)上に存在する1個の実数　 mn
 		a
のほかに、
　　　　　　　　　　　　　f−1(a)  に属す実数が、存在しない
　　　ことを意味している。　　　　　　　　　　　　　　…(1-3)　






[step2:指数法則から言えること]

　・任意の正の実数a,自然数m,n に対して、

 ( m
) mn
 　
　　　　 n
 a



= (( m
) m
 ) n
 　∵指数法則2　
　　　　 n
 a



　　　　 = (
 n
 a
)
 n 　∵累乗根の性質0-1 　
　　　　＝a  　∵累乗根の性質0-1 　
　・要するに、
　　　任意の正の実数a,自然数m,n に対して、 ( m
) mn
  ＝ a　…(2-1)
n
 a

　・このことは、
　　任意の正の実数a、任意の自然数m,n に対して　　
　 　 m
　の『[0,∞)で定義されたy=f (x)=xmn』による像がaであること
n
 a

　　　　　　　　　　　　　  f ( m
)  ＝a　…(2-2)
n
 a
　を意味する。






[step3]

　・任意の正の実数a、任意の自然数n に対して　
　　　　　　　(0-2)より、  a  　≧0
 　　…(3-1)　
　
　・任意の正の実数a、自然数m,n に対して、
　　(0-2),(3-1)より、
　　　　 　 m
　≧0 　　　　　　…(3-2) 
a

　・このことは、
　 　 ( m
) が[0,∞)に存在するということ　…(3-3)
n
 a
　　を意味する。

[step4:結論]


・任意の正の実数a、自然数m,n に対して、
　  ( m
) は、[0,∞)に存在して、[∵(3-2)および(3-3)]　
n
 a
　「aの『[0,∞)で定義されたy=f (x)=xmn 』による逆像」f−1(a)に属す。[∵(2-2)]

・つまり、任意の正の実数a、自然数m,n に対して、
　　　  ( m
) ∈　[0,∞)　　
n
 a
　
　　　  ( m
) ∈　f−1(a)　…(4)
n
 a


・ところが、(1-2)(1-3)で明らかにされたように、
　　任意の正の実数a、任意の自然数m,nに対して、f−1(a) ＝  {
mn

 a   }
　つまり、
　　任意の正の実数a、自然数m,n に対して、
　　　「aの『[0,∞)で定義されたy=f (x)=xmn 』による逆像」f−1(a)に属すのは、
　　　　　　　　　　　　　　　　　　　　[0,∞)に存在する一個の実数  mn

 a  だけであって、
　　　
　　　　[0,∞)に存在する一個の実数  mn

 a  のほかには、
　　　　　　　　　　「aの『[0,∞)で定義されたy=f (x)=xmn 』による逆像」f−1(a)に属す実数は存在しない。

・したがって、　(1-2)(1-3)で明らかになったこの事実と、(4)から、
　　任意の正の実数a、自然数m,n に対して、
　　　　　　　　
 m
　＝　

　　　　 n
 a
mn
 a
　　となることがわかる。


→[累乗根の性質に戻る]

→[トピック一覧:べき関数]
→総目次


正の分数を指数とする累乗の定義、「『冪関数による像』の冪関数による逆像」としての「n乗のm乗根」

定義

 ・正の実数a,自然数m,自然数nに対して、
　　「aの(m/n)乗」am/n　とは、「『aのm乗』のn乗根」のことを指す。
・すなわち、
　　　　am/n=  am
　＝　(am)1/n　

・am/nの性質：約分に対して不変 /am/n＝(am)1/n＝(a1/n)m 　
　


[文献−解析]

　・赤攝也『実数論講義』§7.1定理7.1.1-2;補題(pp.204-5):証明つき。
　・吉田栗田戸田『昭和63年3/31文部省検定済　高等学校基礎解析』啓林館、2章1指数の拡張(p.42);.
　・小平『解析入門I』§2.3-a) (p.89):有理数指数での表現。

【関連事項】

　・拡張：正負の分数を指数とする累乗の定義/　




解説

 ・そもそも、「am/n」が表す
　　　 　「『aのm乗』のn乗根」 am 
　とは、どういった事態を指しているのだろうか？
　n乗根の定義まで遡って、捉えかえしてみると・・・

[step0:設定]

「『aのm乗』のn乗根」 am 
　は、　　　
　二つの1変数関数
　　　・[0,∞)で定義された冪関数y=f(x)=xm (mは自然数)のグラフ
　　　・[0,∞)で定義された冪関数y=g(x)=xn (nは自然数)のグラフ 
　を設置した下記平面のなかで、考えることができる。

　　　 ｎ乗のm乗根の意味step0

[step1:設定]
　　　
「『aのm乗』のn乗根」 am 
　における「正の実数a」とは、　　　
　この平面上、下記の「x軸上の点」で表される実数としよう。　

n乗のm乗根の意味step1　

[step2: amが指すこと]

　すると「『aのm乗』のn乗根」 am 
　における  am は、　　　
　 冪関数f によるaの像 f(a)であるから、
　下図のように、y軸上にプロットできる。

m乗のn乗根の意味step2

[step3: amのn乗根が指すこと]


・「実数yのn乗根」 y 
　(nは自然数)　とは、　　　
　　　　　正の実数yの『[0,∞)で定義された累乗関数y=g (x)=xn 』による逆像に唯一つ属す『正の実数』
　を指す記号だった。

・すると「『aのm乗』のn乗根」 am 
　(n,mは自然数)　とは、　　　
　　　　　正の実数amの『[0,∞)で定義された累乗関数y=g (x)=xn 』による逆像に唯一つ属す『正の実数』
　を指す記号だ、ということになる。

・ところが、step2で見たように、
　　amは、冪関数f によるaの像 f(a)として、平面上にその位置を与えられたのだった。

・このことも加味すると、
　「『aのm乗』のn乗根」 am 
　(n,mは自然数)　とは、　　　
　　　『[0,∞)で定義された冪関数y=f(x)=xm によるaの像』の『[0,∞)で定義された冪関数y=g (x)=xn 』による逆像
　　　　　　g-1( f(a) ) 
　　　　に唯一属す『正の実数』に他ならない。

・したがって、
　「『aのm乗』のn乗根」 am 
　(n,mは自然数)　は、　　　
　下図のように、　g-1( f(a) ) に唯一属す『正の実数』として、x軸上にプロットできる。

・これが、「am/n」が表す「『aのm乗』のn乗根」 am 
　の正確な事態である。　
　

m乗のn乗根の意味step3

→[トピック一覧:べき関数]
→総目次

「n乗のm乗根」「正の分数を指数とする累乗」の性質
　 累乗根の以下の性質は、有理数指数の累乗、有理数指数の指数法則を基礎付ける。

1.

 ・任意の正の実数a,任意の自然数m,n,tに対して、
　　　　  am
　＝　
nt  amt

・分数を指数とする累乗を用いて言い直すと、
　　任意の正の実数a,任意の自然数m,n,tに対して、am/n = a (mt)/(nt) 　
・つまり、
　　正の分数を指数とする累乗は、
　　指数として使われている分数の約分に関して不変。

※なぜ？→証明　

[文献]

　・赤攝也『実数論講義』§7.1定理7.1.1:証明つき。

2.

 ・正の実数a,自然数m,n,r,s に 対して、
　　　m/n＝r/s ならば、　 am
 　＝　
 s ar
・分数を指数とする累乗を用いて言い直すと、
　　任意の正の実数a,任意の自然数m,n,r,s に対して、
　　　　m/n＝r/s ならば、 　am/n = ar/s 　
・つまり、
　　正の有理数指数の累乗は、
　　有理数の分数としての表し方によらず、一意。
※なぜ？　
　・1.より、任意の正の実数a,任意の自然数m,n,r,s に 対して、
　　　　　　　 n
 am
 　＝　
 ns ams

　　　　　　　 s
 ar
 　＝　
 sn arn
　・任意の自然数m,n,r,s に 対して、m/n＝r/s ならば、ms=rn.　
　・上記2点より、
　　任意の正の実数a,任意の自然数m,n,r,s に 対して、　　　
　　　m/n＝r/s ならば、　 n
 am
  ＝
ns ams
 ＝
sn
arn  ＝
s ar

→[n乗のm乗根の性質冒頭へ戻る]　





[文献−解析]

　・赤攝也『実数論講義』§7.1定理7.1.2:1より証明。
　・吉田栗田戸田『昭和63年3/31文部省検定済　高等学校基礎解析』啓林館、2章1指数の拡張(p.42):一例で説明。6.を使う
　・小平『解析入門I』§2.3-a) (p.89):有理数指数での表現。指数法則を利用





3.

 ・任意の正の実数a,任意の自然数m,nに対して、
　　　　  n
 am
＝ (
n a )
 m
・分数を指数とする累乗を用いて言い直すと、
　任意の正の実数a,任意の自然数m,nに対して、
　　　am/n ＝ (am)1/n ＝ (a1/n)m
・つまり、
　任意の正の実数a,任意の自然数m,nに対して、
　　　分数を指数とする累乗am/n は、  n
 am
のみならず (
n a )
 m
も表している。

→[n乗のm乗根の性質冒頭へ戻る]　




[文献−解析]

　・赤攝也『実数論講義』§7.1補題(iv)(p.205):証明つき。
　・吉田栗田戸田『昭和63年3/31文部省検定済　高等学校基礎解析』啓林館、2章1指数の拡張(p.41):証明なし。いきなり「累乗根について次のことが成り立つ」




※なぜ？

[step0:累乗関数と累乗根の性質の確認]

　・任意の自然数n に対して、
　　『[0,∞)で定義された累乗関数y=f(x)=xn 』は、
　　　　　　　単射であって、[0,∞)を値域とする。…(0-1)
　・任意の正の実数y,任意の自然数n に対して、
　　yは「『[0,∞)で定義されたy=f(x)=xn』の値域」[0,∞)に属しているから、
　　(0-1)より、
　　yの『[0,∞)で定義されたy=f(x)=xn』による逆像 f-1(y)＝{x∈[0,∞)|y＝f (x)}は、
　　　　[0,∞)上に存在する1個の実数　
y
だけからなる。

　　つまり、
　　任意の正の実数y,任意の自然数n に対して、
　　　　　　　　　　 y   　∈[0,∞)であって、

　　　　　　　　　　　f−1(y)  ＝　  {
y   } 　…(0-2)　

　・このことは、
　　　[0,∞)上に存在する1個の実数　
y
のほかに、
　　　　　　　　　　　　　f−1(y) に属す実数が、存在しない
　　　ことを意味している。　　　　　　　　　　　　　　…(0-3)　









[step1:累乗関数と累乗根の性質からamの累乗根について言えること]


　・任意の正の実数a,任意の自然数mに対して、am＝aa…a>0　…(1-1)
　　　　　　∵　a>0であって、am＝aa…aだから、実数 の積の正負の性質より。

　・(0-2)と(1-1)より、
　　　任意の正の実数a、任意の自然数nに対して、
　　　　　「amの『[0,∞)で定義されたy=f(x)=xn』による逆像」
　　　　　 f−1(am)＝{x∈[0,∞)|am=f(x)}
　　　　は、
　　　　[0,∞)上に存在する1個の実数　
am
だけからなる。

　　　　　つまり、　 am  　∈　[0,∞)　であって、

　　　　　　　　　　　f−1(am)  ＝　  {
am   } 　　…(1-2)　　

　・このことは、
　　　[0,∞)上に存在する1個の実数　
am
のほかに、
　　　　　　　　　　　　　f−1(am)  に属す実数が、存在しない
　　　ことを意味している。　　　　　　　　　　　　　　…(1-3)　
    　　　　　　　　　　　　　

[step2:指数法則から言えること]

　・任意の正の実数a,任意の自然数m,nに対して、
　　　　　  ((
 a  )
 m
) n
   

　　　　　　＝ (
n a )
 mn
  
 ∵指数法則2

　　　　　　＝ ((
n a )
 n ) m  ∵指数法則2 　
　　　　 　　＝am　　　　　　　　∵累乗根の性質0
　・要するに、  ((
 a  )
 m
) n
  ＝am …(2-1)

　・このことは、
　　任意の正の実数a,任意の自然数m,nに対して、
　　  (
 a  )
 m
  の『[0,∞)で定義されたy=f(x)=xn』による像がamであること 

　　　　　　　　　　　　　　　  f(
 (
 a  )
 m
 )  ＝am　　　　　…(2-2) 
　　を意味する。

[step3]

　・任意の正の実数a、任意の自然数n に対して　
　　　　　　　(0-2)より、  a  　≧0
 　　…(3-1)　

　・(3-1)と実数 の積の正負の性質より、
　　任意の正の実数a,任意の自然数m,nに対して、  (
 a  )
 m
  ≧0　…(3-2)

　・このことは、
　　任意の正の実数a,任意の自然数m,nに対して、  (
 a  )
 m
  が[0,∞)に存在する…(3-3)
　　ということを意味する。




[step4:結論]

　・任意の正の実数a、任意の自然数m,nに対して、 (
 a  )
 m
  は、[0,∞)に存在して、[∵(3-2),(3-3)]
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　「amの『[0,∞)で定義されたy=f(x)=xn』による逆像」f−1(am) に属す[∵(2-2)]

　・つまり、任意の正の実数a、任意の自然数m,nに対して、
　　　　　　　　　　　 (
 a  )
 m
  ∈  [0,∞)であって、

　　　　　　　　　　　 (
 a  )
 m
  ∈  f−1(am)　　　　　　…(3)
 
　・ところが、(1-2)(1-3)で明らかにされたように、　
　　　　任意の正の実数a、任意の自然数m,nに対して、f−1(am) ＝  {
am   }

　　つまり、任意の正の実数a、任意の自然数m,nに対して、
　　「amの『[0,∞)で定義されたy=f(x)=xn』による逆像」f−1(am)に属すのは、
　　　[0,∞)上に存在する1個の実数　
am
だけであって、

　　　[0,∞)上に存在する1個の実数　
am
のほかには、
　　　「amの『[0,∞)で定義されたy=f (x)=xn』による逆像」f-1(an)に属す実数
　は存在しない。

・したがって、　(1-2)(1-3)で明らかになったこの事実と、(3)から、
　　　任意の正の実数a、任意の自然数m,n に対して、　 am ＝ (
 a )
 m
　となることがわかる。

→[n乗のm乗根の性質冒頭]　

[以下は、初期の草稿]
※なぜ？
　[step0:設定の把握]
　　左辺　 n
 		am
 		　(a:正の実数,m,n:自然数)　は、　
　　　a, am に対して、
　　下図のように、関係づけられた(→「『aのm乗』のn乗根」の説明)。

　[step1]
　　　累乗根の性質0より、
　　　任意の正の実数a,任意の自然数nに対して、a＝ (
n a )
 n


　[step2]
 　任意の正の実数a,任意の自然数m,nに対して、
　　am＝ ((
n a )
 n
) m
∵step1

　　　　＝ (
n a )
 mn
  
 ∵指数法則2

　　　　＝ ((
n a )
 m
) n
∵指数法則2

　[step3]
 　任意の正の実数a,任意の自然数m,nに対して、
　 n

　　　　  n
 am
＝ ((
n a )
 m
)
 n      ∵step2

　　　　　　　  ＝ (
n a )
 m
　∵累乗根の性質0



→[「n乗のm乗根」「分数を指数とする累乗」の性質へ戻る]






1の証明

証明したい命題の確認
　・正の実数a,自然数m,n,tに対して、
　　　　  am
 		　＝　
nt  amt
　・つまり、正の実数a,自然数m,n,tに対して、am/n = a (mt)/(nt) 　　
　　
step0 : 設定の把握

　左辺　 am
　(a:正の実数,m,n:自然数)　は、　
　a, am に対して、
　下図のように、関係づけられた(→「『aのm乗』のn乗根」の説明)。

[文献]

　・赤攝也『実数論講義』§7.1定理7.1.1:証明つき(p.204)。


※拡張：mが負の整数であるケース　





step1:

　ここで、  am
 (a:正の実数,m,n:自然数)　を、bで表すことにする。　

　つまり、b =   am
　(a:正の実数,m,n:自然数)…(1)



ｍ乗のn乗根の公式1

step2:
　すると、n乗根の定義より、
　(1)のもとで、am=bn　(a:正の実数,m,n:自然数) が成立する…(2)

「m乗のn乗根」公式1

step3:
　・am=bn　ならば、任意の自然数tに対して、　amt=bnt　。（∵指数法則2'）
　・したがって、step2より、
　　(1)のもとで、amt=bnt　(a:正の実数,m,n,t:自然数) が成立することになる。…(3)




step4:
　・累乗根の定義により、
　　　　amt=bnt　ならば、  　b　＝　
nt  amt

　・したがって、step3より、
　　　　 (1)のもとで、  　b　＝　
nt  amt 　　が成立することになる。…(4)







step5:
　
　(4)より、b =   am
のもとで、b＝ nt　
 amt が成立するというのだから、
　
　b =   am
　のもとで、
　
　　　　b =   am
= nt　
 amt

　である。
　つまり、正の実数a,自然数m,n,tに対して、
　　　　  am
 		　＝　
nt  amt




→[「n乗のm乗根」「分数を指数とする累乗」の性質へ戻る]



→[トピック一覧:べき関数]
→総目次

自然数指数の冪関数（累乗関数）と全単射
→(-∞,∞)で定義された冪関数について、単射/全射/全単射を検討　
→[  0,∞)で定義された冪関数について、単射/全射/全単射を検討　
→(-∞, 0)で定義された冪関数について、単射/全射/全単射を検討　 		※定義の確認→自然数指数の冪関数//1変数関数が単射/全射/全単射　
※具体例→y=xについて/y=x2について/y=x3について
※一般化→有理数指数の冪関数について/実数指数の冪関数について

(-∞,∞)で定義された自然数指数の冪関数について、単射/全射/全単射を検討
　→　単射の検討　〜　(-∞,∞)で定義された自然数指数の冪関数について。
　→　全射の検討　〜　(-∞,∞)で定義された自然数指数の冪関数について。
　→全単射の検討　〜　(-∞,∞)で定義された自然数指数の冪関数について。
　→自然数指数の冪関数全般の単射/全射/全単射の検討に戻る

※(−∞,∞）で定義された自然数指数の「べき関数」とは？



y=x  
　　　　　　　　　

べき関数のグラフ（指数を自然数に限定）
[単射の検討〜(-∞,∞)で定義された自然数指数の冪関数について]
・R＝(−∞,∞）で定義された自然数指数の「べき関数」「累乗関数」　
　 　　　y=f (x)=xa  (aは自然数)
　は、
　　　aが奇数ならば 単射。
　　　aが偶数ならば 単射にならない。　

※な ぜ？
　・aが奇数ならば、
　　　　y=f (x)=xa は(−∞,＋∞)で狭 義単調となって、
　　　　下図をいじるとわかるように、
　　　　ど のように、実数yを 選んでも、実数yのfによる逆像 f−1(y)は 「1個の実数」
　　　　となるから、単射[→狭義単調ならば単射]。 　　
y=f(x)=x による　y= の逆像　f-1(　　)

[図]
　　　べき関数による逆像

　 ・「y=f (x)=xa」 のaが偶数な らば、
　　　下図をいじるとわかるように、
　　　任意の正の実数yに対して、実数yのfによる逆像 f−1(y)は 「2個の実数」からなるので、
　　　y=f (x)=xa は、単射の 定義を満たさない。
　　
y=f(x)=x による　y= の逆像　f-1(　　)

[図]
　　　べき関数による逆像
　
[全射の検討〜(-∞,∞)で定義された自然数指数の冪関数について]
・R＝(−∞,∞）で定義された「べき関数」「累乗関数」　
　 　　　y=f (x)=xa  (aは自然数)
　は、
　　　aが奇数ならば、Rの上への全射（値域がR＝(−∞,∞）だから）。
　　　aが偶数ならば、Rの上への全射ではないが、
　　　　　　　　　　[0,∞)の上への全射ではある。　




[全単射の検討〜(-∞,∞)で定義された自然数指数の冪関数について]
・R＝(−∞,∞）で定義された「べき関数」「累乗関数」　
　 　　　y=f (x)=xa  (aは自然数)
　は、
　　　aが奇数ならば、 Rの上への全単射
　　　　　　　　　　　　（(−∞,＋∞)で狭義単調、値域がR＝(−∞,∞）だから）。
　　　aが偶数ならば、全単射でない（単射にならない）。

[0,∞)で定義された自然数指数の冪関数について、単射/全射/全単射を検討
　→　単射の検討　〜　[0,∞)で定義された自然数指数の冪関数について。
　→　全射の検討　〜　[0,∞)で定義された自然数指数の冪関数について。
　→全単射の検討　〜　[0,∞)で定義された自然数指数の冪関数について。
　→自然数指数の冪関数全般の単射/全射/全単射の検討に戻る
[単射の検討〜[0,∞)で定義された自然数指数の冪関数について]

・[0,∞)で定義された「べき関数」「累乗関数」　
　 　　　y=f (x)=xa  (aは自然数)
　は、aが奇数でも偶数でも、 単射になる。




【文献】

　・上野健爾『岩波講座現代数学への入門7-8：代数入門1』定理2.35(pp.67-68)。
　・加藤十吉『微分積分学原論』命題3.5(p.28)








※な ぜ？→　　[0,∞)で定義された「y=f (x)=xa (aは 自然数)」は[0,∞)で狭 義単調だから、
　　　　　　下図をいじるとわかるように、
　　　　　　ど のように、実数yを 選んでも、
　　　　　　　　　・実数yのfによる逆像 f−1(y)が 「1個の実数」からなる
　　　　　　　　　または、
　　　　　　　　　・実数yのfによる逆像 f−1(y)は空集合　
　　　　　　よって、[0,∞)で定義された「y=f (x)=xa (aは自然数)」は単射[→証明「狭義単調ならば単 射」]。
　　


y=f(x)=x によるy= の逆像　f-1(　　)
[図]

　　　　
　　　べき関数による逆像
[全射の検討〜[0,∞)で定義された自然数指数の冪関数と]

・[0,∞)で定義された「べき関数」「累乗関数」　
　 　　　y=f (x)=xa  (aは自然数)
　は、aが奇数でも偶数でも、Rの上への全射ではないが、
　　　　　　　　　　[0,∞)の上への全射ではある。
[全単射の検討〜[0,∞)で定義された自然数指数の冪関数と]

・[0,∞)で定義された「べき関数」「累乗関数」　
　 　　　y=f (x)=xa  (aは自然数)
　は、aが奇数でも偶数でも、[0,∞)の上への全単射。（Rの上への全単射ではない）

(−∞,0]で定義された自然数指数の冪関数について、単射/全射/全単射を検討
　
[単射の検討]

・(−∞,0]で定義された自然数指数の「べき関数」「累乗関数」　
　 　　　y=f (x)=xa 
　は、aが奇数でも偶数でも、 単射になる((−∞,0]で狭義単調だから[→証明])。

[全射の検討]

・(−∞,0]で定義された自然数指数の「べき関数」「累乗関数」　
　 　　　y=f (x)=xa 
　は、
 　　　aが奇数ならば、Rの上への全射ではないが、(−∞,0]の上への全射　　
　　　aが偶数ならば、Rの上への全射ではないが、[0,∞)の上への全射。

[全単射の検討]

・(−∞,0]で定義された自然数指数の「べき関数」「累乗関数」　
　 　　　y=f (x)=xa 
　は、
 　　　aが奇数ならば、(−∞,0]の上への全単射。（Rの上への全単射ではない）
　　　aが偶数ならば、[0,∞)の上への全単射。（Rの上への全単射ではない）

→[トピック一覧:べき関数]
→総目次


自然数指数の冪関数（累乗関数）の逆関数
べき根radical root（累乗根）の定義

　→(−∞,∞）で定義された自然数指数の「べき関数」「累乗関数」について
　→[0,∞)で定義された自然数指数の「べき関数」「累乗関数」について

[1]
(−∞,∞）で定義された自然数指数の「べき関数」の逆関数について。

[ベキ関数の逆関数の存在]

・R＝(−∞,∞）で定義された自然数指数の「べき関数」　
　 　　　f (x)=xn  （nは自然数）
　の逆関数は、
　　・nが奇数ならば、存在する。
　　・nが偶数ならば、存在しない。
※なぜ？
　・nが奇数ならば、
　　　　f (x)=xnは、R＝(−∞,∞）で狭義単調関数であるから（∵）、
　　　　単射となって、（∵）
　　　　逆関数の存在が保証される（∵）。
　　実際、

[文献-タイプA:[0,∞)で定義されたべき関数による逆像が累乗根]

　・小平『解析入門I』§2.3-a) (p.89);「巾関数」
　・ 松坂『解析入門1』3.2E-例(p.113)：n乗根関数（n乗根の定義）も。
　・赤攝也『実数論講義』§6.5定義6.5.3(p.197):。
　・黒田『微分積分学』3.3.4-例3.18(p.107);

[文献-タイプB:Rで定義されたべき関数による逆像が累乗根]

　・『基礎解析』p.40.
　・『岩波数学入門辞典』平方根(p.543)べき根(p.546)
※1変数関数の「逆関数（の存在）」定義
※自然数指数の冪関数の逆関数の具体例：y=x3/y=x2/y=x/定数値関数　
※一般化された冪関数の逆関数：　　　
y=x

　　のグラフは、下図のようになる。
　　　べき関数のグラフ（指数を自然数に限定）
　・nが偶数な らば、
　　　f (x)=xnは単射にならないから、逆関数は存在しない（∵）。
　　　実際、
y=x

　　　のグラフは、下図のようになる。
　　　べき関数のグラフ（指数を自然数に限定）

[ベキ関数の逆関数の定義域]

 ・R＝(−∞,∞）で定義された自然数指数の「べき関数」f (x)=xn  のnが奇数であるとき（つまり、fに逆関数が存在するとき）、
　「f (x)=xn」の値域は、R＝(−∞,∞）だから、
　「f (x)=xn（nは奇数）」の逆関数 x=f-1(y)は、R＝(−∞,∞）で定義される。

[ベキ関数の逆関数の表記]

 ・R＝(−∞,∞）で定義された自然数指数の「べき関数」　f (x)=xn のnが奇数であるとき（つまり、fに逆関数が存在するとき）、
 　「実数yの『f (x)=xn の逆関数』による像」すなわち、「実数yの『f (x)=xn』による逆像」　f-1(y)　は、
　　記号　  y 
　または、　y1/n 　　　　
　　で表される。
　・したがって、　R＝(−∞,∞）で定義された「f (x)=xn（nは奇数）」の逆関数 x=f-1(y)　は、　
　　　　x=f-1(y)＝  y  　または、x=f-1(y)＝y1/n 　
　　と、表されることになる。

[逆関数のグラフ]

・ 「Dで定義された1変数関数y=f(x)の逆関数」x ＝ f -1 (y)＝『yの式』
　　について、x,yを入れ替えて
　　　　　y ＝『xの式』
　　という形にするのが慣例。
　　この慣例にしたがうと、
　　R＝(−∞,∞）で定義された自然数指数の「べき関数」「累乗関数」　「f (x)=xn（nは奇数）」の逆関数 は、
　　y=  x 
　　となる。
・R＝(−∞,∞）で定義された自然数指数の「べき関数」「累乗関数」　「f (x)=xn（nは奇数）」の逆関数 のグラフは、
　x,yを入れ替えず、
　　　　　x=  y 
　と表した場合、「f (x)=xn（nは奇数）のグラフ」と同一（見方を逆にするだけ）、
　x,yを入れ替えて、
　　　　　y=  x 
　と表した場合、直線y=xについて、「f (x)=xn（nは奇数）のグラフ」と線対称になる。

　[図]
　

[2]
[0,∞)で定義された自然数指数の「べき関数」「累乗関数」について。

[逆関数の存在]

・[0,∞)で定義された自然数指数の「べき関数」「f (x)=xn  (nは自然数)」の逆関数は、
　　nが奇数でも偶数でも、存在する。
※なぜ？
　　[0,∞)で狭義単調だから、単射になって逆関数の存在が保証される（∵）。

　　実際、[0,∞)で定義された自然数指数の「べき関数」
y=x

　　のグラフは、下図のようになる。

[0,∞)で定義されたべき関数のグラフ（指数を自然数に限定）

[逆関数の定義域]

・[0,∞)で定義された自然数指数の「べき関数」「累乗関数」「f (x)=xn  （nは自然数）」の値域は、[0,∞)だから、
　「f (x)=xn(nは自然数)」の逆関数 x=f-1(y)は、[0,∞)で定義される。

[逆関数の表記]

　・「正の実数yの『[0,∞)で定義されたf (x)=xn の逆関数』による像」
　　　　　　すなわち、「正の実数yの『[0,∞)で定義されたf (x)=xn』による逆像」　f-1(y)　
　　　　
　　は、記号　  y 
　または、　y1/n 　　で表される。　　
　・したがって、
　　[0,∞)で定義されたf (x)=xnの逆関数 x=f-1(y)　は、　
　　　　x=f-1(y)＝  y 
　または、x=f-1(y)＝y1/n 　
　　で表される。

[逆関数のグラフ]

・[0,∞)で定義された自然数指数の「べき関数」「累乗関数」「f (x)=xn(nは自然数)」の逆関数 のグラフは、
　　x,yを入れ替えず、
　　　　　x=  y 
　　と表した場合、「y=f (x)=xn (nは自然数)のグラフ」と同一（見方を逆にするだけ）、
　　x,yを入れ替えて、
　　　　　y=  x 
　　と表した場合、直線y=xについて、「y=f (x)=xn (nは自然数)のグラフ」と線対称になる。

　[図]

→[トピック一覧:べき関数]
→総目次

自然数指数の冪関数（累乗関数）の極限
　  ・R＝(−∞,∞）で定義された「べき関数」 f (x)=xa (aは自然数) は、
　　　　どんな実数x0に対しても、　f(x)→ x0a (x→x0)

※なぜ？
　[step1]
　・y=f1(x)=xの極限の性質より、
　　y=f1(x)= xは、
　　どんな実数x0に対しても、　f1(x)→x0 (x→x0)。
　[step2]
　・「関数どおしの積」の極限は、「関数の極限」どおしの積となるという定理と、
　　step1で得られた「f1(x)の極限値」より、
　　　　f1(x)2→x02 (x→x0)
　・したがって、f 2(x)=f1(x)2= x2は、
　　　　どんな実数x0に対しても、　f2(x)→x02(x→x0)　。
　[step3]
　　・「関数どおしの積」の極限は、「関数の極限」どおしの積となるという定理と、
　　　　step1で得られた「f1(x)= xの極限値」,
　　　　step2で得られた「f2(x)= x2の極限値」より、
　　　f 3(x)=f1(x)f2(x)= x3は、
　　　　どんな実数x0に対しても、　f3(x)→x03(x→x0)　。
　[step4]
　　・「関数どおしの積」の極限は、「関数の極限」どおしの積となるという定理と、
　　　　step1で得られた「f1(x)= xの極限値」,
　　　　step3で得られた「f3(x)= x3の極限値」より、
　　　f 4(x)=f1(x)f3(x)= x4は、
　　　　どんな実数x0に対しても、　f4(x)→x04(x→x0)　。
　　：
　[step a]
　　・「関数どおしの積」の極限は、「関数の極限」どおしの積となるという定理と、
　　　　step1で得られた「f1(x)= xの極限値」,
　　　　step(a-1)で得られた「fa-1(x)= xa-1の極限値」より、
　　　f a(x)=f1(x)fa-1(x)= xaは、
　　　　どんな実数x0に対しても、　fa(x)→x0a(x→x0)　。
　




【文献−解析】

　・赤攝也『実数論講義』§6.3例4(p.176):
　　　　　　連続性を、直接「ε-δ論法」から証明したもののなかで。
　・吉永『初等解析学:実数+イプシロンデルタ+積分』例3.1.5(p.109）:
　　　　　・多項式関数一般に関して。
　　　　　・定数関数の極限、f(x)=xの極限と、関数の極限の和積による証明つき。
　・黒田『微分積分学』3.3.2-例3.16(p.102):「任意の多項式はRで連続」。
　　・証明として、
　　　定数関数とf(x)=xがRで連続だから、連続関数の和差積・定数倍も連続関数より。

【関連事項】


　・1変数関数の極限定義
　・1変数関数の具体例の極限：
　　　定数値関数/y=x/比例/一次関数/反比例/二次関数/べき関数
　　　指数関数/対数関数/絶対値関数/三角関数/ガンマ関数




→[トピック一覧:べき関数]
→総目次


自然数指数の冪関数（累乗関数）の連続性
　 ・R＝(−∞,∞）で定義された「べき関数」 f (x)=xa (aは自然数) は、
　　　　　R＝(−∞,∞）上の連続関数。
※なぜ？
　・f (x)=xaという定義より、どんな実数x0に対しても、f(x0)=x0a
　・f (x)=xaの極限の性質より、どんな実数x0に対しても、f(x)→ x0a (x→x0)
　・以上二点より、どんな実数x0に対しても、　f(x)→f(x0) (x→x0)　
　　つまり、R＝(−∞,∞）で定義された「べき関数」 f (x)=xa (aは自然数) は、
　　　　　　　　　どんな実数x0においても、連続性の定義を満たす。
　　したがって、
　　　R＝(−∞,∞）で定義された「べき関数」 f (x)=xa (aは自然数) は、
　　　　　R＝(−∞,∞）上の連続関数。　　　
 　

[文献-自然数を指数とするべき関数]

　・赤攝也『実数論講義』§6.5定理6.5.1(p.187):。

[以下未確認]
　・黒田『微分積分学』3.3.2-例3.16(p.102):「任意の多項式はRで連続」。
　　　→証明：定数値関数の連続性・y=f(x)=xの連続性、連続関数の和積定数倍も連続
　・吉永『初等解析学:実数+イプシロンデルタ+積分』例3.2.7(p.115）:多項式一般。
　　　　　　　　・証明：多項式関数の極限の性質より。
　・小林昭七『微分積分読本:1変数』第2章-1(p.38):多項式一般。証明:
　　　→証明：定数値関数の連続性・y=f(x)=xの連続性、連続関数の和積も連続
　
※1変数連続関数の定義
※1変数関数の具体例の連続性：
　　　定数値関数/y=x/比例/一次関数/反比例/二次関数/べき関数
　　　指数関数/対数関数/絶対値関数/三角関数/ガンマ関数

→[トピック一覧:べき関数]
→総目次


（reference）

高木貞治『解析概論改訂第3版』岩波書店、1983年、pp.105-108;
和達三樹『理工系の数学入門コース1・微分積分』岩波書店、1988年、pp.20-21。
青本和彦『岩波講座現代数学への入門：微分と積分1』岩波書店、1995年、p.84:高階導関数、p.93:凸性、p.110:原始関数。
黒田成俊『21世紀の数学1:微分積分学』共立出版株式会社、2002年、pp.171-173。
住友洸『大学一年生の微積分学』現代数学社、1987年、p.122.
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.115-6.