ガンマ関数
【トピック一覧】
・定義：ガンマ関数
・定理：ガンマ関数の基本的な性質 /
【関連ページ：1変数関数の広義積分について】
前：広義積分の定義(有限区間における非有界関数・無限区間において)・性質・向き付き広義積分・
積分関数(不定積分)・解析学の基本定理・収束条件
次：
cf. 1変数関数の定積分、2変数関数の広義積分、n変数関数の広義積分
→参考文献一覧・総目次
定義：ガンマ関数
[矢野田代『社会科学社のための基礎数学』pp.120-121;小平『解析入門I』188-189;吹田新保『理工系の微分積分学』118-9; 片山『微分積分学』122-123.]
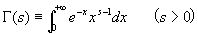
sがプラスなら、右辺の広義積分(オイラーの第2種積分)は収束する(→数行下で説明)。
右辺の広義積分をsの関数とみなし、
sがプラスである場合にのみ、これをガンマ関数として定義する。
(ガンマ関数が収束することの証明)
[小平『解析入門I』pp.188-189;吹田新保『理工系の微分積分学』118-9; Fischer.Intermediate Real Analysis, 717-718.]
方針:
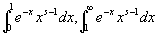
のそれぞれがs>0という条件下で収束することを示す。
この二つがともに収束すれば、広義積分
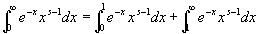
も定義され、収束することになる。
(step1)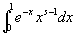 
の収束の証明：
(i) 0< s <1のとき
まず、被積分関数f (x)= e −x x s−1の閉区間[0,1]における性格を把握。
被積分関数を分かりやすく書くと、
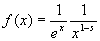
ここでは、0≦x≦1かつ0< s <1(ゆえに0< 1−s <1)の条件下のみの検討であることに注意。
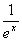
は、ここでの、0≦x≦1の条件下では、全ての点で連続であり、また、特異点も存在しない。
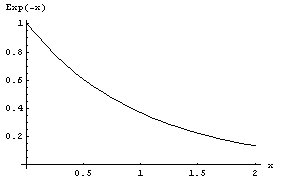
図1: e −x をプロットしたグラフ
しかし、
は、0＜x≦1かつ0< s <1(ゆえに0< 1−s <1)の条件下では、
全ての点で連続であり、特異点も存在しないものの、
x＝0という一点が特異点となる。
よって、この二つの関数の積であるf(x)は、連続関数の性質より、左半開区間(0,1]で連続関数となる。
しかし、x＝0という一点は特異点となる。
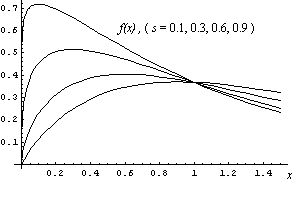
図２： sを0.1, 0.3, 0.6, 0.9とした際の、
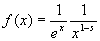
をプロットしたグラフ。
以上から、x＝0が特異点となるので、
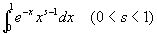
は、定積分ではなく、広義積分として考えなければならないことが分かった。
つまり、厳密には以下のような右極限として書かなければならない。
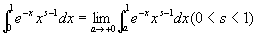
次に、この広義積分が0< s <1という条件下で収束するか否かを検討する。
定理により、
左半開区間(0,1]において、被積分関数f(x)についての不等式
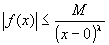
を満たす0<λ<1なるλ、定数Mがそれぞれ一つでも存在するならば、
すなわち、
|e−xxs−1|≦M/xλ …※
を満たす0<λ<1なるλ、定数Mの存在をそれぞれ一つでも確認できさえすれば、
左半開区間(0,1]において、
この広義積分
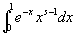
が絶対収束するといってよい。
果たして、※を成立させるλ(0<λ<1)、Mは存在するのか？
|e−xxs−1|
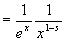∵図2より0＜x≦1かつ0< s <1(ゆえに0< 1−s <1)の条件下では、常にプラス。
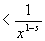∵図1より、0<x≦1では、0<1/ex<1 となるから。
つまり、|e−xxs−1|<1/x1−s
よって、
※を満たすλ=1-s (0< 1−s <1に注意)、定数M＝１の存在が確認されたことになる。
ゆえに、
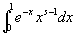
は収束する。
(ii) s ≧1のとき
まず、被積分関数f (x)= e −x x s−1 (s≧1)の閉区間[0,1]における性格を把握。
被積分関数を分かりやすく書くと、
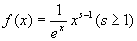
ここでは、0≦x≦1 かつ 1 ≦ sという条件下のみの検討であることに注意。
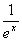
は、ここでの、0≦x≦1の条件下では、全ての点で連続であり、特異点も存在しない。→図1
x s−1も、0≦x≦1 かつ 1 ≦ sという条件下では、全ての点で連続であり、特異点も存在しない。
よって、f(x)は二つの連続関数の積となるから、連続関数の性質より、閉区間[0,1]で連続関数となる。
閉区間上の連続関数はリーマン可積分だから、
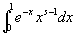
は、定積分として存在する。
これをあえて広義積分風にいえば、「収束する」ということになる。
以上、(i)(ii)の検討を合せて考えると、すべてのs>0について、
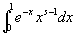
は、収束するといえる。
(step2)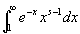 
の収束の証明：
定理より、
被積分関数e−xxs−1 ( s > 0 )が、無限区間[1,∞)で連続で、
「無限区間[1,∞)において、 xλ| e−xxs−1|≦M …(※)
を満たす定数M、1<λなるλがそれぞれ一つは存在する」
ことが確認されさえすれば、
広義積分
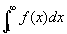
は絶対収束するといってよい。
果たして、(※)を満たすM、1<λなるλは存在するのか？
→確かに存在する。(※)を満たすM,λとして、たとえば、
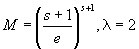
がある。
λ=2を(※)の左辺に代入し、無限区間[1,∞)における(※)左辺全体の動きを調べてみよう。
λ=2を代入した(※)左辺= x2| e−xxs−1|
= x2| e−xxs−1| ∵ここでの x≧1, s >0という条件下では、e−xxs−1>0
= e−xxs+1
まず、λ=2を代入した(※)左辺=e−xxs+1の1階の導関数を求める。
(e−xxs+1)'=(e−x)' xs+1+e−x(xs+1)' ∵積の微分
=(e−x)' xs+1+e−x(s+1)xs ∵
=−e−x xs+1+e−x(s+1)xs
∵e−x はg(y)=ey, y=f(x) =−xの合成関数g(f(x))だから、合成関数の微分則より、
e−x の導関数は、
g'( f(x) ) f'(x)= g'(−x )・(−1 )
= e−x・(−1 ) ∵指数関数の微分
= e−x xs+ (s+1−x )
ここでの x≧1, s >0という条件下では、常にe−x xs>0 なので、
λ=2を代入した(※)左辺の1階の導関数の符号は、(s+1−x )の正負によって決まる。
つまり、
1≦x<s+1で(e−xxs＋1)'>0、
x=s+1 で(e−xxs＋1)'=0、
s+1<x で(e−xxs＋1)'<0、
1階の導関数と関数の増減の関係から、
λ=2を代入した(※)左辺=e−xxs＋1(x≧1, s >0)は、
右半開区間[1, s+1]で狭義単調増加、x=s+1で最大値をとり、[s+1,∞)では狭義単調減少となることがわかる。
ちなみに、
e−xxs＋1の2階の導関数を求めると、
(e−xxs＋1)''= {e−x xs (s+1−x ) }'= {(s+1)e−x xs−e−x xs+1 }'
=((s+1)e−x xs)'−(e−x xs+1)'
=(e−x)' (s+1)xs + e−x ((s+1)xs)'−(e−x)' xs+1− e−x (xs+1)'
=−e−x(s+1)xs + e−x (s+1)sxs−1＋e−x xs+1− e−x (s+1) xs
=−e−xxs(s+1) + e−x xs−1(s+1)s＋e−x xs+1− e−x xs(s+1)
=e−x xs−1{−x(s+1)+(s+1)s+ x2−x (s+1) }
=e−x xs−1{−2x(s+1)+(s+1)s+ x2 }
=e−x xs−1{ x2−2 (s+1) x +s2+s }
x ≧1, s >0という条件下では、e−xx s−1>0 なので、
(e−xxs＋1)''の符号は、{ x2−2 (s+1) x +s2+s }の正負によって決まる。
この2次関数は、変形すると、(x−(s+1))2−(s+1)となることから、
x=s+1>1で最小値−(s+1)<−1をとる放物線。
2次方程式x2−2 (s+1) x +s2+s=0 の解は、
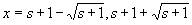
よって、
{ x2−2 (s+1) x +s2+s }>0、ゆえに(e−xxs＋1)''>0(狭義に(下に)凸)
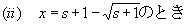
{ x2−2 (s+1) x +s2+s }＝0、ゆえに(e−xxs＋1)''=0
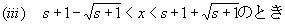
{ x2−2 (s+1) x +s2+s }<0、ゆえに(e−xxs＋1)''<0(狭義に凹=上に凸)
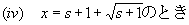
{ x2−2 (s+1) x +s2+s }＝0、ゆえに(e−xxs＋1)''=0
{ x2−2 (s+1) x +s2+s }>0、ゆえに(e−xxs＋1)''>0(狭義に(下に)凸)
ただし、sが十分に大きくなければ、(i)(ii)は、x ≧1の定義域に入らなくなることに注意。
というわけで、λ=2を代入した(※)左辺=e−xxs＋1(x≧1, s >0)は、x=s+1で最大値をとるが、
その最大値を計算すると、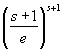 
よって、x≧1, s >0という条件下では、、
λ=2を代入した(※)左辺：
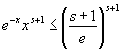
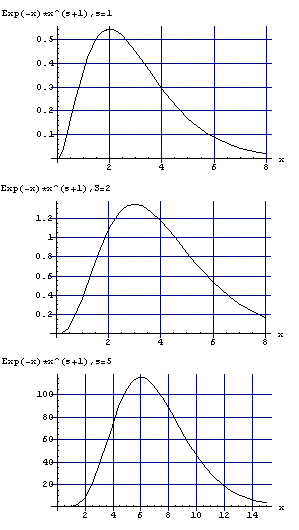
図3： sを1, 2, 5,とした際の、
λ=2を代入した(※)左辺=e−xxs＋1
をプロットしたグラフ。
以上から、(※)を満たすM、1<λなるλとして、少なくとも
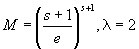
が存在することがわかった。
よって、定理より、x≧1, s >0という条件下では、
広義積分
は絶対収束するといえる。
(step 3)
step1,step2での検討結果から、
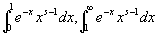
s>0という条件下でともに収束することが明らかになったので、
広義積分
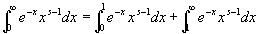
も定義され、収束すると結論できる。
定理：ガンマ関数の基本的な性質
[矢野田代『社会科学者のための基礎数学』pp.120-121;小平『解析入門I』pp.188-189;. ;吹田新保『理工系の微分積分学』118-9.]
1. Γ( s+1 )= sΓ( s ) ( s ＞ 0 )
次のように書いても同じ：Γ( s )=( s−1 ) Γ( s−1 ) ( s ＞ 1 )
2. Γ(n)=(n−1)! (n∈N)
3. Γ(1)=Γ(2)=1
4. Γ(s)は、s>0で連続、C∞級。[杉浦『解析入門』p.327.]
n階導関数は、
5. log Γ(x)は、x>0で凸関数。[杉浦『解析入門』p.327.]
定理：
[杉浦『解析入門』p.328.]
f:R=(0,+∞)→Rが、
任意のx>0に対し、
(1) f(x+1)=xf(x)
(2) f(x)>0でlogf(x)は凸関数
(3) f(1)=1
を満たすならば、
任意のx>0に対し、f(x)=Γ(x)
（reference）
日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年、66項ガンマ関数(pp.66-67)。
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.101-3.
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.118-9.例題として。
矢野健太郎・田代嘉宏『社会科学者のための基礎数学 改訂版』裳華房、pp.120-121.
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年 pp.188-189。
杉浦光夫『解析入門』岩波書店、1980年、pp.295-301:基本; pp.326-341:性質を詳しく。
高木貞治『解析概論 改訂第三版』岩波書店、1983年、p. 108:例題として。
青本和彦『岩波講座現代数学への入門：微分と積分1』岩波書店、1995年、pp.142-145。
片山孝次『微分積分学』(現代数学レクチャーズB-8)、培風館、1980年、pp. 122-123。
Fischer,Emanuel.Intermediate Real Analysis(Undergraduate
Texts in Mathematics),Springer-Verlag New York Heidelberg
Berlin,1983,pp.417-426.積分を用いないガンマ関数定義;
717-718:Γ関数の収束.726-735.積分によるガンマ関数・ベータ関数定義;