広義積分の収束条件
【トピック一覧】
・定義：収束・絶対収束・条件収束
・定理：コーシーの判定法/広義積分が絶対収束するための十分条件(その1 )/広義積分が絶対収束するための十分条件 (その2)
【関連ページ：1変数関数の広義積分について】
前：広義積分の定義(有限区間における非有界関数・無限区間において)・性質・向き付き広義積分・
積分関数(不定積分)・解析学の基本定理
次： ガンマ関数ベータ関数
cf. 1変数関数の定積分、2変数関数の広義積分、n変数関数の広義積分
→参考文献一覧・総目次
収束・絶対収束・条件収束：
[高木『解析概論』pp.106-107:証明つき; 吹田新保『理工系の微分積分学』p.117; Fischer, Intermediate Real Analysis,p. 721.]
1. ある広義積分が絶対収束するならば、、その広義積分は収束する。(∵広義積分に関する三角不等式)
しかし、ある広義積分が絶対収束していなくても、収束することもある。
（絶対収束は収束の十分条件であるが、必要条件ではない）
2. 収束しているが、絶対収束でない広義積分は、条件収束する conditionally convergent という。
定理:広義積分の収束についてのコーシーの判定法
Cauchy Criterion for Convergence of Improper Integrals
[高木『解析概論』pp.105-106;小平『解析入門I』184-185; 片山『微分積分学』118-121;杉浦『解析入門I』292;
住友『大学一年生の微積分学』124;Fischer, Intermediate Real Analysis, 719; Lang,Undergraduate Analysis280.]
→基礎となる定理： 関数の収束についてのコーシーの判定法、
以下、左半開区間/右半開区間/無限区間での広義積分に分けて、コーシーの収束判定条件を示す。
(1) 左半開区間での広義積分が収束するための必要十分条件
左半開区間(a,b]で連続だが、x=aが特異点となる関数f(x)を考える。
広義積分
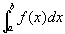
が収束するための必要十分条件は、
任意の正の実数εに対して、
a<s<t<a+δならば、
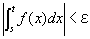
を成り立たせる、ある正数δが存在するということ。
すなわち、(∀ε>0)(∃δ>0) (∀s, t)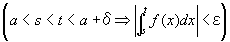 
※f(x)は左半開区間(a,b]で連続なのだから、閉区間[s,t] で連続、よって、f(x)は閉区間[s,t]でリーマン可積となるので(∵連続関数はリーマン可積分)、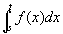
は、広義積分ではなく、普通の定積分。
[証明] 以下は、右半開区間での広義積分についてのコーシーの収束判定条件の証明を自力でカスタマイズしたもの。
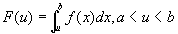…①
と定義する。
また、s<tとおく。…②
右極限の場合のコーシーの判定条件より、
u→a＋0のときF(u)が収束する(右極限をもつ)ための必要十分条件は、
任意の正数εに対して、
「0＜s－a＜δかつ0＜t－a＜δならば、|F(s)－F(t) |＜ε」
つまり「s, t∈( a, a＋δ)ならば、|F(s)－F(t) |＜ε」
を成り立たせる、ある正数δが存在するということ、
すなわち、(∀ε>0)(∃δ>0) (∀s, t) (s, t∈( a, a＋δ)⇒|F(s)－F(t) |＜ε) …※
※のF(u)を、①の定義にしたがって、積分に書き換えていく。
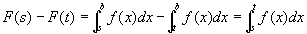（∵区間加法性と②より）
にも留意して。
すると、※は、以下になる。
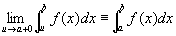
が収束するための必要十分条件は、
任意の正数εに対して、
「0＜s－a＜δかつ0＜t－a＜δ」つまり「s, t∈( a, a＋δ)」ならば、
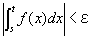
を成り立たせる、ある正数δが存在するということ、
すなわち、(∀ε>0)(∃δ>0) (∀s, t)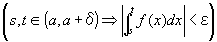
②を用いて、整理すると、
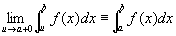
が収束するための必要十分条件は、
任意の正数εに対して、
a＜s＜t＜a＋δならば、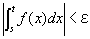 
を成り立たせる、ある正数δが存在するということ、
すなわち、(∀ε>0)(∃δ>0) (∀s, t)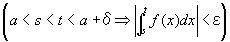 
(2) 右半開区間での広義積分が収束するための必要十分条件
右半開区間[a,b) で連続だが、x=bが特異点となる関数f(x)を考える。
広義積分
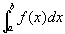
が収束するための必要十分条件は、
任意のの正の実数εに対して、
b－δ<s<t<bならば、
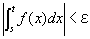
を成り立たせる、ある正数δが存在するということ。
すなわち、(∀ε>0)(∃δ>0) (∀s, t)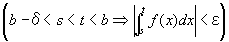
※f(x)は右半開区間[a,b)で連続なのだから、閉区間[s,t] で連続、よって、f(x)は閉区間[s,t]でリーマン可積となるので(∵連続関数はリーマン可積分)、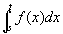は、広義積分ではなく、普通の定積分。
[証明] [小平『解析入門I』184;杉浦『解析入門I』292;住友『大学一年生の微積分学』124; ]
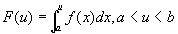…①
とおく。
また、s<tとおく。…②
左極限の場合のコーシーの判定条件より、
u→b－0のときF(u)が収束する(左極限をもつ)ための必要十分条件は、
任意の正数εに対して、
「－δ＜s－b＜0かつ－δ＜t－b＜0ならば、|F(t)－F(s) |＜ε」
つまり「s, t∈( b－δ, b )ならば、|F(t)－F(s) |＜ε」
を成り立たせる、ある正数δが存在するということ、
すなわち、(∀ε>0)(∃δ>0) (∀s, t) (s,t∈( b－δ, b )⇒|F(t)－F(s) |＜ε) …※
※のF(u)を、①の定義にしたがって、積分に書き換えていく。
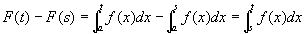（∵区間加法性と②より）
にも留意して。
すると、※は、以下になる。
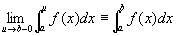
が収束するための必要十分条件は、
任意の正数εに対して、
「－δ＜s－b＜0かつ－δ＜t－b＜0」つまり「s, t∈( b－δ, b )」ならば、
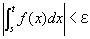
を成り立たせる、ある正数δが存在するということ、
すなわち、(∀ε>0)(∃δ>0) (∀s, t)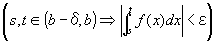
②を用いて、整理すると、
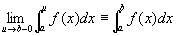
が収束するための必要十分条件は、
任意の正数εに対して、
b－δ＜s＜t＜bならば、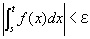 
を成り立たせる、ある正数δが存在するということ、
すなわち、(∀ε>0)(∃δ>0) (∀s, t)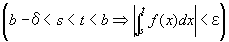 
(3) 無限区間での広義積分が収束するための必要十分条件
無限区間[a,∞) で連続な関数f(x)を考える。
広義積分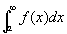 
が収束するための必要十分条件は、
任意の正の実数εに対して、
K<p<qならば、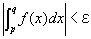
を成り立たせる、ある実数Kが存在するということ。
※f(x)は無限区間[a,∞)で連続なのだから、閉区間[p,q] で連続、よって、f(x)は閉区間[p,q]でリーマン可積となるので(∵連続関数はリーマン可積分)、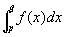
は、広義積分ではなく、普通の定積分。
[証明] [高木『解析概論』p.106-; Fischer, Intermediate Real Analysis,719; Lang,Undergraduate Analysis280.]
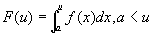…①
とおく。
コーシーの判定条件より、
u→∞のときF(u)が収束するための必要十分条件は、
任意の正数εに対して、
「 p,q＞K ならば、 ｜F(q)－F(p)｜＜ε 」
を成り立たせる、ある実数Kが存在する …※
ということ。
※のF(u)を、①の定義にしたがって、積分に書き換えていく。
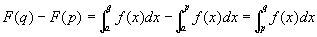（∵区間加法性）
にも留意して。
すると、※は、以下になる。
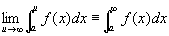
が収束するための必要十分条件は、
任意の正数εに対して、
「 p,q＞K ならば、 」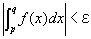
を成り立たせる、ある実数Kが存在する
ということ。
定理：広義積分が絶対収束するための十分条件のひとつ（ その1 ）
[杉浦『解析入門I』292.;吹田新保『理工系の微分積分学』117; 片山『微分積分学』120-121:証明なし。
住友『大学一年生の微積分学』122-126:懇切丁寧。]
以下、左半開区間/右半開区間/無限区間での広義積分に分けて、絶対収束の十分条件を示す。
(1) 左半開区間での広義積分が絶対収束するための十分条件のひとつ
左半開区間(a,b]で連続な関数f(x), g(x)を考える。
左半開区間(a,b]上どこでも、|f(x)|≦g(x)
かつ
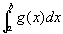
が収束する
ならば、
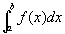
は絶対収束する。
証明：(2) 右半開区間での広義積分が絶対収束するための十分条件の証明を自力でカスタマイズしたもの
f(x), g(x)は、左半開区間(a,b]で連続…(仮定1)
左半開区間(a,b]上どこでも、0≦|f(x)|≦g(x) …(仮定2)
広義積分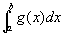
が収束する…(仮定3)
が成り立つと仮定する。
(仮定1)のもとでは、f(x), g(x)は、左半開区間(a,b]に含まれる任意の閉区間[a',b']上で連続、よって、f(x), g(x)は、任意の閉区間[a',b']⊂(a,b]でリーマン可積(∵連続関数はリーマン可積分)。…(仮定1')
(仮定1')と(仮定2)のもとでは、定積分の単調性〇1〇2が、|f(x)|, g(x)について成り立ち、
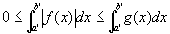…(仮定2')
(仮定3)は、コーシーの判定条件より、次のように言い換え可能である。
任意の正の実数εに対して、
a<s<t<a+δならば、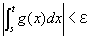 
を成り立たせる、ある正数δが存在するということ
すなわち、(∀ε>0)(∃δ>0) (∀s, t)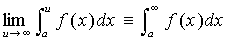 
…(仮定3' )
(仮定3')にでてくる閉区間[s,t]は、(a,b]に含まれる閉区間であるので、ここでも(仮定2')が成立し、
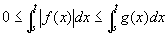
非負であることから、絶対値をかけても変わらず、
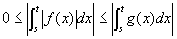
これを(仮定3' )に組み入れると、
任意の正の実数εに対して、
a<s<t<a+δならば、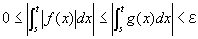 
を成り立たせる、ある正数δが存在するということ
すなわち、(∀ε>0)(∃δ>0) (∀s, t)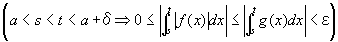
よって、(仮定1～3)が成り立つなら、
任意の正の実数εに対して、
a<s<t<a+δならば、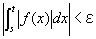 
を成り立たせる、ある正数δが存在する
すなわち、(∀ε>0)(∃δ>0) (∀s, t)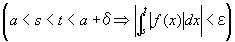 
が成り立ち、このとき、コーシーの判定条件より、広義積分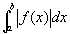
は収束するといってよい。
よって、(仮定1～3)が成り立つなら、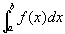は絶対収束する。
(2) 右半開区間での広義積分が絶対収束するための十分条件のひとつ
右半開区間[a,b) で連続な関数f(x), g(x)を考える。
右半開区間[a,b)上どこでも、|f(x)|≦g(x) かつ 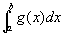が収束するならば、
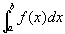は絶対収束する。
証明：[住友『大学一年生の微積分学』124-125; 杉浦『解析入門I』292.]
f(x), g(x)は、右半開区間[a,b) で連続…(仮定1)
右半開区間[a,b)上どこでも、0≦|f(x)|≦g(x) …(仮定2)
広義積分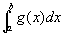が収束する…(仮定3)
が成り立つと仮定する。
(仮定1)のもとでは、f(x), g(x)は、右半開区間[a,b)に含まれる任意の閉区間[a',b']上で連続、よって、f(x), g(x)は、任意の閉区間[a',b']⊂[a,b)でリーマン可積(∵連続関数はリーマン可積分)。…(仮定1')
(仮定1')と(仮定2)のもとでは、定積分の単調性〇1〇2が、|f(x)|, g(x)について成り立ち、
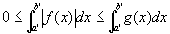…(仮定2')
(仮定3)は、コーシーの判定条件より、次のように言い換え可能である。
任意の正の実数εに対して、
b－δ<s<t<bならば、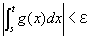
を成り立たせる、ある正数δが存在するということ
すなわち、(∀ε>0)(∃δ>0) (∀s, t)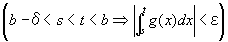 
…(仮定3' )
(仮定3')にでてくる閉区間[s,t]は、 [a,b)に含まれる閉区間であるので、ここでも(仮定2')が成立し、
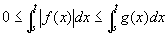
非負であることから、絶対値をかけても変わらず、
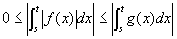
これを(仮定3' )に組み入れると、
任意の正の実数εに対して、
b－δ<s<t<bならば、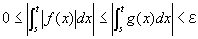
を成り立たせる、ある正数δが存在するということ
すなわち、(∀ε>0)(∃δ>0) (∀s, t)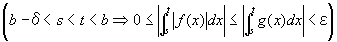 
よって、(仮定1～3)が成り立つなら、
任意の正の実数εに対して、
b－δ<s<t<bならば、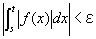
を成り立たせる、ある正数δが存在する
すなわち、(∀ε>0)(∃δ>0) (∀s, t)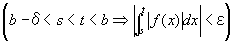 
が成り立ち、このとき、コーシーの判定条件より、広義積分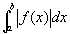は収束するといってよい。
よって、(仮定1～3)が成り立つなら、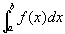は絶対収束する。
(3) 無限区間での広義積分が絶対収束ための十分条件
無限区間[a,∞) で連続な関数f(x), g(x)を考える。
無限区間[a,∞)上どこでも、|f(x)|≦g(x)
かつ
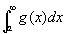
が収束する
ならば、
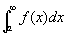
は絶対収束する。
証明：(2) 右半開区間での広義積分が絶対収束するための十分条件の証明を自力でカスタマイズしたもの
f(x), g(x)は、無限区間[a,∞) で連続…(仮定1)
無限区間[a,∞)上どこでも、0≦|f(x)|≦g(x) …(仮定2)
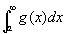が収束する…(仮定3)
が成り立つと仮定する。
(仮定1)のもとでは、f(x), g(x)は、[a,∞) に含まれる任意の閉区間[a',b']上で連続、よって、f(x), g(x)は、任意の閉区間[a',b']⊂[a,b)でリーマン可積(∵連続関数はリーマン可積分)。…(仮定1')
(仮定1')と(仮定2)のもとでは、定積分の単調性〇1〇2が、|f(x)|, g(x)について成り立ち、
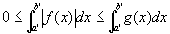…(仮定2')
(仮定3)は、コーシーの判定条件より、次のように言い換え可能である。
任意の正の実数εに対して、
K<p<q ならば、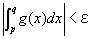 
を成り立たせる、ある実数Kが存在するということ
すなわち、(∀ε>0)(∃K>0) (∀p, q)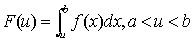 
…(仮定3' )
(仮定3')にでてくる閉区間[p,q]は、[a,∞) に含まれる閉区間であるので、ここでも(仮定2')が成立し、
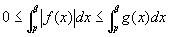
非負であることから、絶対値をかけても変わらず、
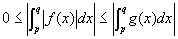
これを(仮定3' )に組み入れると、
任意の正の実数εに対して、
K<p<q ならば、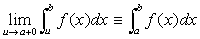 
を成り立たせる、ある実数Kが存在するということ
すなわち、(∀ε>0)(∃K>0) (∀p, q)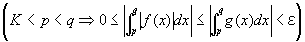 
よって、(仮定1～3)が成り立つなら、
任意の正の実数εに対して、
K<p<q ならば、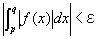 
を成り立たせる、ある実数Kが存在する
すなわち、(∀ε>0)(∃K>0) (∀p, q)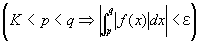 
が成り立ち、このとき、コーシーの判定条件より、広義積分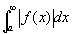
は収束するといってよい。
よって、(仮定1～3)が成り立つなら、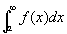は絶対収束する。
定理：広義積分が絶対収束するための十分条件のひとつ ( その2 )
[高木『解析概論』pp.106-107;小平『解析入門I』187-188:証明つき; 吹田新保『理工系の微分積分学』118:証明なし.
住友『大学一年生の微積分学』122-126:懇切丁寧。片山『微分積分学』120-123。]
意義：「|f(x)|をその広義積分が収束することが知られている標準的な関数と比較する」ことによって、
「f(x)の広義積分が絶対収束することを証明」できる。[小平『解析入門I』p.187]
応用例→ガンマ関数が収束することの証明、
(1) 左半開区間での広義積分が絶対収束するための十分条件のひとつ
左半開区間(a,b]で連続だが、x=aが特異点となる関数f(x)を考える。
「左半開区間(a,b]において、
(x-a)λ|f(x)|≦M を満たす0<λ<1なるλ、定数Mがそれぞれ一つでも存在するならば、」…(※)
すなわち、
「左半開区間(a,b]において、
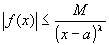
を満たす0<λ<1なるλ、定数Mがそれぞれ一つでも存在するならば、」 …(※※)
広義積分
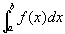
は絶対収束する。（ゆえに、収束する。）
[注] 条件(※)と(※※)は同じこと。
左半開区間(a,b]について考えている限り、常にa<xなので、(x-a)λ>0。
よって、(x-a)λ|f(x)|≦M の両辺を、(x-a)λで割っても不等号の向きはかわらない。
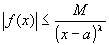
の両辺に、(x-a)λをかけても不等号の向きはかわらない。
[解釈1] (※)を、「左半開区間(a,b]において、0<λ<1なるλにたいして、(x-a)λ|f(x)|が 上に有界（でMという上界がある)ならば、」と表現できる。なお、左半開区間(a,b]においては常にa<xなので、(x-a)λ>0、また|f(x)|≧0より、そもそも、(x-a)λ|f(x)| は、下に有界。だから、「左半開区間(a,b]において、0<λ<1なるλにたいして、(x-a)λ|f(x)|が有界ならば、」といっても同じ。[高木『解析概論』pp.106-107;吹田新保『理工系の微分積分学』118.]
[解釈2] (※※)を「f(x)の広義積分が絶対収束することを証明するのに、|f(x)|をその広義積分が収束することが知られている標準的な関数と比較[小平『解析入門I』p.187]」していると解釈できる。
証明：[高木『解析概論』107。右半開区間についての小平『解析入門I』188;住友『大学一年生の微積分学』126も参照]
(方針) g(x)=M/(x-a)λとおくと、|f(x)|≦g(x) の成立がすでに仮定されているので、定理より、あと、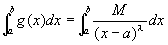
がつねに収束することを示しさえすれば、
「 (※※) ならば、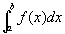は絶対収束する 」
を示したことになる。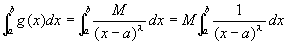
がつねに収束することを示すために、まず、
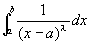の収束を示すところから手をつけていくことになる。
Step1: h(x)=1/(x-a)λの特徴を把握する
h(x)=1/(x-a)λ (0<λ<1) とおく。
※なお、h(x)は、λ' =1/λ(0<λ<1より、λ' >1)とおけば、
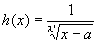
ともかけるし、
h(x) =(x-a)－λ ともかける。
まず、h(x)はx=aで特異点をとる(h(a)=1/0だから)。
また、h(x)は1/xλ=x－λ(0<λ<1) を 、座標平面上右方向にaだけ平行移動したグラフとなる。
1/xλ= x－λ(0<λ<1)は区間 (0 , ＋∞) で連続・単調減少、xλ→＋∞(x→＋0)、xλ→0(x→＋∞)だから、
これを、右方向にaだけ平行移動したh(x)は、
区間 (a , ＋∞) で連続・単調減少、xα→＋∞(x→a＋0)、xα→0(x→＋∞)となる。
Step2: h(x)の(a,b]での広義積分は収束する。
以上から、h(x)=1/(x-a)λ(0<λ<1)は、左半開区間(a,b]では連続だが、x=aで特異点をとる、とわかった。
よって、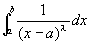とは、厳密には、
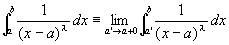
である。
広義積分についての微分積分学の基本定理によれば、
h(x)の不連続点を除いて― つまり (a,b]で ―、原始関数H(x)が存在し、かつ、h(x)の不連続点x=aでもH(x)が連続であるなら、広義積分はH(b)－H(a)に収束する。はたして、このような原始関数H(x)は存在するのだろうか。
0<λ<1とされており、λは1にならないので、ベキ関数の原始関数の公式を用いて、
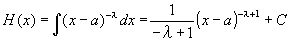
（合成関数であることが気になるなら、置換積分法をチェックせよ。）
h(x)の不連続点x=aでもH(x)は連続なのだろうか。
0<λ<1とされているから、0<－λ+1<1となるので、(x-a)－λ＋１は累乗根のかたちにはなるけれども、(x-a)が分母に来るということはなく、x=aでH(x)は右連続で、H(a)=Cが存在する。
よって、
h(x)の原始関数H(x)が存在し、かつ、h(x)の不連続点x=aを含む閉区間[a,b]でH(x)が連続となるので、
広義積分についての微分積分学の基本定理によって、広義積分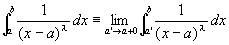は収束することが保証されたことになる。…(1)
Step3: g(x)=M/(x-a)λの(a,b]での広義積分は収束する。
g(x)=M/(x-a)λとおく(M :定数、0<λ<1)。
また、g(x)=M h(x)で、なおかつ、h(x)は、左半開区間(a,b]では連続だから、連続性の性質より、g(x)も、左半開区間(a,b]で連続となる。…(2)
g(x)＝M h(x)で、なおかつ、(1)より広義積分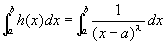
も収束するのだから、
広義積分の線形性より
広義積分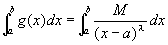
も収束する。…(3)
Step4: 結論。
定理より、
条件1.関数f(x), g(x)が左半開区間(a,b]で連続、
かつ、条件2. (a,b]上どこでも、|f(x)|≦g(x)、
かつ、条件3. 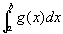が収束する
ならば、
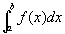は絶対収束する。
g(x)=M/(x-a)λ (M :定数、0<λ<1)ならば、つねに、(2)が成立して条件1.が満たされ、(3)が成立して条件3.が満たされる。よって、g(x)=M/(x-a)λ (M :定数、0<λ<1) かつ、条件2: |f(x)|≦g(x)= M/(x-a)λならば、条件１～3の全てが満たされ、 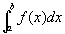は絶対収束する。
(2) 右半開区間での広義積分が絶対収束するための十分条件のひとつ
右半開区間[a,b) で連続だが、x=bが特異点となる関数f(x)を考える。
「右半開区間[a,b)において、
(b-x)λ|f(x)|≦M を満たす
0<λ<1なるλ、定数Mがそれぞれ一つでも存在するならば、」 …(※)
すなわち、
「右半開区間[a,b)において、
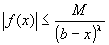
を満たす0<λ<1なるλ、定数Mがそれぞれ一つでも存在するならば、」…(※※)
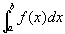
は絶対収束する。（ゆえに、収束する。）[小平『解析入門I』pp.187-188]
[注] 条件(※)と(※※)は同じこと。
右半開区間[a,b)について考えている限り、常にx < bなので、(b-x)λ>0。
よって、(b-x)λ|f(x)|≦M の両辺を、(b-x)λで割っても不等号の向きはかわらない。
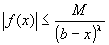
の両辺に、(b-x)λをかけても不等号の向きはかわらない。
[解釈1] (※)を、「右半開区間[a,b)において、0<λ<1なるλにたいして、 (b-x)λ|f(x)|が 上に有界（でMという上界がある)ならば、」と表現できる。なお、右半開区間[a,b)においては常にx < bなので、(b-x)λ>0、また|f(x)|≧0より、そもそも、(b-x)λ|f(x)| は、下に有界。だから、「右半開区間[a,b)において、0<λ<1なるλにたいして、 (b-x)λ|f(x)|が有界ならば、」といっても同じ。[高木『解析概論』pp.106-107;吹田新保『理工系の微分積分学』118.]
[解釈2] (※※)を「f(x)の広義積分が絶対収束することを証明するのに、|f(x)|をその広義積分が収束することが知られている標準的な関数と比較[小平『解析入門I』p.187]」していると解釈できる。
証明: [小平『解析入門I』188;住友『大学一年生の微積分学』126。左半開区間についての高木『解析概論』107-も参照]
(方針) g(x)=M/(b-x)λとおくと、|f(x)|≦g(x) の成立がすでに仮定されているので、定理より、あと、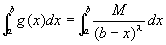
がつねに収束することを示しさえすれば、
「 (※※) ならば、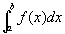は絶対収束する 」
を示したことになる。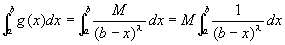
ががつねに収束することを示すために、まず、
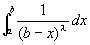の収束を示すところから手をつけていくことになる。
Step1: h(x)=1/(x-a)λの特徴を把握する
h(x)=1/(b- x)λ (0<λ<1) とおく。
※なお、h(x)は、λ' =1/λ(0<λ<1より、λ' >1)とおけば、
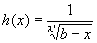
ともかけるし、
h(x) =(b-x)－λ={-(x -b)}－λ ともかける。
まず、h(x)はx=bで特異点をとる(h(b)=1/0だから)。
また、h(x)のグラフは、1/xλ=x－λ(0<λ<1)とy軸について線対称な (－x)－λ(0<λ<1)を、座標平面上右方向にbだけ平行移動したグラフとなる。
1/xλ= x－λ(0<λ<1)は区間 (0 , ＋∞) で連続・単調減少、xλ→＋∞(x→＋0)、xλ→0(x→＋∞)だから、
これを、左右ひっくり返して右方向にbだけ平行移動したh(x)は、
区間 (－∞, b) で連続・単調増加、xλ→＋∞(x→b－0)、xλ→0(x→－∞)となる。
Step2: h(x)の [a,b)での広義積分は収束する。
以上から、h(x)=1/(x-a)λ(0<λ<1)は、右半開区間[a,b)では連続だが、x=bで特異点をとる、とわかった。
よって、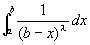とは、厳密には、
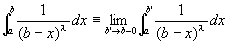
である。
広義積分についての微分積分学の基本定理によれば、
h(x)の不連続点を除いて― つまり [a,b)で ―、原始関数H(x)が存在し、かつ、h(x)の不連続点x=bでもH(x)が連続であるなら、広義積分はH(b)－H(a)に収束する。はたして、このような原始関数H(x)は存在するのだろうか。
0<λ<1とされており、λは1にならないので、(ax+b)n の原始関数を求める公式(n≠－1)を用いて、
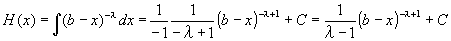
h(x)の不連続点x=bでもH(x)は連続なのだろうか。
0<λ<1とされているから、0<－λ+1<1となるので、(b-x)－λ＋１は累乗根のかたちにはなるけれども、(b-x)が分母に来るということはなく、x=bでH(x)は左連続で、H(b)=Cが存在する。
よって、
h(x)の原始関数H(x)が存在し、かつ、h(x)の不連続点x=bを含む閉区間[a,b]でH(x)が連続となるので、
広義積分についての微分積分学の基本定理によって、広義積分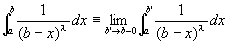は収束することが保証されたことになる。…(1)
Step3: g(x)=M/(b-x)λの[a,b)でのでの広義積分は収束する。
g(x)=M/(b-x)λとおく(M :定数、0<λ<1)。
また、g(x)=M h(x)で、なおかつ、h(x)は、右半開区間[a,b)では連続だから、連続性の性質より、g(x)も、右半開区間[a,b)で連続となる。…(2)
g(x)＝M h(x)で、なおかつ、(1)より広義積分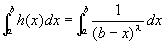
も収束するのだから、
広義積分の線形性より
広義積分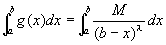
も収束する。…(3)
Step4: 結論。
定理より、
条件1.関数f(x), g(x)が右半開区間[a,b)で連続、
かつ、条件2. [a,b)上どこでも、|f(x)|≦g(x)、
かつ、条件3. 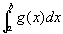が収束する
ならば、
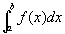は絶対収束する。
g(x)=M/(b-x)λ (M :定数、0<λ<1)ならば、つねに、(2)が成立して条件1.が満たされ、(3)が成立して条件3.が満たされる。よって、g(x)=M/(b-x)λ (M :定数、0<λ<1) かつ、条件2: |f(x)|≦g(x)= M/(b-x)λならば、条件１～3の全てが満たされ、 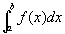は絶対収束する。
(3) 無限区間[a,∞)における広義積分が絶対収束するための十分条件のひとつ
[高木『解析概論』pp.106-107; 小平『解析入門I』pp.187-188.:証明つき; 吹田新保『理工系の微分積分学』p.118:証明なし.
住友『大学一年生の微積分学』126-128:懇切丁寧。片山『微分積分学』120-123。]
応用例→ガンマ関数、
意義：「|f(x)|をその広義積分が収束することが知られている標準的な関数と比較する」ことによって、
「f(x)の広義積分が絶対収束することを証明」できる。[小平『解析入門I』p.187]
無限区間[a,∞) , a > 0, で連続な関数f(x)を考える。
「無限区間[a,∞) , a > 0において、
xλ|f(x)|≦M
を満たす1<λなるλ、定数Mがそれぞれ一つでも存在するならば、」 …(※)
すなわち、
「無限区間[a,∞) , a > 0において、
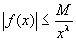
を満たす1<λなるλ、定数Mがそれぞれ一つでも存在するならば、」 …(※※)
広義積分
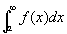
は絶対収束する。（ゆえに、収束する。）
[注] 条件(※)と(※※)は同じこと。
無限区間[a,∞) , a > 0,について考えている限り、常に0<a<xなので、xλ>0。
よって、xλ|f(x)|≦M の両辺を、xλで割っても不等号の向きはかわらない。
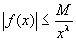
の両辺に、xλをかけても不等号の向きはかわらない。
[解釈1] [高木『解析概論』pp.106-107;吹田新保『理工系の微分積分学』118.]
(※)を、
「無限区間[a,∞) , a > 0,において、1<λなるλにたいして、
xλ|f(x)|が 上に有界（でMという上界がある)ならば、」
と表現できる。
なお、無限区間[a,∞) , a > 0,においては常に0<a<xなので、xλ>0、また|f(x)|≧0より、
そもそも、xλ|f(x)| は、下に有界。
だから、「無限区間[a,∞) , a > 0,において、1<λなるλにたいして、
xλ|f(x)|が有界ならば、」
といっても同じ。
[解釈2]
(※※)を
「f(x)の広義積分が絶対収束することを証明するのに、
|f(x)|をその広義積分が収束することが知られている標準的な関数と比較[小平『解析入門I』p.187]」
していると解釈できる。
[証明][高木『解析概論』pp.106-107]
(方針) g(x)=M/xλとおくと、|f(x)|≦g(x) の成立がすでに仮定されているので、定理より、あと、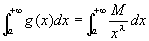
がつねに収束することを示しさえすれば、
「 (※※) ならば、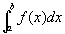は絶対収束する 」
を示したことになる。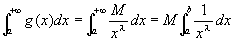
がつねに収束することを示すために、まず、
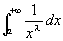の収束を示すところから手をつけていくことになる。
Step1: h(x)=1/xλの特徴を把握する
h(x) = 1/xλ = x－λ (1<λ) とおく。
h(x)=1/xλ= x－λ(1<λ)は区間 (0 , ＋∞) で連続・単調減少、x－λ→＋∞(x→＋0)、x－λ→0(x→＋∞)。
よって、h(x)=1/xλ= x－λ(1<λ)は [a,∞), a > 0 で連続でこの区間上に特異点をもたない。…(1)
Step2: h(x)の[a,b]での定積分を求める。
まず、閉区間[a,b] , a > 0における、h(x)の定積分を求める。
・h(x) =1/xλ= x－λ(1<λ)の原始関数は、λは1にならないので、ベキ関数の原始関数の公式を用いて、
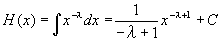
・(1)からh(x) =1/xλ= x－λ(1<λ)は[a,b]で連続だから、h(x)の[a,b]での定積分の計算に、定積分についての微分積分学の基本定理が使える。
よって、
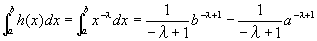
Step3: h(x)の[a,∞)での広義積分は収束する。
1<λより、－λ＋1＜0なので、α＜0のときのf(x)=xαに共通な性格より、b→＋∞とすると、b－λ＋1→0。
よって、
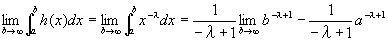
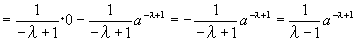
つまり、h(x)の[a,∞)での広義積分は、a－λ＋1/(λ－1)に収束する。
Step3: g(x)=M/xλの[a,∞)での広義積分は収束する。
g(x)=M/xλとおく(M :定数、λ>1)。
g(x)=M h(x)で、なおかつ、(1)よりh(x)は [a,∞)で連続だから、連続性の性質より、g(x)も、[a,∞)で連続となる。…(2)
g(x)＝M h(x)で、なおかつh(x)の[a,∞)での広義積分は収束するのだから、
広義積分の線形性より
M h(x)の[a,∞)での広義積分も収束する…(3)
Step4: 結論。
定理より、
条件1.関数f(x), g(x)が無限区間[a,∞) で連続、
かつ、条件2. [a,∞)上どこでも、|f(x)|≦g(x)、
かつ、条件3. 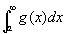が収束する
ならば、
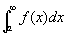は絶対収束する。
g(x)=M/xλ (M :定数、λ＞1)ならば、つねに、(2)が成立して条件1.が満たされ、(3)が成立して条件3.が満たされる。よって、g(x)=M/xλ (M :定数、λ＞1)かつ、条件2: |f(x)|≦g(x)=M/xλ (M :定数、λ＞1)ならば、条件１～3の全てが満たされ、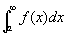 は絶対収束する。
有限区間における広義積分が絶対収束するための十分条件のひとつ
[青本『微分と積分1』p.139.]
意義：「|f(x)|をその広義積分が収束することが知られている標準的な関数と比較する」ことによって、
「f(x)の広義積分が絶対収束することを証明」できる。[小平『解析入門I』p.187]
応用例→ガンマ関数、ベータ関数
左半開区間(a,b]において、f(x)が区分的に連続で、
0<λなるλ、正の定数Cにたいして、
| f(x)|≦C(x-a)λ－1
ならば、
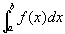
は絶対収束する。（ゆえに、収束する。）
また、右半開区間[a,b)でf(x)が区分的に連続で、
0<λなるλ、正の定数Cにたいして、
| f(x)|≦C(b - x)λ－1
ならば、
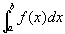
は絶対収束する。（ゆえに、収束する。）[青本『微分と積分1』p.139.]
※コーシーの判定法から。
定理：無限区間における広義積分が絶対収束するための十分条件のひとつ
[青本『微分と積分1』p.140.]
意義：「|f(x)|をその広義積分が収束することが知られている標準的な関数と比較する」ことによって、
「f(x)の広義積分が絶対収束することを証明」できる。[小平『解析入門I』p.187]
応用例→ガンマ関数、ベータ関数
2. 無限区間[a,+∞)、ないし、 (－∞,b]においてf(x) が区分的に連続で、
1<λなるλ、定数Cにたいして、
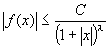
となるならば、
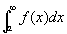ないし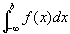 
は収束する。 [青本『微分と積分1』p.140.]
（reference）
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年、pp.184-188。
高木貞治『解析概論改訂第3版』岩波書店、1983年、pp.105-108;
杉浦光夫『解析入門I』岩波書店、1980年、p.292.
青本和彦『岩波講座現代数学への入門：微分と積分1』 岩波書店、1995年、pp.139-141。
吹田・新保『理工系の微分積分学』学術図書出版社、1987年、pp.117-9。
住友洸『大学一年生の微積分学』現代数学社、1987年、pp.122-128。
片山孝次『微分積分学』(現代数学レクチャーズB-8)、培風館、1980年、pp. 118-123。
Fischer,Emanuel.Intermediate Real Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Heidelberg Berlin,1983,pp. 715-726.
Lang,Serge.Undergraduate Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1983,pp.280-286.