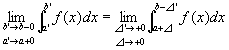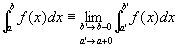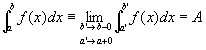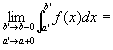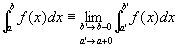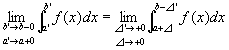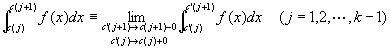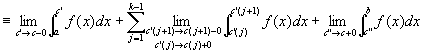1変数非有界関数unbounded function の広義積分improper integralの定義
【トピック一覧】
・定義:特異点・不連続点
・定義:閉区間の片方の端点が特異点である場合の広義積分可能・広義積分/閉区間の両端が特異点である場合の広義積分可能・広義積分
・定義:閉区間の中の一点が特異点である場合の広義積分可能・広義積分/閉区間の中に有限個の特異点がある場合の広義積分可能・広義積分
・主値積分・Cauthyの主値
【関連ページ:1変数関数の広義積分について】
前:無限区間における広義積分定義
次:性質・向き付き広義積分・積分関数・解析学の基本定理・収束条件・ガンマ関数ベータ関数
cf. 1変数関数の定積分、2変数関数の広義積分、n変数関数の広義積分
→総目次
定義:特異点singular point・不連続点
[高木『解析概論』103; 吹田新保『理工系の微分積分学』114; 高橋『経済学とファイナンスのための数学』90]
被積分関数f(x)が、その近傍において、有界でない(発散する)点。すなわち、
 [高木『解析概論』103:脚注]
[高木『解析概論』103:脚注]
小平『解析入門I』p.175や和達『微分積分』p.100などでは、「特異点」なる語は使用せず、「不連続点」なる語を用いている。話を簡潔に進めるべく、連続関数のみに絞ってリーマン積分を論じているためだと思われる(実際には、連続でない関数についてもリーマン可積となることもある。)。
例:
|
・x=0 における f (x) = |
|
|
1
|
| [和達『微分積分』p.100]
|
|
|
|
x
|
|
・x=0 における f(x) =
|
|
[高木『解析概論』103;]
|
定義:閉区間の片方の端点が特異点である場合の、
広義積分可能improper integrable・広義積分improper integral
[高木『解析概論』103; 吹田新保『理工系の微分積分学』114 ; 杉浦『解析入門I』290-291;LangUndergraduateAnalysis,276;Fischer.IntermediateRealAnalysis,pp.711-712;RossA.Elementary Analysis,221;高橋『経済学とファイナンスのための数学』90; 岡田章『経済学・経営学のための数学』241-242.]
「積分の定義の拡張において、我々は積分関数の連続性と区間に関する加法性とを指導原理とする。それは妥当であろう。(高木『解析概論』103)」「実際、これらの性質(広義積分における積分関数の連続性・広義積分における区間加法性)を目標として広義積分が定義されたのであった。(高木『解析概論』104)」
[左の端点が特異点である場合]
(前提)
閉区間[a,b]において、その境界点aだけが特異点で、
それを除いた区間、
すなわち、任意のa' ( a<a'<b )に対して[a',b]
において、f(x)は有界かつリーマン可積とする。
(定義)
右極限値
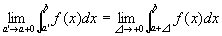
が存在するならば、
f(x)は左半開区間(a,b]で、「広義積分可能improper integrableである」「広義積分は収束する」といい、
この右極限値で、広義積分improper integral
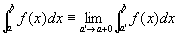
を定義する。
(右極限値の定義に遡って、この定義をε-δ論法で書き下すと…)
左半開区間(a,b]における広義積分の値がAである、すなわち、
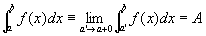
とは、
任意の正数εに対して、
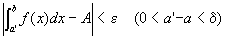
つまり、
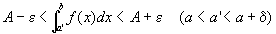
を成り立たせる、ある正の実数δが存在する
ことである。
なお、前提とここまでの説明でわかるように、
ここで問題にしている
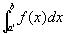
は、普通のリーマン定積分であることに注意。
[類似例:小平『解析入門I』176.]
[右の端点が特異点である場合]
(前提)
閉区間[a,b]において、その境界点bだけが特異点で、
それを除いた区間、
すなわち、任意のb' ( a<b'<b )に対して[a,b']
において、f(x)は有界かつリーマン可積とする。
(定義)
左極限値
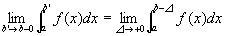
が存在するならば、
f(x)は右半開区間[a,b)で、「広義積分可能improper integrableである」「広義積分は収束する」といい、
この左極限値で、広義積分improper integral
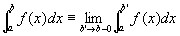
を定義する。
(左極限値の定義に遡って、この定義をε-δ論法で書き下すと…)
右半開区間[a,b)における広義積分の値がAである、すなわち、
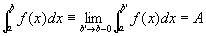
とは、
任意の正数εに対して、
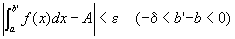
つまり、
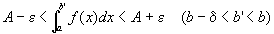
を成り立たせる、ある正の実数δが存在する
ことである。
なお、前提とここまでの説明でわかるように、
ここで問題にしている
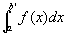
は、普通のリーマン定積分であることに注意。
[類似例:小平『解析入門I』176.]
定義:閉区間の両端が特異点である場合の、
広義積分可能improper integrable・広義積分improper integral
[小平『解析入門I』176;高木『解析概論』104;高橋『経済学とファイナンスのための数学』91; 杉浦『解析入門I』291; LangUndergraduate Analysis,277;Fischer .Intermediate Real Analysis, 714. ; Ross A.Elementary Analysis,221;]
(前提)
閉区間[a,b]において、その境界点a,bだけが特異点で、
それを除いた区間、
すなわち、任意のa',b' (a< a'<b'<b )に対して[a',b']
において、f(x)は有界かつリーマン可積とする。
(定義1)[小平『解析入門I』176;高木『解析概論』104;高橋『経済学とファイナンスのための数学』91;]
極限値
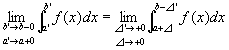
が存在するならば、
f(x)は開区間(a,b)で、「広義積分可能improper integrableである」「広義積分は収束する」といい、
この極限値で、広義積分improper integral
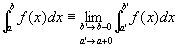
を定義する。
(ε-δ論法による厳密な定義) [小平『解析入門I』176.]
開区間(a,b)における広義積分の値がAである、すなわち、
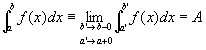
とは、
任意の正数εに対して、
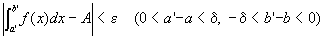
つまり、
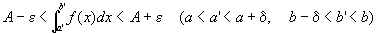
を成り立たせる、ある正の実数δが存在する
ことである。
なお、前提とここまでの説明でわかるように、
ここで問題にしている
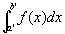
は、普通のリーマン定積分であることに注意。
(定義2)
[小平『解析入門I』176; 杉浦『解析入門I』291;LangUndergraduate Analysis,277;Fischer .Intermediate Real Analysis, 714. ; Ross A.Elementary Analysis,221;]
a < c < bを満たす任意の一点をcとする。
広義積分
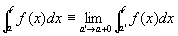
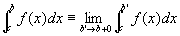
がともに収束するならば広義積分improper integral
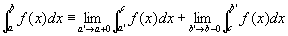
を定義する。
※これはcのとり方によらず一定となる。なぜか、については、LangUndergraduate Analysis,277を参照せよ。
※二つの極限=広義積分を別個にとることに注意。Cf.コーシーの主値。
(定義1と定義2は同じ)[小平『解析入門I』176; 杉浦『解析入門I』291.]
要点: 広義積分も、定義にまで遡ると、普通のリーマン定積分であるから、
普通のリーマン定積分の区間加法性を適用できる。
Step1: 定義1・定義2に共通の前提
閉区間[a,b]において、その境界点a,bだけが特異点である。
だから、それを除いた区間、
すなわち、任意のa',b' (a< a'<b'<b )からつくった閉区間[a',b']
において、f(x)は有界かつリーマン可積である。…①
Step2: 普通のリーマン定積分の区間加法性を適用
ゆえに、
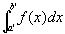
は、普通のリーマン定積分なのだから、普通のリーマン定積分の区間加法性が成り立つ。
よって、a'<c<b'を満たすcを一つ決めれば、
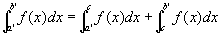 …③
…③
Step3:極限をとる
ここで、b'→b-0、a'→ a +0としても、
b'=b、a'=aとなるところまで行かないから、
やはり、
①より、[a',b']において、f(x)は有界かつリーマン可積であり、
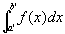
は、普通のリーマン定積分となり、普通のリーマン定積分の区間加法性が成り立つ。
よって、b'→b - 0、a'→ a +0としても、③は成り立つ。
つまり、
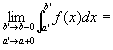
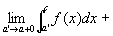
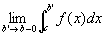
結論:以上から、
定義式1
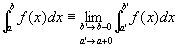
の右辺と、
定義式2
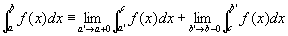
の右辺は一致することになり、どちらの定義でもかわらないことがわかる。
Question:定義1における
「極限値
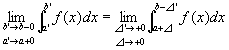
が存在する」
と、
定義2における
「広義積分
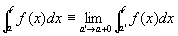
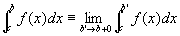
がともに収束する」
が同値であるという証明は?
定義:閉区間の中の一点が特異点である場合の、
広義積分可能improper integrable・広義積分improper integral
[高木『解析概論』104;吹田新保『理工系の微分積分学』114; Fischer .Intermediate Real Analysis, 714-5.]
高橋『経済学とファイナンスのための数学』91; ; 杉浦『解析入門I』290-291]
閉区間[a,b]の内点のうちの一点c ( すなわち、a< c <b)だけが特異点であり、
一点cを除いてできる二つの区間、
すなわち、任意のc', c'' (a< c'<c<c''<b )に対して[a,c'][c'',b]
において、f(x)は有界かつリーマン可積とする。
広義積分
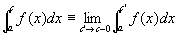
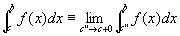
がともに存在するならば
f(x)は[a,b]で「広義積分可能improper integrableである」「広義積分は収束する」といい、
この二つの極限値を用いて、広義積分improper integral
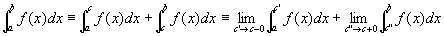
を定義する。
(上式最右辺でc'とc''とわざわざ別の変数でおいて極限を考えていることに注意。
これを共通のc'で極限をとると、コーシーの主値という別の概念になる。)
定義:閉区間の中に有限個の特異点がある場合の、
広義積分可能improper integrable・広義積分improper integral
[高木『解析概論』104;吹田新保『理工系の微分積分学』114; 杉浦『解析入門I』290-291;
高橋『経済学とファイナンスのための数学』91; 岡田章『経済学・経営学のための数学』242.]
閉区間[a,b]の内点のなかに、k個の特異点c(1), c(2), …,c(k) ( すなわち、a< c(1)< c(2)< …< c(k) <b)がある場合、
広義積分
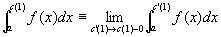
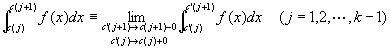
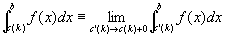
が全て収束する限りにおいて、
f(x)は[a,b]で「広義積分可能improper integrableである」「広義積分は収束する」といい、
これらのの極限値を用いて、広義積分improper integral
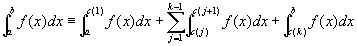
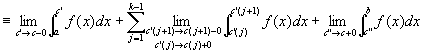
を定義する。
定義:主値積分・Cauthyの主値Cauthy principal value
下記文献参照。
・高木『解析概論』105;
・吹田新保『理工系の微分積分学』116;
・Fischer Intermediate Real Analysis, 715.
・『岩波数学辞典(第三版)』202項積分法: D.広義の積分(p.522);
・和達『微分積分』101.]
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、202項積分法(pp.520-525)。
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.113-7.
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.90-93.
和達三樹『理工系の数学入門コース1:微分積分』岩波書店、1988年、pp.98-103.
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年 pp.175-177閉区間で有限個の不連続点を持つばあい。
杉浦光夫『解析入門』東京大学出版会、1980年、pp.290-295:一変数関数の広義積分。
高木貞治『解析概論:改訂第3版』岩波書店、1983年、pp. 103-110.
青本和彦『岩波講座現代数学への入門:微分と積分1』岩波書店、1995年、138-142。
矢野健太郎・田代嘉宏『社会科学者のための基礎数学 改訂版』裳華房、pp.117-8.
岡田章『経済学・経営学のための数学』東洋経済新報社、2001年、pp.241-243。
Fischer,Emanuel.Intermediate Real Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Heidelberg Berlin,1983,pp.710-712.
Ross,Kenneth A.Elementary Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin Heidelberg Tokyo,1980,pp. 221.
Lang,Serge.Undergraduate Analysis
(Undergraduate Texts in Mathematics),Springer-Verlag New York Berlin
Heidelberg Tokyo,1983.=AnalysisI,Addison-Wesley,1968,pp. 276.