無限区間infinite intergalにおける広義積分improper integral の定義
【トピック一覧】
・定義:[a,∞)で広義積分可能 / (−∞, a]で広義積分可能 / (−∞, ∞)で広義積分可能
【関連ページ:1変数関数の広義積分について】
1変数関数の広義積分について:
前:有限区間における非有界関数の広義積分の定義
次:性質・向き付き広義積分・積分関数・解析学の基本定理・収束条件・ガンマ関数ベータ関数
cf. 1変数関数の定積分、2変数関数の広義積分、n変数関数の広義積分
→参考文献一覧・総目次
定義:[a,∞)で広義積分可能improper integrable
[高木『解析概論』104;吹田新保『理工系の微分積分学』114-5;高橋『経済学とファイナンスのための数学』91; 岡田章『経済学・経営学のための数学』242-3;]
f (x) は無限区間[a,∞)で定義されていて、a<a'を満たす任意のa' に対して、
次の定積分ないし広義積分が可能であるとする。
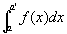
このとき、
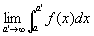
が有限な極限値に収束するならば、
f (x)は無限区間[a,∞)で「広義積分可能である」「広義積分は収束する」といい、
この極限値で、広義積分
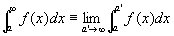
を定義する。
定義:(−∞, a]で広義積分可能improper integrable
[高木『解
析概論』104;吹田新保『理
工系の微分積分学』114-5; 高橋『経
済学とファイナンスのための数学』91]
f (x) は無限区間[a,∞)で定義されていて、a<a'を満たす任意のa' に対して、
次の定積分ないし広義積分が可能であるとする。
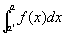
このとき、
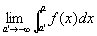
が有限な極限値に収束するならば、
f (x) は無限区間(−∞, a]で「広義積分可能である」「広義積分は収束する」といい、
この極限値で、広義積分
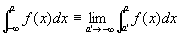
を定義する。
定義:(−∞, ∞)で広義積分可能improper integrable
[高木『解析概論』104;吹田新保『理工系の微分積分学』114-5; 高橋『経済学とファイナンスのための数学』91]
f (x)は無限区間(−∞, ∞)で定義されていて、
次の二つの広義積分がともに可能であるとする。
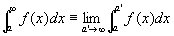
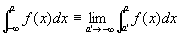
このとき、f (x) は無限区間(−∞, ∞)で「広義積分可能である」「広義積分は収束する」といい、
この二つの広義積分=極限値の和で、広義積分
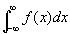
を定義する。すなわち、
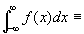
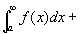
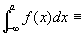
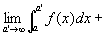
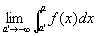
(reference)
日本数学会編集『岩波数学辞典(第三版)』 岩波書店、1985年、202項積分法(pp.520-525)→リーマン積分、204項積分論(pp.530-533)→ルベーク積分。
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.113-7.
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.90-93.
和達三樹『理工系の数学入門コース1:微分積分』岩波書店、1988年、pp.98-103.
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年 pp.175-191。あらかじめ閉区間上の連続関数に限定して議論を進めている。
杉浦光夫『解析入門』岩波書店、1980年、pp.290-295:一変数関数の広義積分。
高木貞治『解析概論 改訂第三版』岩波書店、1983年、pp. 103-110.
青本和彦『岩波講座現代数学への入門:微分と積分1』岩波書店、1995年、138-142。
矢野健太郎・田代嘉宏『社会科学者のための基礎数学 改訂版』裳華房、pp.106-9.
岡田章『経済学・経営学のための数学』東洋経済新報社、2001年、pp.241-243。
Fischer,Emanuel.Intermediate Real Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Heidelberg Berlin,1983,pp.710-712.