定義：分割 partition、分点、幅mesh
閉区間I[a,b]を、a=x0<x1<x2<…<xn=bを分点としたn個の小区間(ただし、すべて閉区間とする)に分けること、
すなわち、
Iを、I1=[a, x1], I2=[x1,x2],…,In=[xn-1,b] (a=x0<x1<x2<…<xn=b) に分けることを、
Iの分割(partitionあるいはdivision into subintervals)といい、記号⊿で表す。
各小区間の長さ⊿xk= xk－ xk－1 (k=1,2,…,n) の最大値、
すなわち、|⊿|=max⊿ xk
を、分割⊿の幅(mesh)と呼ぶ。
【文献】
・杉浦『解析入門I』205-207;
・吹田新保『理工系の微分積分学』102;
・神谷浦井『経済学のための数学入門』328-9.
・『岩波数学辞典（第三版）』202項積分法
定義：リーマン和 Riemann sum
→cf.リーマン・スチルチェス和。2変数関数のリーマン和。
f(x) を閉区間I [a,b]上の有界な関数とする。
閉区間Iの分割⊿によってできた小区間Ik (k=1,2,…,n)の各々から、
代表点ζkをとり、以下のように、積: f (ζk)・⊿ xk を k=1からnまで足し合せる。
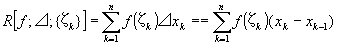
これを、⊿、{ζk }に関するfのリーマン和という。
※分割⊿、代表点ζkのとりかたは、いろいろであるから、リーマン和は、分割⊿、代表点ζkのとりかたに応じて、値を変えうる。リーマン和は、分割⊿、代表点ζkのある種の関数となっている。分割を細かくしていったときに、この関数が収束するかどうかという問題が、下記の積分可能の可否の問題に他ならない。
【文献】
・杉浦『解析入門I』205-207;
・吹田新保『理工系の微分積分学』102;
・神谷浦井『経済学のための数学入門』328-9;
・『岩波数学辞典（第三版）』202項積分法
定義：リーマン積分可能（可積） Riemann integrable
定義：定積分 definite integral
[杉浦『解析入門I』205-207; 吹田新保『理工系の微分積分学』102; 神谷浦井『経済学のための数学入門』330.; 『岩波数学辞典（第三版）』202項積分法]
f(x)を閉区間I[a,b]上の有界な関数とする。
閉区間Iの分割⊿を限りなく細かくしていくと、
分割⊿の取り方、それによってできた小区間Ik (k=1,2,…,n)の代表点ζkの取り方によらず、
⊿、{ζk }に関するfのリーマン和 R[ f ;⊿;{ζk } ]が値J に収束するとき、
※正確を期して書けば、
任意の（どんな）正の実数εに対して（でも）、
「 0＜|⊿|＜δ ならば
任意の(分点の取りかたで作れる)分割⊿、任意の代表点の取り方{ζk }に対して、
| R [ f ;⊿;{ζk}]－J|＜ε
を成り立たせる、ある正の実数δが存在する」とき、
※これを、記号で表すと、R [ f ;⊿;{ζk}] → J（|⊿|→0）
ないし、
、
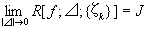f は閉区間I上で「(リーマン)積分可能」「(リーマン)可積分」である、という。
また、このとき、
値Jを「fのI上の定積分definite integral」「(リーマン)積分」などといい、
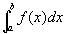
で表す。
また、f(x)を「被積分関数integrand」と呼び、定積分を求めることを「積分するintegrate」という。
→向きのついた定積分。
→Cf. リーマン・スチルチェス積分。
II. 積分可能性判定条件
リーマン和、そして、リーマン積分可能性は、その定義上、1. 分割⊿の取り方と、2.小区間Ik (k=1,2,…,n)の代表点ζkの取り方の両方に依存し、面倒である。2. 小区間の代表点ζkの取り方を用いずに、1. 分割⊿の取り方のみから、リーマン積分可能性を考えられないだろうか。そんな意図から展開されるのが、以下の議論。[杉浦『解析入門I』212]
定義：過剰和・不足和
・Iを閉区間[a,b]、f(x)をI上の有界な関数とする。
閉区間Iの分割⊿によって生じた各小区間Ik (k=1,2,…,n)でのfの下限をmk、上限をMkとおく。
すなわち、
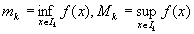
・各小区間Ik (k=1,2,…,n)の長さ⊿xkと、そこでのfの下限mkとの積を、
全ての区間について足し合わせたものを
不足和と呼び、s[⊿]で表す。すなわち、
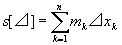
・各小区間Ik (k=1,2,…,n)の長さ⊿xkと、そこでのfの上限Mkとの積を、
全ての区間について足し合わせたものを
過剰和と呼び、S[⊿]で表す。すなわち、
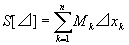
・不足和・過剰和は、リーマン和との間に以下の関係が成り立つ。
s[⊿]≦R [ f ;⊿;{ζk}]≦S[⊿]
（どのように小区間の代表点{ζk}をとっても、これは成立する）
【文献】
・杉浦『解析入門I』212.
・吹田新保『理工系の微分積分学』103.
定義：振動量・振幅 oscillation
[杉浦『解析入門I』212; 吹田新保『理工系の微分積分学』105.]
Iを閉区間[a,b]、f(x)をI上の有界な関数とする。
Iにおけるfの上限と下限との差を、f(x)のIにおける振幅といい、a ( f , I )で表す。
すなわち、
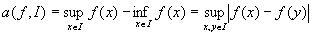
また、Iの分割⊿によって生じた各小区間Ik (k=1,2,…,n)でのfの上限と下限との差を
f(x)のIkにおける振幅・振動量などといい、ωk 、ω (Ik ; f )、a ( f, Ik )などと表す。
すなわち、
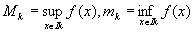
とおくと、
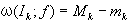
あるいは、
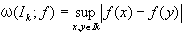
f(x)のIkにおける振動量は、不足和・過剰和との間に以下の関係が成り立つ
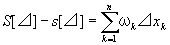
なぜなら、
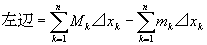
=(M1⊿x1＋M2⊿x2＋…＋Mn⊿xn)－(m1⊿x1＋m2⊿x2＋…＋mn⊿xn)
=(M1⊿x1－m1⊿x1)＋(M2⊿x2－m2⊿x2)＋…＋(Mn⊿xn－mn⊿xn)
=(M1－m1) ⊿x1＋(M2－m2) ⊿x2＋…＋(Mn－mn) ⊿xn
=ω1 ⊿x1＋ω2 ⊿x2＋…＋ωn ⊿xn
=右辺
定義：細分
[杉浦『解析入門I』212; 吹田新保『理工系の微分積分学』103.]
・閉区間 Iの二つの分割⊿、⊿' があって、⊿の分点はすべて、⊿'の分点でもあるとき、⊿'は⊿の細分であるという。
⊿≦⊿'と記す。
・細分してゆくほど、不足和は大きくなり、過剰和は小さくなる。
すなわち、⊿≦⊿'なら、s[⊿]≦s[⊿']、S[⊿]≧S[⊿']。
定義：下積分lower integral、上積分upper integral
[杉浦『解析入門I』213; 吹田新保『理工系の微分積分学』103.]
分割⊿の採り方によって、閉区間 Iにおけるf(x) の不足和s[⊿]・過剰和S[⊿]の大きさは変わってくる。
特に、「細分」でみたように、分割⊿を細分して行くほど、不足和s[⊿]は大きくなり、過剰和S[⊿]は小さくなる。
このような不足和s[⊿]の上限を、閉区間 Iにおけるf(x) の下積分と呼び、sで表す。
過剰和S[⊿]の下限を、閉区間 Iにおけるf(x) の上積分と呼び、Sで表す。
すなわち、閉区間 Iの分割全体の集合をDと表すと、
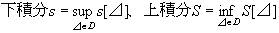
定理：以上の基本概念間の関係について
[杉浦『解析入門I』213; 吹田新保『理工系の微分積分学』102-5; 高木『解析概論』91-97..]
Iを閉区間 [a,b]、f(x)をI上の有界な関数とする。
1. Iにおけるfの上限をM、下限をmと書くと、
m ( b－a )≦s[⊿]≦S[⊿]≦M( b－a )
2. ⊿≦⊿'なら、s[⊿]≦s [⊿'] ≦S[⊿'] ≦S[⊿]
3. 任意の二つの分割⊿、⊿’に対し、s[⊿]≦S[⊿']
4. s≦S.
5. g≦fならば、s(g)≦s(f)、S(g)≦S(f)
6. f(x)のIkにおける振動量は、不足和・過剰和との間に以下の関係が成り立つ
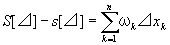
(1:証明)[杉浦『解析入門I』213;高木『解析概論』91;]
f(x)を閉区間I=[a,b]上の有界な関数とする。
Iにおけるfの上限をM、下限をm、
閉区間Iの分割⊿によって生じた各小区間Ik (k=1,2,…,n)でのfの下限をm k、上限をMkとおく。
また、各小区間Ikの長さを⊿xkとおく。
すべての各小区間Ik (k=1,2,…,n)において、m≦m k≦Mk≦M
よって、すべての各小区間Ik (k=1,2,…,n)において、
m⊿xk≦m k⊿xk≦Mk⊿xk≦M⊿xk (⊿xk >0だから)
ゆえに、
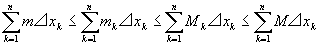
最左辺=mΣ⊿xk =m(b－a)、最右辺= MΣ⊿xk =M(b－a)、過剰和・不足和の定義より、
m ( b－a )≦s[⊿]≦S[⊿]≦M( b－a )
図：m ( b－a )≦s[⊿]
図： S[⊿]≦M( b－a )
(2:証明)
(3:証明) [杉浦『解析入門I』214; 吹田新保『理工系の微分積分学』103. を参照せよ。]
(4:証明) [杉浦『解析入門I』214; 吹田新保『理工系の微分積分学』103. を参照せよ。]
(5:証明) [杉浦『解析入門I』214を参照せよ。]
定理：ダルブーDarbouxの定理
fを閉区間 Iの有界関数とし、Iの分割⊿を考える。
このとき、閉区間Iの分割⊿を限りなく細かくしていくと、
分割⊿の取り方(つまり、区間Iをn個の小区間にわける際の分点のとりかた)によらず、
Iにおけるfの過剰和S[⊿]は上積分Sに収束し、Iにおけるfの不足和s[⊿]は下積分sに収束する。
これを記号で表すと、
|⊿|→0のとき、S[⊿]→S、s[⊿]→s
あるいは、
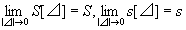
※ε-δ法による極限定義を用いて正確に書くと、
任意の（どんな）正の実数εに対して（でも）、
「 0＜|⊿|＜δ ならば
任意の(分点の取りかたで作れる)分割⊿に対して、
| S[⊿]－S|＜ε、 |s[⊿]－s|＜ε
を成り立たせる、ある正の実数δが存在する」
となる。上積分・下積分の定義から、常にS≦S[⊿], s[⊿]≦s なので、絶対値をはずして書くと、
任意の（どんな）正の実数εに対して（でも）、
「 0＜|⊿|＜δ ならば
任意の(分点の取りかたで作れる)分割⊿に対して、
0≦S[⊿]－S＜ε、0≦s－s[⊿]＜ε
を成り立たせる、ある正の実数δが存在する」
となる。移項して、不等式を変形すると、
任意の（どんな）正の実数εに対して（でも）、
「 0＜|⊿|＜δ ならば
任意の(分点の取りかたで作れる)分割⊿に対して、
S≦S[⊿]＜S+ε、s－ε＜s[⊿]≦s
を成り立たせる、ある正の実数δが存在する」
Cf.スチルチェス積分ではダルブーの定理は成立しない。
(証明)
杉浦『解析入門I』214-216; 吹田新保『理工系の微分積分学』104.
を参照せよ。
定理：可積分条件
以下の命題(1)～(5)は、同値である。
※これらはダルブーの定理を用いて可積分の定義を言い換えたものになっている。
Cf.スチルチェス積分では、
命題(1)-(3)が同値、命題(4)-(5)が同値だが、命題(1)-(3)と命題(4)-(5)は同値ではなくなる。
fを閉区間I上の有界な関数とする。
命題(1) fはI上リーマン可積分。
命題(2) 閉区間Iの分割⊿を限りなく細かくしていくと、
分割⊿の取り方(つまり、区間Iをn個の小区間にわける際の分点のとりかた)によらず、
Iにおけるfの(過剰和－不足和)はゼロに収束する。
すなわち、|⊿|→0のとき、S[⊿]－s[⊿]→0
あるいは、
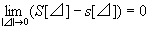
(記号|⊿|→0は、分割の幅が→0なら、そのようなすべての分割の取り方に対して、という意味。
ダルブーの定理を参照のこと。)
※ε-δ法による極限定義を用いて正確に書くと、
任意の（どんな）正の実数εに対して（でも）、
「 0＜|⊿|＜δ ならば
任意の(分点の取りかたで作れる)分割⊿に対して、
| S[⊿]－s[⊿]|＜ε
を成り立たせる、ある正の実数δが存在する」
となる。ここでつねにs[⊿]≦S[⊿]であるから（∵）、絶対値を外して書くと、
任意の（どんな）正の実数εに対して（でも）、
「 0＜|⊿|＜δ ならば
任意の(分点の取りかたで作れる)分割⊿に対して、
0≦S[⊿]－s[⊿]＜ε
を成り立たせる、ある正の実数δが存在する」
となる。
命題(3)リーマンの可積分条件
閉区間Iの分割⊿によって生じた各小区間Ik (k=1,2,…,n) におけるfの振幅をωkと置く。
分割⊿を限りなく細かくしていくと、
分割⊿の取り方(つまり、区間Iをn個の小区間にわける際の分点のとりかた)によらず、
小区間Ikの幅とそこでの振幅との積(⊿xk・ωk)をk=1からnまで足し合せた和は0に収束する。
すなわち、
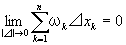
※利用例：単調関数は可積分、可積分な関数の積も可積分、積分の三角不等式、。
命題(4)ダルブーの可積分条件 上積分S=下積分s
命題(5) 任意のε>0に対し、
S[⊿]－s[⊿]＜ε
すなわち、
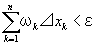
を満たすIの分割⊿が存在する。
(2:証明) (1)⇒(2)[杉浦『解析入門I』217;. を参照せよ。]
(3:証明) (2)⇔(3)[杉浦『解析入門I』217を参照せよ。]
小区間の振幅ωk 、過剰和S[⊿] 、不足和s[⊿])の定義から、
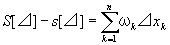
が成立する故に。
(4:証明)
(1)⇔(4)[吹田新保『理工系の微分積分学』104-5.]
(4)⇒(1) [杉浦『解析入門I』217; を参照せよ。]
(5)⇒(4) [杉浦『解析入門I』218; を参照せよ。]
(5:証明) [杉浦『解析入門I』218; を参照せよ。]
定理：閉区間Ｉ[a,b]上の単調関数は（無数の点で不連続でも）Ｉ上積分可能
[杉浦『解析入門I』218; 吹田新保『理工系の微分積分学』106;
高木『解析概論』定理32(p.96.)証明付;小平『解析入門I』158証明ナシ]
証明1：リーマンの可積分条件の利用
[杉浦『解析入門I』218; 吹田新保『理工系の微分積分学』』106.]
fは閉区間Ｉ[a,b]上の単調増加関数、⊿は、Iの任意の分割であるとする。
また、分割⊿によってできたn個の小区間を、Ik (k=1,2,…,n)、それぞれの幅を⊿xkで表し、
分割の幅を|⊿|で、Ikにおける振幅をωkで表す。
・ fは単調増加関数であるから、各小区間の振幅の和は、区間全体の振幅に等しくなる。
すなわち、Σωk = f(b)－f(a) …①
・
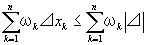∵meshの定義：|⊿| = max⊿xk
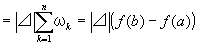∵①
ゆえに、
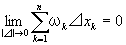
となり、可積分条件を満たす。
証明：一様連続性、リーマンの可積分条件の利用
[杉浦『解析入門I』227; 吹田新保『理工系の微分積分学』106.]
fは閉区間Ｉ[a,b]上の連続関数、⊿は、Iの任意の分割であるとする。
また、分割⊿によってできたn個の小区間を、Ik (k=1,2,…,n)、Ikそれぞれの幅を⊿xkで表し、
分割の幅を|⊿|で、Ikにおける振幅をωkで表す。
・定理より、閉区間 I[a,b]上の連続関数は一様連続である。
すなわち、
任意の正数εを決めると、それに応じて、点x0∈Iの選び方に関わり無く、
| f(x)－f(x0)|＜ε （ | x－x0| ＜ δ、 x,x0∈I ）…①
を満たす「ある」正数δが存在する。
・①を満たす正数δよりも、meshが細かい分割、
すなわち、|⊿|＜δとなるような任意の分割⊿を考える。
すると、小区間Ik (k=1,2,…,n)に含まれる任意の2点 xk , x k 0について、
| xk － x k 0|≦⊿xk≦|⊿|＜ δ、 x,x0∈ Ik
ゆえに①より、
| f( xk )－f( x k 0 )|＜ε
これと、Ikにおける振幅がωk=sup| f( xk )－f( x k 0 )|となることから、
ωk≦ε …②←なぜ等号？わからないが、どちらのテキストも等号付。
・|⊿|＜δとなるような（|⊿|＝δよりも細かい）任意の分割⊿から生じた
小区間の振幅ωk(k=1,2,…,n)を考えると、
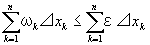∵②
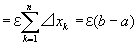…③
が成り立つ。
・以上を整理すると、
[手順1]任意の正数εを決める、
[手順2]それに応じて、①を満たす「ある正数」δが存在する。(一様連続だから)
[手順3]そのδよりも細かいmeshの分割では、
小区間の振幅が、最初に決めたε以下になり(②)、
ゆえに、Σωk⊿xk≦ε( b-a ) （③）も成り立つ。
ということだから、最初に、任意の正数εを小さくすれば、Σωk⊿xkは、どこまでも小さく出来る。
S[⊿]－s[⊿]＝Σωk⊿xkだから、（∵）
③から、
任意のε(b-a)＞０にたいして
S[⊿]－s[⊿]＜ε(b-a)を満たすIの分割⊿が存在するということになり、
可積分条件命題５を満たす。
定理：不連続点をもつ関数の可積分条件(1)〔十分条件〕
f(x)は閉区間 [a,b]上の有界な関数であるとする。
f(x)が閉区間 [a,b]上に、有限個数の不連続点しかもたないならば、
（有限個の点を除いてすべて連続ならば）
f(x)は閉区間 [a,b]で積分可能。
[高木『解析概論』p.96.、小平『解析入門I』158.]
(証明) 高木『解析概論』p.96.をみよ。
定理：不連続点をもつ関数の可積分条件(2)
f(x) は閉区間 [a,b]上の有界な関数であるとする。
f(x) が閉区間 [a,b]上に、不連続点を含む区間の長さの合計を限りなく小さくできるならば、
f(x) は積分可能
[高木『解析概論』p.96.、小平『解析入門I』158.]
〔証明〕
本質的だが、ここでは省略。
測度論とルベーグ積分から入るとよい。
定理：
高橋『経済学とファイナンスのための数学』79ページには、
「閉区間[a,b]上で有界な関数は積分可能」とあるが、
高木『解析概論』p.96.、小平『解析入門I』158.によれば、
この高橋一『経済学とファイナンスのための数学』の記述は間違い。
正しくは、「閉区間Iにおいて、f(x)が有限個数の不連続点を持ち、有界ならば、積分可能」ということらしい。
[注意1]で「もちろん有界だけでは積分可能ではない。」として、高木は例まで示している。
無数の不連続点をもつ関数の積分を考えるには、ルベーク積分論を勉強したほうがよいらしい。
（reference）
日本数学会編集『岩波数学辞典（第三版）』 岩波書店、1985年、202項積分法(pp.520-525)→リーマン積分、204項積分論(pp.530-533)→ルベーク積分。
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.102-106.
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.75-79.
小平邦彦『解析入門I』 (軽装版)岩波書店、2003年 pp.153-158。あらかじめ閉区間上の連続関数に限定して議論を進めている。
杉浦光夫『解析入門I』東京大学出版会、1980年、pp.205-229: n次元一般での定義;229-247:1変数関数の積分に特殊な性質（原始関数、…）。
高木貞治『解析概論:改訂第3版』岩波書店、1983年、p. 91-97.
青本和彦『岩波講座現代数学への入門：微分と積分1』岩波書店、1995年、122-126.軽く説明。
高橋陽一郎『岩波講座現代数学への入門：微分と積分2』 岩波書店、1995年、pp.1-11:単関数を用いてかなり厳密（ルベーク積分までは行かない）；pp.115-117。
矢野健太郎・田代嘉宏『社会科学者のための基礎数学 改訂版』裳華房、1993年、pp.106-9.
和達三樹『理工系の数学入門コース1:微分積分』岩波書店、1988年、pp.88-91. あらかじめ閉区間上の連続関数に限定して議論を進めている。
神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、pp.328-334.
小形正男『理工系数学のキーポイント7:多変数の微分積分』岩波書店、1996、87-89.