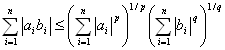凸関数 convex function
: トピック一覧
・定義:凸集合
・定義:凸関数(下に凸)/凹関数(上に凸)
・定理:凸性と微分/凹性と微分/凸不等式・Jensen(ジェンセン・イェンセン)の不等式/相加相乗平均不等式/Hölder (ヘルダー)の不等式
定義:凸集合 convex set
[ 高橋『経済学とファイナンスのための数学』p.67; 奥野鈴村『ミクロ経済学』pp.265-266]
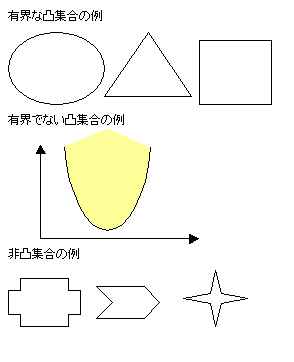
・「集合Aは凸集合である」とは、
集合Aに含まれる任意の2点を含む線分が、必ず集合Aに含まれるということ。
・すなわち、
「集合Aは凸集合である」とは、
n次元数ベクトルx,x' に対して、
x,x'∈A ⇒ {αx+(1−α) x'|α∈R, 0≦α≦1 }⊂A
が成立するということ。
※へこみがない図形をイメージせよ。
定理:凸集合の分離定理・分離超平面の定理 separating hyperplane theorem
[ 高橋『経済学とファイナンスのための数学』p.67; 奥野鈴村『ミクロ経済学』pp.268-270]
定義:凸関数(下に凸な関数) convex function
[高橋『経済学とファイナンスのための数学』67;奥野鈴村『ミクロ経済学』273;小平『解析入門I』138-140。]
【おおまかな考え方】
関数のグラフの上方が凸集合になれば、
すなわち、関数のグラフからどんな2点を選んで線分をつくっても、関数のグラフよりも上方にくれば、
その関数を凸関数と呼ぶ。
【きっちり定義すると】
f (x) が「閉区間Iで凸関数である」「閉区間Iで凸である」とは、
Iに属す2点x1,x2と、実数0≦α≦1を、どのようにとっても常に、
f (αx1+(1−α) x2 )≦αf (x1)+(1−α) f (x2 )
が成立することをいう。
また、
f (x) が「閉区間Iで狭義に凸 strictly convex である」
「閉区間Iで強い意味で凸 convex in the strong sense である」とは、
Iに属す2点x1,x2と、実数0≦α≦1を、どのようにとっても常に、
f (αx1+(1−α) x2 )<αf (x1)+(1−α) f (x2)
が成立することをいう。
【解説】
[小平『解析入門I』138]
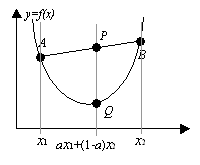
関数y =f (x)のグラフから2点A( x1, f (x1) ),B( x2, f (x2) )を選ぶ。
すると、線分AB上の任意の点Pの座標は、
任意のα(0≦α≦1)を用いて、
P( x2−α(x2−x1),f (x2)−α( f (x2)− f (x1) )
すなわち、
P(αx1+(1−α)x2,αf (x1)+ (1−α) f (x2) )
→もしわからなければ、
『高等学校数学I新訂版』啓林館
第6章平面図形と式・第2節平面上の座標「2点PQをm:nに分ける点の座標」(p.156)
を見よ。.
この点Pと同一x座標のy =f (x) 上の点Qの座標は、当然、
Q(αx1+(1−α)x2, f ( αx1+(1−α)x2 ) )
線分ABがグラフより上にあるということは、
線分AB上の任意の点Pが、同一x座標のy =f (x) 上の点Qより上にあるということに他ならない。
さらに、このことは、
[線分AB上の任意の点Pのy座標]≧[この点Pと同一x座標のy =f (x) 上の点Qのy座標]
すなわち、
任意のα(0≦α≦1)に対して、
f (αx1+(1−α)x2 )≦αf (x1)+(1−α)f (x2)
が成り立つことに他ならない。
定義:凹関数(上に凸な関数) concave function
[高橋『経済学とファイナンスのための数学』p.67; 奥野鈴村『ミクロ経済学』273;小平『解析入門I』138-140。]
【おおまかな考え方】
関数のグラフの下方が凸集合になれば、その関数は凹関数である。
すなわち、
関数のグラフからどんな2点を選んで線分をつくっても、関数のグラフよりも下方にくれば、
その関数を凹関数と呼ぶ。
【きっちり定義すると】
f (x) が「閉区間Iで凹関数である」「閉区間Iで凹である」とは、
Iに属す2点x1,x2と、実数0≦α≦1を、どのようにとっても常に、
f (αx1+(1−α) x2 )≧αf (x1 )+(1−α) f (x2 )
が成立することをいう。
また、
f (x) が「閉区間Iで狭義に凹 strictly concave である」
「閉区間Iで強い意味で凹 concave in the strong sense である」とは、
Iに属す2点x1,x2と、実数0≦α≦1を、どのようにとっても常に、
f (αx1+(1−α) x2 )>αf (x1 )+(1−α) f (x2 )
が成立することをいう。
※f (x) が凹(あるいは狭義に凹)であることは、
−f (x) が凸(あるいは狭義に凸)であることに他ならない。
【解説】 [小平『解析入門I』138]
凸関数の定義についての解説を見よ。
定理:凸と微分の関係
[吹田新保『理工系の微分積分学』57-58;小平『解析入門I』138-140。]
1.閉区間Iで連続、Iの内部で微分可能な関数f (x)が、
閉区間Iで凸であるための必要十分条件は、
導関数f ' (x) がI内部で増加であることである。
導関数 f ' (x) がIで狭義増加であるならば、
f (x) は、閉区間Iで狭義に凸である。
2.閉区間IでC2級である関数f (x)が、
閉区間Iで凸であるための必要十分条件は、
第二次導関数f '' (x) がIで、f '' (x)≧0となることである。
第二次導関数f '' (x) がIで、f '' (x)>0となるならば、
f (x) は、閉区間Iで狭義に凸である
3. 関数f (x)が微分可能な凸関数であるとき、
曲線y= f (x)はその曲線上の接線の下側にはでない。
(証明) [吹田新保『理工系の微分積分学』57-58;小平『解析入門I』138-140。]
定理:凹と微分の関係
[小平『解析入門I』138-140。]
1.閉区間Iで連続、Iの内部で微分可能な関数f (x) が、
閉区間Iで凹であるための必要十分条件は、
導関数f ' (x) がI内部でつねに減少であること。
導関数f ' (x) がIでつねに狭義減少であるならば、
f (x) は、閉区間Iで狭義凹。
2.閉区間IでC2級である関数f (x)が、
閉区間Iで凸であるための必要十分条件は、
第二次導関数f '' (x) がIでつねに、f '' (x)≧0となることである。
第二次導関数f '' (x) がIでつねに、f '' (x)>0となるならば、
f (x) は、閉区間Iで狭義に凸である
定理:凸不等式・Jensenの不等式(1)
[吹田新保『理工系の微分積分学』58; 高橋『経済学とファイナンスのための数学』p.89;]
f (x) は、区間Iで凸とする。
任意の数列{x1, x2, …, xn} ∈Iと、
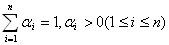
を満たす正数列{α1,α2, …,αn }に対し、
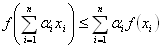
が成り立つ
f (x) が閉区間Iで狭義に凸であるならば、
等号は、 x1= x2= …= xn のときのみ成り立つ。
(証明) [吹田新保『理工系の微分積分学』58]
定理:凸不等式・Jensenの不等式(2)積分版
[高橋『経済学とファイナンスのための数学』90;]
f (x) は、区間Iで凸とする。ψ(x) は、積分可能な関数であるとする。
このとき、
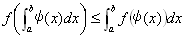
が成り立つ
(証明) [吹田新保『理工系の微分積分学』58]
定理:相加相乗平均不等式
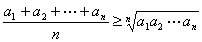
(等号は、 a1= a2= …= an のときに限る)
(証明) [吹田新保『理工系の微分積分学』59] 指針:凸関数 f (x)=− log x に、凸不等式を適用して導出。
定理:ヘルダーHölderの不等式
1/p+1/q=1, p,q>1のとき、
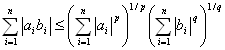
(証明) [吹田新保『理工系の微分積分学』59]
(reference)
高橋一『経済学とファイナンスのための数学』新世社、1999年、pp.67-70定義;p.89:Jensen不等式.
奥野正寛、鈴村興太郎『ミクロ経済学』岩波書店、1985年、pp.265-270;273-274。
小平邦彦『解析入門I』岩波書店、2003年 pp.138-140。
吹田・新保『理工系の微分積分学』学術図書出版社、1987年。pp.56-59.
高橋陽一郎『岩波講座現代数学への入門:微分と積分2』 岩波書店、1995年、pp.10-11:Jensenの不等式。
高木貞治『解析概論 改訂第三版』岩波書店、1983年、p. 52-54.
杉浦光夫『解析入門』岩波書店、1980年、p.76;102.
吉田耕作・栗田稔・戸田宏『平成元年3/31文部省検定済高等学校数学科用 高等学校 微分・積分 新訂版』啓林館、pp.85-86.
小林道正『Mathematicaによる微積分』朝倉書店、1995年、pp.36-40.神谷和也・浦井憲『経済学のための数学入門』東京大学出版会、1996年、pp.118-120;281.
Chiang, Fundamental Methods of Mathematical Economics: Third Edition, McGraw Hill,1984,pp.337-352.
Fischer,Emanuel.Intermediate Real Analysis(Undergraduate Texts in Mathematics),Springer-Verlag New York Heidelberg Berlin,1983, pp.340-377.
本格的な多変数関数の凸解析については、以下を参照せよ。
Rockafellar, Convex Analysis, Princeton UP, 1970.
布川昊,谷野哲三,中山弘隆『線形代数と凸解析』コロナ社、1991年。