定義:
n変数関数が点Aで連続はじめに
読むべき
定義
「
n変数関数 f は、点A(a1,a2,…,an )で連続であるcontinuous」とは、次の3条件がすべて満たされることを言う。
(1) f (A)、すなわち、f (a1,a2,…,an ) が定義されていること
(2) P→Aで、f (P)が収束すること。
つまり、
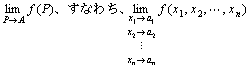
が存在すること。
(3) f (P)→f (A)(P→A)
つまり、
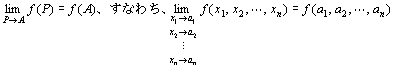
が成立すること。
※上記条件の一つでも満たされていないとき、
f (P)は点Aで不連続であるdiscontinuous、
ないしは、f (x1,x2,…,xn)は点(a1,a2,…,an )で不連続であるという。
cf
.点集合上連続/一様連続性[
具体例]1変数関数の連続性/2変数関数の連続性[
一般化]実数値関数/ベクトル値関数/距離空間上の写像/位相空間上の写像[
文献]杉浦『解析入門I』定義5(p.55-56);
髙木『解析概論』10連続函数(p.26)
吹田新保『理工系の微分積分学』6章§2(II)(p.160)
舞台設定
厳密には、
「
Step1: n次元空間Rnを用意する。
* n次元空間Rnとは、 実数をn個並べた組 (x1,x2,…,xn ) をすべてあつめた集合。
実n次元数ベクトルをすべて集めた集合でもある。
Step2: n次元空間Rnに距離dを定めて、距離空間(Rn,d)を設定。
*普通は、 n次元空間Rnにユークリッド距離を与えたユークリッド空間を考える。
Step3: n次元空間Rn上の点集合のひとつを選んで、集合Dと名づける。つまり、「D⊂Rn」
*Dは、「実n次元数ベクトルの集合」とも呼べる。
Step4: n次元空間Rn上の点集合Dで定義された n変数関数 f を用意。
つまり、f : D→R (D⊂Rn )、z=f(P) ( z∈R, P∈Rn ) 、z=f(x1,x2,…,xn ) ( z∈R, (x1,x2,…,xn )∈Rn )
*fは「Dに属す各実n次元数ベクトルから実数への対応付け」だとも言える。
Step5:「 n次元空間Rnの点集合D」に属す動点を、P= (x1,x2,…,xn )と名づける。
「 n次元空間Rnの点集合D」に属す定点を、A = (a1,a2,…,an )と名づける。
つまり、「P, A∈D⊂Rn」
*P, Aは、「Dに属す実n次元数ベクトル」といってもよい。
厳密な
定義
ε
「
n変数関数f (P)すなわちf (x1,x2,…,xn)は、点A(a1,a2,…,an )で連続であるcontinuous」とは、
任意の正数εに対して、ある正の実数δが存在して、
「 d ( P, A )<δ ならば、d ( f (P), f (A) )<ε 」
を成り立たせる、ということ。
この定義を、論理記号で表せば、
(∀ε>0)(∃δ>0)(∀P∈Rn)( d ( P, A )<δ⇒ d( f (P), f (A) )<ε)
* d ( P, A )は、 n次元空間Rn上での点Pと点Aとの距離を、
d ( f (P), f (A) )は、R上のf (P)とf (A)との距離| f (P)-f (A)|を表す。
*
「P→Aのときf(P)が収束する」の定義では、0<d( P, A )<δ であった。
つまり、関数の「極限」では、P=Aを除外して考えたが、
「連続」ではP=Aを除外しないことになる。
[
文献]髙木『解析概論』10連続函数(p.26);
吹田新保『理工系の微分積分学』6章§2(II)(p.160)
杉浦『解析入門I』命題6.5-b(p.55-56);
ルディン『現代解析学』4.5(p.83):一般の距離空間上で。
松坂『集合・位相入門』4章§1-G(p.149);
小平『解析入門Ⅱ』
§6.4(p309):2変数関数と同じとあるだけ;
※ユークリッド距離が定められたユークリッド空間
Rnにおける連続概念n変数関数f (P)= f (x1,x2,…,xn)、すなわち「『 n次元空間Rnの部分集合』から『実数体R』への写像」を扱う際には、
特別な目的がない限り、
n次元空間Rn上の距離をユークリッド距離で定めて、 n次元空間Rnをユークリッド空間Rnとし、
実数体Rの距離をユークリッド距離で定めて、Rを1次元ユークリッド空間Rとする設定のもとで
考えるのが普通。
この設定下では、
d (f (P), f (A) )=| f (P)-f (A)|=| f (x1,x2,…,xn )-f (a1,a2,…,an )|
だから、
「f (P)=f (x1,x2,…,xn)は、点A(a1,a2,…,an )で連続である」の定義は、具体的には
┌任意の(どんな)正の実数εに対して(でも)、ある正の実数δが存在して、
| 「
| ならば | f (x1,x2,…,xn )-f (a1,a2,…,an )|<ε」
└を成り立たせる
(∀ε>0)(∃δ>0)(∀x1,x2,…,xn ∈R )
(
となる。
※
n次元数ベクトル空間の上に定義されたユークリッド空間Rnにおける連続概念Rnにベクトルの加法・スカラー乗法・自然な内積(標準内積)・ユークリッドノルム∥∥が定義されており、
Rnを実n次元数ベクトル空間・計量実ベクトル空間・ノルム空間として扱える場合、
任意の実n次元数ベクトルx, y∈Rnのユークリッド距離は∥x-y∥ と表せる。
このユークリッド距離を定義したユークリッド空間Rnのもとでは、
d ( P, A )=∥P-A∥
だから、
「f (P)すなわちf (x1,x2,…,xn)は、点A(a1,a2,…,an )で連続であるcontinuous」の定義は、
「任意の(どんな)正の実数εに対して(でも)、ある正の実数δが存在して、
『 ∥P-A∥<δ ならば | f (P)-f (A)|<ε』
を成り立たせる」
(∀ε>0)(∃δ>0)(∀P∈Rn )(∥P-A∥<δ⇒| f (P)-f (A)|<ε )
と表せる。
ただし、上記のPは、「点P (x1,x2,…,xn )」を表す実n次元数ベクトル(x1,x2,…,xn )、
上記のAは、「点A (a1,a2,…,an )」を表す実n次元数ベクトル(a1,a2,…,an )
である。
厳密な
定義
近傍
「
n変数関数f (P)すなわちf (x1,x2,…,xn)は、点A(a1,a2,…,an )で連続であるcontinuous」とは、
実数f (A)の任意の(どんな)「R上のε近傍 Uε( f (A) ) 」に対して(でも)、
ある「Rn上の点Aのδ近傍Uδ(A)」が存在して、
f ( Uδ(A) ) ⊂ Uε( f (A) )
を満たす
ということ。
この定義を別の表現でいうと、
任意の(どんな)正の実数εに対して(でも)、ある正の実数δが存在して、
「 f ( Uδ(A) ) ⊂ Uε( f (A) ) 」
すなわち「 (x1,x2,…,xn)∈Uδ(A) ならば、f (x1,x2,…,xn) ∈ Uε(f (A))」
を成り立たせる、
ということ。
この定義を、論理記号で表せば、
(∀ε>0)(∃δ>0)( f ( Uδ(A) ) ⊂ Uε(f (A)) )
(∀ε>0)(∃δ>0)(∀P∈Rn)( P∈Uδ(A) ⇒ f (P) ∈Uε(f (A)))
となる。
[
文献]杉浦『解析入門I』命題6.5-c(p.55-56);
斉藤『数学の基礎:集合・数・位相』3.4.16(p.90)
松坂『集合・位相入門』4章§1-G(p.149)
活用例
